Расчет напряжений в стержневой конструкции

ЗАДАНИЕ

на производственную практику

Студент: Фамилия Имя Отчество Группа: ПМ-343

Период практики: 26.06.2017 – 23.07.2017

База практики: юридическое название

Руководитель от базы практики: должность, ФИО

1. Тема работы

Моделирование задач теории упругости.

2. Основное содержание

2.1. Изучить теоретические основы теории упругости, в том числе использование дифференциальных уравнений в теории упругости.

2.2. Провести аналитический расчет изгиба балки с различными видами закреплений (консольное, шарнирное).

2.3. Смоделировать и рассчитать консольную балку и двухопорную балку с шарнирным закреплением в инженерном пакете ANSYS Mechanical.
2.4. Сравнить полученные результаты.

2.5. Смоделировать и рассчитать лопатку компрессора ГТД в ANSYS Mechanical под действием различных нагрузок: центробежная сила, давление набегающего потока. Сравнить результаты с допускаемыми значениями.

Список рекомендуемой литературы

3.1 Ландау Л.Д. и Лифшиц Е.М. Теория упругости. – Москва : Наука, 1987. – 246 с.

3.2 Феодосьев В.И. Сопротивление материалов. – М.: МГТУ им. Н.Э. Баумана, 2005. – 590с.

3.3 Справочное руководство ANSYS Mechanical 15.0.

Дата выдачи задания 27 июня 2017 г.

Дата окончания работы 20 июля 2017 г.

Руководитель от базы практики _________________ Фамилия И.О.

Руководитель от университета _________________ Ямилева А.М.

Содержание

Введение. 5

1. Теоретический материал. 6

1.1. Растяжение и сжатие. 6

1.2. Кручение. 8

1.3. Чистый изгиб. 10

1.4. Поперечный изгиб. 11

2. Расчет напряжений в стержневой конструкции. 14

2.1. Расчет на прочность и жесткость при деформации растяжения. 14

2.2. Расчет на прочность и жесткость при деформации кручения. 16

2.3. Расчет на прочность и жесткость при чистом изгибе. 18

2.4. Расчет на прочность и жесткость при поперечном изгибе. 19

3. Расчет напряжений в лопатке компрессора ГТД.. 21

Заключение. 22

Список литературы.. 23

Введение

При выполнении инженерных расчетов, связанных с анализом прочности конструкций, на практике используют как аналитические, так и численные методы. Однако аналитические расчеты позволяют получить решение задач для тел, имеющих достаточно простую геометрическую форму и схему нагружения. В то же время применение численных методов, к которым относятся методы конечных разностей, конечных элементов не ограничено ни сложностью геометрии тела, ни способами приложения нагрузок.

Целью данной работы является изучение основ теории упругости и приобретение навыков, необходимых для расчета простых нагружений стержневой конструкции и лопатки компрессора ГТД.

Теоретический материал

Растяжение и сжатие

Под растяжением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы.

Во всех поперечных сечениях стержня возникают нормальные силы N, равные P.

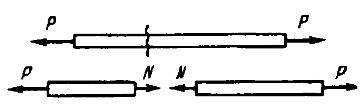
Рис.1.1.

Сжатие отличается от растяжения знаком силы N. При растяжении нормальная сила N направлена от сечения, а при сжатии – к сечению.

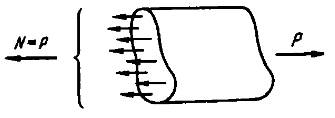
Рис.1.2.

Нормальная сила N является равнодействующей внутренних сил в сечении. Предположим, что для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет одним и тем же:

,

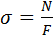где F - площадь поперечного сечения.

Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна l, то после нагружения она станет равной 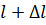. Величину 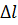называют абсолютным удлинением стержня.

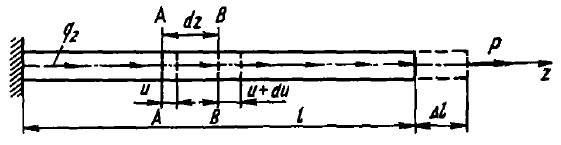
Рис.1.3.

Если стержень нагружен только силой P, то напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях; деформация 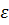по оси стержня остается одной и той же, равной своему среднему значению по длине :

.

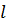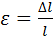Эта величина называется относительным удлинением стержня.

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

.

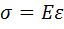Величина E представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода.

Абсолютное удлинение стержня переменного сечения на длине 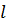будет равно

Если стержень нагружен только по концам и имеет постоянные размеры поперечного сечения F, то нормальная сила 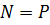не зависит от z и получаем:

.

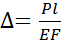Кручение

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент.

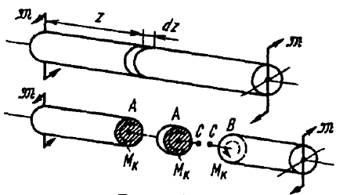
Рис.1.4.

При расчете стержня на кручение требуется определить напряжения и найти угловые перемещения в зависимости от внешних моментов.

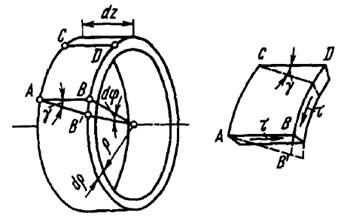
Рис.1.5.

Правое торцевое сечение кольца поворачивается при кручении относительно левого на угол 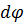. Образующая цилиндра поворачивается при этом на угол

.

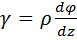Величину

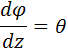
называют относительным углом закручивания. Это – угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.

По закону Гука для сдвига

,

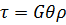где 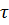– касательные напряжения, возникающие в поперечном сечении бруса.

Интеграл 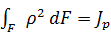представляет собой геометрическую характеристику и называется полярным моментом инерции сечения.Таким образом, 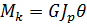. Произведение 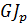называют жесткостью стержня при кручении.

Взаимный угол поворота сечений 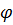можно определить:

,

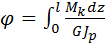где l – расстояние между сечениями, для которых определяют взаимный угол поворота .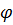

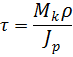
Таким образом, касательные напряжения в поперечном сечении распределены вдоль радиуса по линейному закону и имеют наибольшее значение в точках, наиболее удаленных от оси. При этом

.

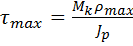Величина

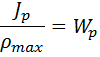
называется полярным моментом сопротивления.

Если стержень имеет сплошное круговое сечение, то

, ,

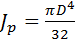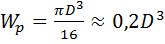где D – диаметр сечения.

Если же в стержне имеется внутренняя центральная полость диаметром d, то

, .

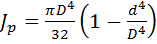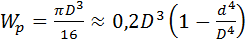Чистый изгиб

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты. Если изгибающий момент в сечении является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, изгиб называется чистым.

Образование деформаций при чистом изгибе можно рассматривать как результат поворота плоских поперечных сечений одно относительно другого.

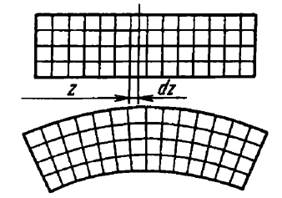
Рис.1.6.

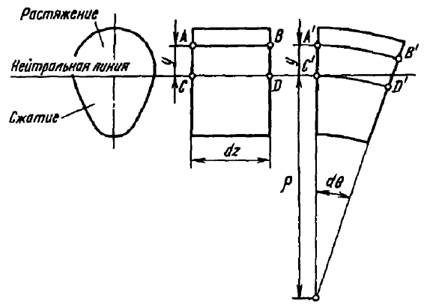
Рис.1.7.

Согласно закону Гука,

,

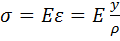где y – расстояние от рассматриваемого отрезка до нейтральной линии.

Таким образом, при чистом изгибе напряжения в поперечном сечении изменяются по линейному закону. Геометрическое место точек в сечении, удовлетворяющее условию 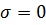, называется нейтральной линией сечения. Нейтральная линия перпендикулярна к плоскости кривизны изогнутого стержня.

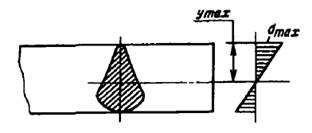
Рис.1.8.

Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии:

,

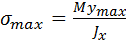где 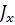– момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента.

Отношение 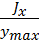называется моментом сопротивления сечения при изгибе и обозначается через :

.

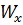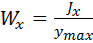Для стержня круглого сечения

, , .

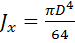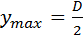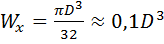Поперечный изгиб

В случае поперечного изгиба в сечении стержня возникают не только изгибающий момент, но и поперечная сила Q. Эта сила представляет собой равнодействующую распределенных сил, лежащих в плоскости сечения. Следовательно, в этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.

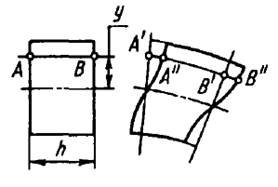
Рис.1.9.

Возникновение касательных напряжений 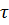сопровождается появлением угловых деформаций 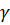. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом. Это значит, что при поперечном изгибе в отличие от чистого изгиба поперечные сечения не остаются плоскими.

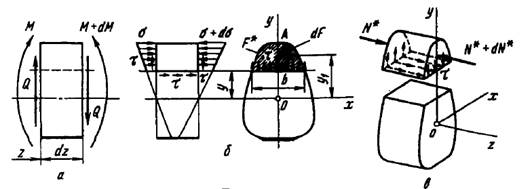
Рис.1.10.

Равнодействующая нормальных сил 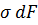в левом сечении в пределах заштрихованной площади 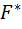равна

,

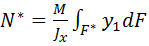где через 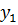обозначена текущая ордината площадки .

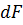Полученный интеграл представляет собой статический момент относительно оси x, который обозначим через 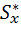. Тогда

.

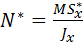В правом сечении нормальная сила будет другой:

.

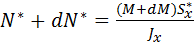В качестве первого приближения примем, что касательные напряжения распределены по ширине сечения b равномерно. Тогда

,

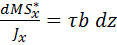откуда

.

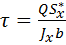Для стержня круглого сечения

.

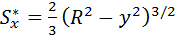Также,

,

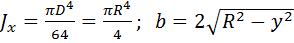откуда

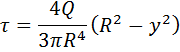
и

.

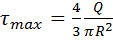Заключение

В данной работе изложены основные теоретические сведения по типам простых нагружений и рассмотрено их применение к решению некоторых задач раздела «Теория упругости».

Был проведен расчет напряженно-деформированного состояния стержневой конструкции при четырех видах нагружения, а также было достигнуто согласие между результатами аналитических расчетов и результатами, полученными с помощью инженерного пакета ANSYSMechanical.

Кроме того, полученные навыки решения базовых задач были применены к расчету напряжений в лопатке компрессора ГТД. Эксперименты показали, что при давлении на одну из сторон лопатки наибольшее напряжение сосредоточено в ее центральной области. Это связано со сложной формой исследуемого объекта. В случае кручения, максимальное напряжение распределено по краям верхней области лопатки.

Список литературы

1. Феодосьев В.И. Сопротивление материалов. – М.: МГТУ им. Н.Э. Баумана, 2005. – 590с.

2. Биргер И. А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие. – М.: Наука. Гл. ред. физ.-мат. лит., 1986. – 560 с.

3. Кравчук А.С., Смалюк А.Ф., Кравчук А.И. Лекции по ANSYS с примерами решения задач в пяти частях. – Минск: БГУ, 2013. – 193с.

ЗАДАНИЕ

на производственную практику

Студент: Фамилия Имя Отчество Группа: ПМ-343

Период практики: 26.06.2017 – 23.07.2017

База практики: юридическое название

Руководитель от базы практики: должность, ФИО

1. Тема работы

Моделирование задач теории упругости.

2. Основное содержание

2.1. Изучить теоретические основы теории упругости, в том числе использование дифференциальных уравнений в теории упругости.

2.2. Провести аналитический расчет изгиба балки с различными видами закреплений (консольное, шарнирное).

2.3. Смоделировать и рассчитать консольную балку и двухопорную балку с шарнирным закреплением в инженерном пакете ANSYS Mechanical.
2.4. Сравнить полученные результаты.

2.5. Смоделировать и рассчитать лопатку компрессора ГТД в ANSYS Mechanical под действием различных нагрузок: центробежная сила, давление набегающего потока. Сравнить результаты с допускаемыми значениями.

Список рекомендуемой литературы

3.1 Ландау Л.Д. и Лифшиц Е.М. Теория упругости. – Москва : Наука, 1987. – 246 с.

3.2 Феодосьев В.И. Сопротивление материалов. – М.: МГТУ им. Н.Э. Баумана, 2005. – 590с.

3.3 Справочное руководство ANSYS Mechanical 15.0.

Дата выдачи задания 27 июня 2017 г.

Дата окончания работы 20 июля 2017 г.

Руководитель от базы практики _________________ Фамилия И.О.

Руководитель от университета _________________ Ямилева А.М.

Содержание

Введение. 5

1. Теоретический материал. 6

1.1. Растяжение и сжатие. 6

1.2. Кручение. 8

1.3. Чистый изгиб. 10

1.4. Поперечный изгиб. 11

2. Расчет напряжений в стержневой конструкции. 14

2.1. Расчет на прочность и жесткость при деформации растяжения. 14

2.2. Расчет на прочность и жесткость при деформации кручения. 16

2.3. Расчет на прочность и жесткость при чистом изгибе. 18

2.4. Расчет на прочность и жесткость при поперечном изгибе. 19

3. Расчет напряжений в лопатке компрессора ГТД.. 21

Заключение. 22

Список литературы.. 23

Введение

При выполнении инженерных расчетов, связанных с анализом прочности конструкций, на практике используют как аналитические, так и численные методы. Однако аналитические расчеты позволяют получить решение задач для тел, имеющих достаточно простую геометрическую форму и схему нагружения. В то же время применение численных методов, к которым относятся методы конечных разностей, конечных элементов не ограничено ни сложностью геометрии тела, ни способами приложения нагрузок.

Целью данной работы является изучение основ теории упругости и приобретение навыков, необходимых для расчета простых нагружений стержневой конструкции и лопатки компрессора ГТД.

Теоретический материал

Растяжение и сжатие

Под растяжением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы.

Во всех поперечных сечениях стержня возникают нормальные силы N, равные P.

Рис.1.1.

Сжатие отличается от растяжения знаком силы N. При растяжении нормальная сила N направлена от сечения, а при сжатии – к сечению.

Рис.1.2.

Нормальная сила N является равнодействующей внутренних сил в сечении. Предположим, что для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет одним и тем же:

,

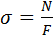где F - площадь поперечного сечения.

Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна l, то после нагружения она станет равной 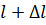. Величину 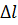называют абсолютным удлинением стержня.

Рис.1.3.

Если стержень нагружен только силой P, то напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях; деформация 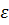по оси стержня остается одной и той же, равной своему среднему значению по длине :

.

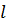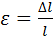Эта величина называется относительным удлинением стержня.

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

.

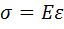Величина E представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода.

Абсолютное удлинение стержня переменного сечения на длине 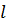будет равно

Если стержень нагружен только по концам и имеет постоянные размеры поперечного сечения F, то нормальная сила 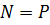не зависит от z и получаем:

.

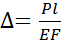Кручение

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент.

Рис.1.4.

При расчете стержня на кручение требуется определить напряжения и найти угловые перемещения в зависимости от внешних моментов.

Рис.1.5.

Правое торцевое сечение кольца поворачивается при кручении относительно левого на угол 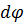. Образующая цилиндра поворачивается при этом на угол

.

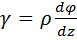Величину

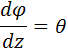
называют относительным углом закручивания. Это – угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.

По закону Гука для сдвига

,

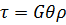где 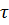– касательные напряжения, возникающие в поперечном сечении бруса.

Интеграл 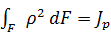представляет собой геометрическую характеристику и называется полярным моментом инерции сечения.Таким образом, 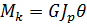. Произведение 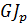называют жесткостью стержня при кручении.

Взаимный угол поворота сечений 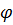можно определить:

,

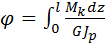где l – расстояние между сечениями, для которых определяют взаимный угол поворота .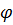

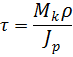
Таким образом, касательные напряжения в поперечном сечении распределены вдоль радиуса по линейному закону и имеют наибольшее значение в точках, наиболее удаленных от оси. При этом

.

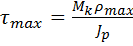Величина

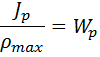
называется полярным моментом сопротивления.

Если стержень имеет сплошное круговое сечение, то

, ,

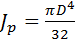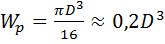где D – диаметр сечения.

Если же в стержне имеется внутренняя центральная полость диаметром d, то

, .

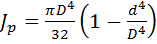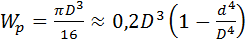Чистый изгиб

Под изгибом понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты. Если изгибающий момент в сечении является единственным силовым фактором, а поперечные и нормальные силы отсутствуют, изгиб называется чистым.

Образование деформаций при чистом изгибе можно рассматривать как результат поворота плоских поперечных сечений одно относительно другого.

Рис.1.6.

Рис.1.7.

Согласно закону Гука,

,

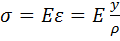где y – расстояние от рассматриваемого отрезка до нейтральной линии.

Таким образом, при чистом изгибе напряжения в поперечном сечении изменяются по линейному закону. Геометрическое место точек в сечении, удовлетворяющее условию 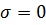, называется нейтральной линией сечения. Нейтральная линия перпендикулярна к плоскости кривизны изогнутого стержня.

Рис.1.8.

Максимальное напряжение при изгибе возникает в точках, наиболее удаленных от нейтральной линии:

,

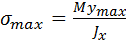где 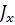– момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента.

Отношение 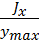называется моментом сопротивления сечения при изгибе и обозначается через :

.

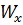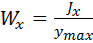Для стержня круглого сечения

, , .

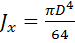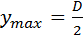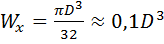Поперечный изгиб

В случае поперечного изгиба в сечении стержня возникают не только изгибающий момент, но и поперечная сила Q. Эта сила представляет собой равнодействующую распределенных сил, лежащих в плоскости сечения. Следовательно, в этом случае в поперечных сечениях возникают не только нормальные, но и касательные напряжения.

Рис.1.9.

Возникновение касательных напряжений 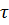сопровождается появлением угловых деформаций 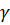. Поэтому, кроме основных смещений, свойственных чистому изгибу, каждая элементарная площадка сечения получает еще некоторые дополнительные угловые смещения, обусловленные сдвигом. Это значит, что при поперечном изгибе в отличие от чистого изгиба поперечные сечения не остаются плоскими.

Рис.1.10.

Равнодействующая нормальных сил 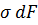в левом сечении в пределах заштрихованной площади 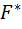равна

,

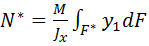где через 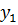обозначена текущая ордината площадки .

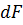Полученный интеграл представляет собой статический момент относительно оси x, который обозначим через 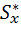. Тогда

.

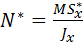В правом сечении нормальная сила будет другой:

.

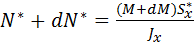В качестве первого приближения примем, что касательные напряжения распределены по ширине сечения b равномерно. Тогда

,

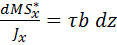откуда

.

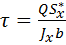Для стержня круглого сечения

.

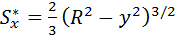Также,

,

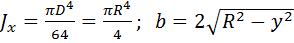откуда

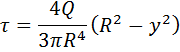
и

.

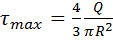Расчет напряжений в стержневой конструкции

В ходе исследования осуществляется расчет напряженно-деформированного состояния стержня постоянного поперечного сечения с помощью инженерного пакета ANSYS Mechanical. Рассматриваются два типа элементов: Beam188, служащий для моделирования стержневых конструкций, и Solid186, который применяется в расчетах твердотельных моделей (объемных и плоских).

Характеристики исследуемой модели:

Материал – сталь.

Коэффициент Пуассона .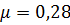

Модуль упругости первого рода .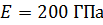

Длина стержня l = 1м.

Поперечное сечение – круг.

Радиус поперечного сечения R = 0.08м.