Общее Частное Базисное решения

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

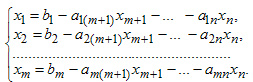
Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

• Базисное решение (вектор) называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
• Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена(имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена(имеет бесконечное множество решений).

Пример 1. Найти общее, базисное и какое-либо частное решение системы уравнений:

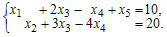
Решение:

1. Проверяем является ли система разрешенной?

• Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения.

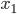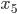• В нашем случае мы можем включить в набор разрешенных неизвестных из первого уравнения — и , а из второго уравнения только 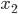. То есть набор может состоять из ( 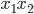) или ( ).

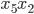3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор.

• допустим мы включили в набор неизвестные 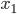и 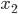, тогда общее решение будет выглядеть так:

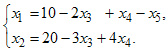
4. Находим частное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

• Пусть 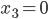, , 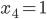, 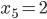тогда из общего решения находим:

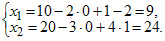
Ответ: частное решение (один из вариантов)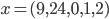

5. Находим базисное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

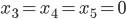• , то из общего решения получаем 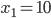, 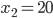и базисное решение: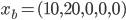

Элементарные преобразования линейных уравнений

Системы линейных уравнений приводятся к равносильным разрешенным системам с помощью элементарных преобразований.

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число, а остальные уравнения оставить без изменения, то получится система, равносильная данной. (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое, а все остальные уравнения оставить без изменения, то получится система, равносильная данной. (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число, а все остальные уравнения оставить без изменения, то получится система, равносильная данной.