Сравнение токов при различных видах КЗ

Анализируя полученные в п.2.4. формулы для расчёта тока КЗ при несимметричных повреждениях можно для простейшего случая сети с одним генератором получить соотношения между токами при различных видах КЗ:

Для любых повреждений имеют место соотношения

.

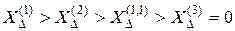Между токами прямой последовательности в месте повреждения имеет место следующая связь (так как ЭДС и сопротивления прямой последовательности одинаковы при различных повреждениях)

.

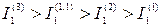Определим соотношения между полными токами.

Отношение тока двухфазного к трёхфазному КЗ

.

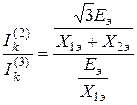Если 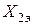близко по величине к 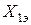, что соответствует удалённому КЗ или начальному значению тока КЗ в сети питаемой турбогенератором, то

.

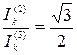Для установившихся значений токов КЗ вблизи генераторов 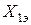обычно значительно больше 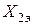, поэтому отношение 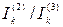может достигать 1,6. Таким образом, тепловой импульс при двухфазном КЗ может быть больше, чем при трёхфазном, и, следовательно, аппаратура и токоведущие части, расположенные в непосредственной близости к генератору, должны проверяться на тепловую устойчивость при трехфазном и двухфазном КЗ.

Для гидрогенератора в начальный момент времени 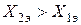, поэтому

.

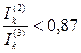Отношение тока однофазного КЗ к трёхфазному

.

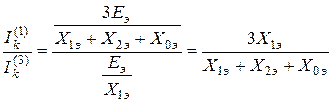В сетях 110 кВ часть нейтралей трансформаторов для уменьшения тока однофазного КЗ могут быть незаземлены. При этом в любой точке сети должно выдерживаться соотношение 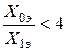, полагая, что 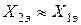получим отношение

.

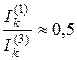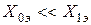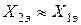При КЗ на шинах мощных электрических станций и подстанций имеет место соотношение , при отношение

.

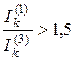Отношение тока двухфазного КЗ на землю к трёхфазному

.

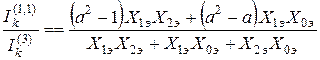Если 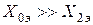, то данный вид замыкания соответствует двухфазному КЗ, т.е. 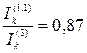. При равенстве 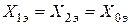имеем .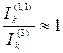

Замыкания на землю в электрических сетях с незаземлённой

Нейтралью

При однофазных замыканиях на землю в электрических сетях с незаземленной нейтралью в месте замыкания возникают только ёмкостные токи, обусловленные ёмкостью фаз относительно земли (рис. 2.21,а). При этом ток, как правило, не превышает 50 А, а само повреждение называется некоротким замыканием, а простым замыканием на землю.

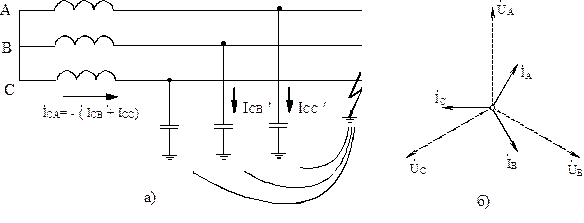
Рис.2.21. Однофазное замыкание на землю (а) и векторная диаграмма напряжений и токов в нормальном режиме

При замыкании происходит смещение нейтрали источника. На нейтрали появляется фазное напряжение, а напряжения неповреждённых фаз увеличиваются до линейного напряжения, т.е. в 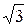раза. Это называется перекосом напряжений фаз относительно земли. Линейные напряжения остаются без изменения.

Перекос напряжений не распространяется через трансформаторы на другую электрическую ступень. Через автотрансформаторы, имеющие в отличие от трансформаторов помимо магнитной и электрическую связь между обмотками, перекос фаз может перейти с обмотки высшего напряжения на обмотку низшего, если нейтраль не заземлена. Поэтому нейтрали автотрансформаторов всегда заземляются, и, следовательно, они не применяются в сетях с изолированными нейтралями (в сетях с напряжением ниже 110 кВ).

В предшествующем замыканию режиме ёмкостные токи равны (рис.2.21,б)

,

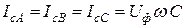где 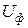- фазное напряжение.

При замыкании (рис.2.22)

, , .

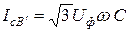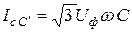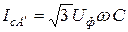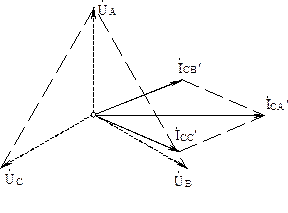
Рис.2.22. Векторная диаграмма напряжений и токов при однофазном замыкании на землю

Таким образом, ток в месте замыкания на землю, равен арифметической сумме ёмкостных токов фаз предшествующего режима. Система ёмкостных токов является неуравновешенной и поэтому ведёт себя так же, как и система нулевой последовательности. При значительной величине тока замыкания возникают условия для возникновения перемежающейся дуги, что может привести к перенапряжениям в сети, опасными для изоляции. Величина тока замыкания может быть уменьшена (скомпенсирована) с помощью реактора, включённого в нейтраль трансформатора.

КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 2

1. Назначение и сущность метода симметричных составляющих.

2. Основные уравнения метода симметричных составляющих.

3. Сопротивление электрических машин токам обратной последовательности.

4. Схемы замещения трансформаторов при протекании токов нулевой последовательности.

5. Сопротивление линий электропередачи токам нулевой последовательности.

6. Схемы замещения отдельных последовательностей.

7. Двухфазное короткое замыкание. Расчёт токов и напряжений. Построение векторных диаграмм.

8. Однофазное короткое замыкание. Расчёт токов и напряжений. Построение векторных диаграмм.

9. Двухфазное короткое замыкание на землю. Расчёт токов и напряжений. Построение векторных диаграмм.

10. Правило эквивалентности прямой последовательности.

11. Учёт активных сопротивлений в месте КЗ.

12. Распределение и трансформация токов и напряжений отдельных последовательностей.

13. Сравнение токов при различных видах КЗ.

14. Замыкания на землю в электрических сетях с незаземлённой нейтралью.

ЛЕКЦИЯ 13

ПРОДОЛЬНАЯ НЕСИММЕТРИЯ

Общие сведения

В трёхфазных сетях иногда сопротивления фаз оказываются различными, Это называется продольной несимметрией. Наиболее сильно несимметрия проявляется при обрыве проводов, а также при пофазном отключении электрооборудования однофазными выключателями. В данном разделе рассмотрены методы расчёта токов и напряжений при продольной несимметрии.

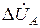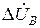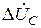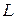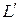В общем случае несимметрии во всех фазах включены различные сопротивления (рис.3.1, а), которые могут быть связаны между собой взаимоиндукциями. Падения напряжений на сопротивлениях в фазах обозначим , , . Вместо сопротивлений в схему могут быть включены ЭДС, соответствующие падениям напряжения на сопротивлениях (рис.3.1, б). Индексы и принято использовать для обозначения продольной несимметрии, аналогично как индекс 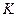для обозначения коротких замыканий, т.е. поперечной несимметрии.

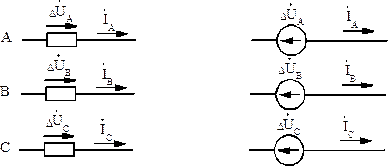
а) б)

Рис.3.1. Продольная несимметрия фаз

Используя метод симметричных составляющих напряжения 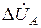, , 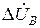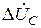можно разложить на симметричные составляющие и для особой фазы 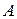составить схемы замещения прямой, обратной и нулевой последовательностей для участка энергосистемы, состоящего из двух систем 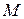и 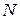(рис. 3.2).

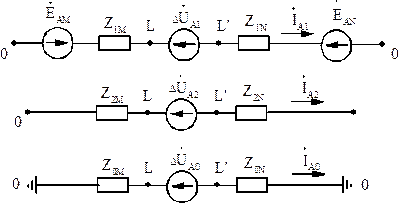
Рис.3.2. Схемы замещения при продольной несимметрии

Этим схемам соответствуют уравнения

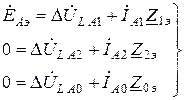, (3.1)

где , , , .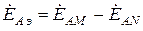

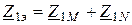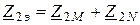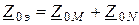Таким образом, напряжения прямой, обратной и нулевой последовательностей в месте продольной несимметрии появляются в результате разложения системы несимметричных векторов фазных напряжений на симметричные составляющие.

Расчёт токов и напряжений в случае продольной несимметрии может быть произведен путём решения системы уравнений (3.1). Система из трёх уравнений содержит 6 неизвестных. Поэтому для её решения используются три дополнительных уравнения исходя из граничных условий, зависящих от вида несимметрии. Далее рассматриваются два вида продольной несимметрии: разрыв одной и двух фаз.

Разрыв одной фазы

Рассмотрим разрыв особой фазы 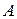(рис.3.3).

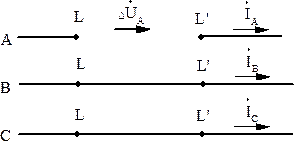
Рис.3.3. Разрыв фазы одной фазы

Этому случаю продольной несимметрии соответствуют граничные условия:

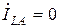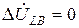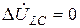, , . (3.2)

Эти условия аналогичны граничным условиям при двухфазном КЗ на землю, что обуславливает и аналогичные расчётные выражения.

Из системы уравнений (2.5) с учётом граничных условий (3.2) получим:

, , .

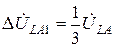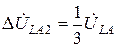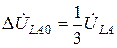Из системы уравнений (3.1)

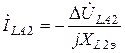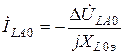, . (3.3)

Так как 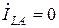, то

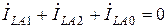. (3.4)

Подставив в (3.4) выражения (3.3), получим

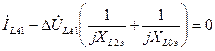
или

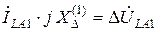, (3.5)

где 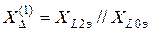(индекс 1 означает разрыв одной фазы).

Из первого уравнения (3.1) с учётом (3.5) получим формулу для вычисления тока прямой последовательности при продольной несимметрии

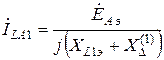. (3.6)

Формула (3.6) аналогична формуле для вычисления тока прямой последовательности при КЗ на основе правила эквивалентности прямой последовательности.

Используя соотношения между симметричными составляющими, получена комплексная схема замещения при разрыве одной фазы (рис. 3.4).

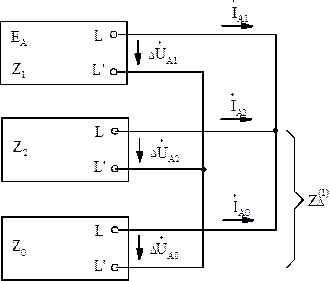
Рис.3.4. Комплексная схема замещения при разрыве одной фазы

Из комплексной схемы замещения находим токи обратной и нулевой последовательностей

,

.

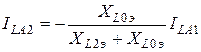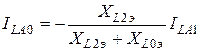Полные токи и напряжения получают путем суммирования векторов прямой обратной и нулевой последовательностей.

Разрыв двух фаз

Рассмотрим разрыв фаз 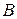и 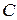(рис.3.5).

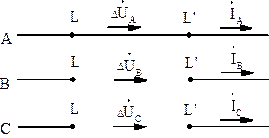
Рис.3.5. Разрыв двух фаз

Этому случаю продольной несимметрии соответствуют граничные условия:

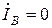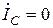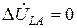, , . (3.7)

При этом граничные условия аналогичны граничным условиям при однофазном КЗ.

Из системы уравнений (2.3) с учётом граничных условий (3.7) получим:

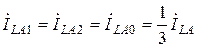, (3.8)

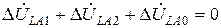. (3.9)

Сложим уравнения системы (3.1) с учётом (3.8) и (3.9) и после несложных преобразований найдем

,

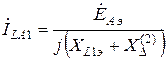где 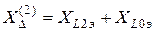(индекс 2 означает разрыв двух фаз).

Для тока в фазе 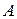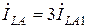. Разность фазных напряжений прямой последовательности в месте разрыва определяется путём сложения двух последних уравнений системы (3.1) с учётом (3.8) и (3.9)

.

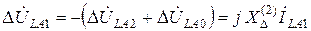Рис.3.6. Комплексная схема замещения при разрыве двух фаз

Используя соотношения между симметричными составляющими (3.8) и (3.9) построена комплексная схема при разрыве двух фаз (рис. 3.6).

Пример 3.1. Для схемы, приведенной на рис.3.7 построить комплексную схему замещения при разрыве одной фазы и двух фаз в начале линии.

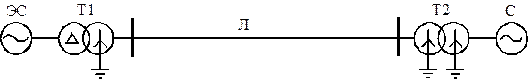
Рис.3.7. Схема участка энергосистемы

Требуемые схемы замещения приведены на рис.3.8 и 3.9 соответственно. Комплексные схемы замещения соответствуют особой фазе А.

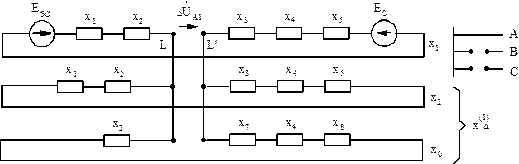
Рис.3.8.Схема замещения при разрыве одной фазы

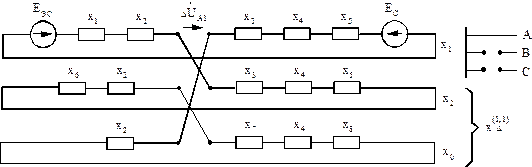
Рис.3.9.Схема замещения при разрыве двух фаз

Подобные схемы используются, как правило, для расчёта переходных электромеханических процессов, которые протекают сравнительно медленно (1-3 с). Поэтому для генератора задаются переходное сопротивление 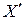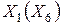(без учёта влияния демпферных контуров) и переходная ЭДС.

КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 3

1. Назначение и сущность метода симметричных составляющих.

2. Основные уравнения метода симметричных составляющих.

3. Разрыв одной фазы. Расчёт токов и напряжений.

4. Разрыв двух фаз. Расчёт токов и напряжений.

ЛЕКЦИЯ 14

ПРОДОЛЬНАЯ НЕСИММЕТРИЯ

Общие сведения

В трёхфазных сетях иногда сопротивления фаз оказываются различными, Это называется продольной несимметрией. Наиболее сильно несимметрия проявляется при обрыве проводов, а также при пофазном отключении электрооборудования однофазными выключателями. В данном разделе рассмотрены методы расчёта токов и напряжений при продольной несимметрии.

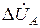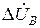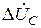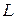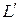В общем случае несимметрии во всех фазах включены различные сопротивления (рис.3.1, а), которые могут быть связаны между собой взаимоиндукциями. Падения напряжений на сопротивлениях в фазах обозначим , , . Вместо сопротивлений в схему могут быть включены ЭДС, соответствующие падениям напряжения на сопротивлениях (рис.3.1, б). Индексы и принято использовать для обозначения продольной несимметрии, аналогично как индекс 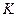для обозначения коротких замыканий, т.е. поперечной несимметрии.

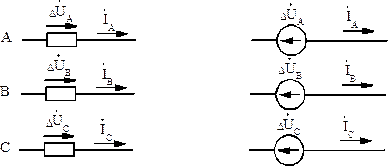
а) б)

Рис.3.1. Продольная несимметрия фаз

Используя метод симметричных составляющих напряжения 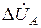, , 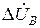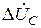можно разложить на симметричные составляющие и для особой фазы 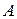составить схемы замещения прямой, обратной и нулевой последовательностей для участка энергосистемы, состоящего из двух систем 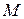и 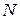(рис. 3.2).

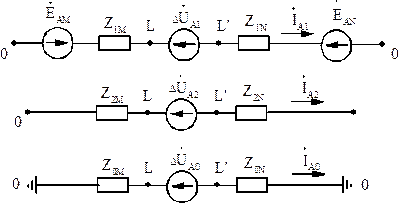
Рис.3.2. Схемы замещения при продольной несимметрии

Этим схемам соответствуют уравнения

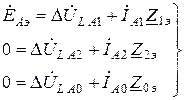, (3.1)

где , , , .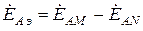

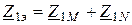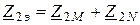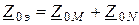Таким образом, напряжения прямой, обратной и нулевой последовательностей в месте продольной несимметрии появляются в результате разложения системы несимметричных векторов фазных напряжений на симметричные составляющие.

Расчёт токов и напряжений в случае продольной несимметрии может быть произведен путём решения системы уравнений (3.1). Система из трёх уравнений содержит 6 неизвестных. Поэтому для её решения используются три дополнительных уравнения исходя из граничных условий, зависящих от вида несимметрии. Далее рассматриваются два вида продольной несимметрии: разрыв одной и двух фаз.

Разрыв одной фазы

Рассмотрим разрыв особой фазы 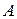(рис.3.3).

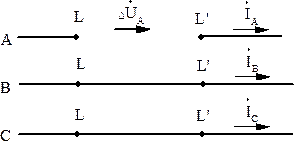
Рис.3.3. Разрыв фазы одной фазы

Этому случаю продольной несимметрии соответствуют граничные условия:

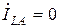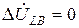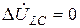, , . (3.2)

Эти условия аналогичны граничным условиям при двухфазном КЗ на землю, что обуславливает и аналогичные расчётные выражения.

Из системы уравнений (2.5) с учётом граничных условий (3.2) получим:

, , .

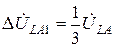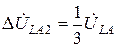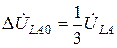Из системы уравнений (3.1)

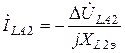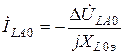, . (3.3)

Так как 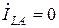, то

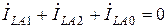. (3.4)

Подставив в (3.4) выражения (3.3), получим

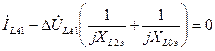
или

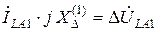, (3.5)

где 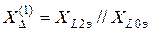(индекс 1 означает разрыв одной фазы).

Из первого уравнения (3.1) с учётом (3.5) получим формулу для вычисления тока прямой последовательности при продольной несимметрии

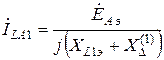. (3.6)

Формула (3.6) аналогична формуле для вычисления тока прямой последовательности при КЗ на основе правила эквивалентности прямой последовательности.

Используя соотношения между симметричными составляющими, получена комплексная схема замещения при разрыве одной фазы (рис. 3.4).

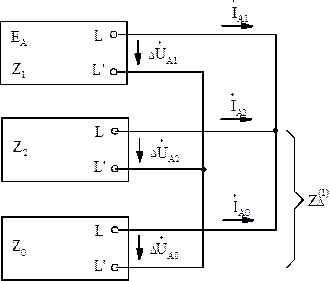
Рис.3.4. Комплексная схема замещения при разрыве одной фазы

Из комплексной схемы замещения находим токи обратной и нулевой последовательностей

,

.

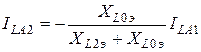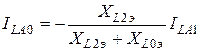Полные токи и напряжения получают путем суммирования векторов прямой обратной и нулевой последовательностей.

Разрыв двух фаз

Рассмотрим разрыв фаз 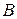и 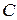(рис.3.5).

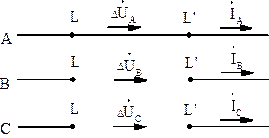
Рис.3.5. Разрыв двух фаз

Этому случаю продольной несимметрии соответствуют граничные условия:

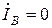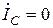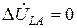, , . (3.7)

При этом граничные условия аналогичны граничным условиям при однофазном КЗ.

Из системы уравнений (2.3) с учётом граничных условий (3.7) получим:

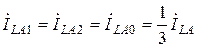, (3.8)

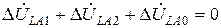. (3.9)

Сложим уравнения системы (3.1) с учётом (3.8) и (3.9) и после несложных преобразований найдем

,

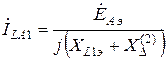где 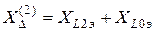(индекс 2 означает разрыв двух фаз).

Для тока в фазе 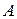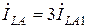. Разность фазных напряжений прямой последовательности в месте разрыва определяется путём сложения двух последних уравнений системы (3.1) с учётом (3.8) и (3.9)

.

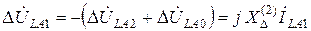Рис.3.6. Комплексная схема замещения при разрыве двух фаз

Используя соотношения между симметричными составляющими (3.8) и (3.9) построена комплексная схема при разрыве двух фаз (рис. 3.6).

Пример 3.1. Для схемы, приведенной на рис.3.7 построить комплексную схему замещения при разрыве одной фазы и двух фаз в начале линии.

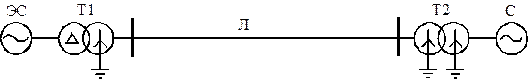
Рис.3.7. Схема участка энергосистемы

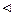Требуемые схемы замещения приведены на рис.3.8 и 3.9 соответственно. Комплексные схемы замещения соответствуют особой фазе А.

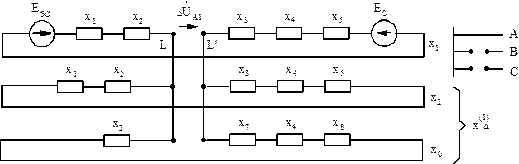
Рис.3.8.Схема замещения при разрыве одной фазы

Рис.3.9.Схема замещения при разрыве двух фаз

Подобные схемы используются, как правило, для расчёта переходных электромеханических процессов, которые протекают сравнительно медленно (1-3 с). Поэтому для генератора задаются переходное сопротивление 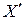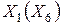(без учёта влияния демпферных контуров) и переходная ЭДС.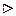

КОНТРОЛЬНЫЕ ВОПРОСЫ К ГЛАВЕ 3

1. Назначение и сущность метода симметричных составляющих.

2. Основные уравнения метода симметричных составляющих.

3. Разрыв одной фазы. Расчёт токов и напряжений.

4. Разрыв двух фаз. Расчёт токов и напряжений.

ЛЕКЦИЯ 15