Приближенный метод исключения элементов
Сущность приближенного метода расчета надежности мостиковых схем методом исключения элементов заключается в том, что в структурной схеме выбираются один или несколько элементов и затем производится расчет показателей надежности для двух крайних случаев:
1) предполагается, что выбранные элементы абсолютно надежны (вероятность безотказной работы элементов равна единице);
2) предполагается, что выбранные элементы абсолютно ненадежны (вероятность безотказной работы элементов равна нулю).
В первом случае две точки системы, к которым подключается элемент, соединяются постоянной связью, во втором – между этими точками отсутствует какая-либо связь. Для двух полученных структур определяются вероятности безотказной работы, соответственно равные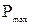 
и 
.
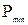Затем определяется средневзвешенное значение вероятностей безотказной работы исключаемых элементов:
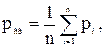(5.42)
где p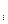 
– вероятность безотказной работы i-го исключаемого элемента; n – число исключаемых элементов.
Окончательно вероятность безотказной работы системы определяется по формуле
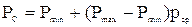. (5.43)
Очевидно, если р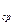 
= 1 (абсолютно надежные исключаемые элементы), то 
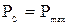. Если 
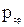= 0 (абсолютно ненадежные элементы), то 
.
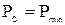Особенности метода исключения элементов:
• с увеличением числа исключаемых элементов точность расчетов понижается;
• с увеличением числа элементов в системе при фиксированном числе исключаемых элементов точность расчетов повышается;
• в качестве исключаемых элементов целесообразно выбирать элементы, имеющие высокую надежность.
Пример 5.7
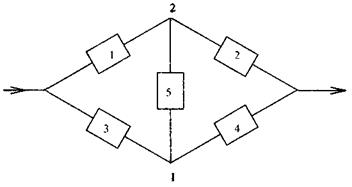Определить приближенно вероятность безотказной работы системы, представленной на рис. 5.18, двумя методами: преобразованием треугольника в звезду и исключением эле-ментов.
Вероятности безотказной работы всех элементов одинаковы:
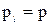= 0,9.
Рис. 5.18
Решение
Преобразуем треугольник, образуемый элементами 1, 3, 5, в звезду с элементами 6, 7, 8 (рис. 5.19). Согласно формулам (5.37) рассчитываем вероятности отказов элементов звезды:
.
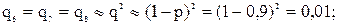
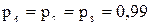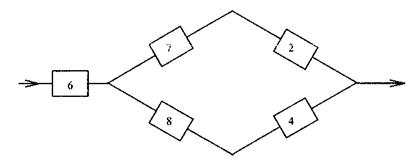
Рис. 5.19
Используя формулы для последовательно и параллельно соединенных элементов, определяем вероятность безотказной работы системы:
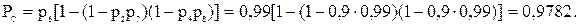
Решим этот же пример методом исключения элементов. В качестве исключаемого выберем элемент 5. Рассмотрим две структуры. В первой из них в месте расположения элемента 5 будет короткое замыкание (рис. 5.20). Поэтому получим
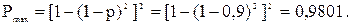
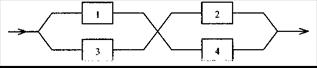
Рис. 5.20
Во второй структуре в месте нахождения элемента 5 будет разрыв цепи
(рис. 5.21).
Поэтому имеем
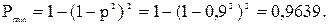
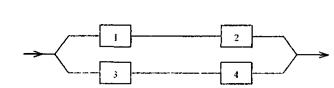
Рис. 5.21
С учетом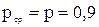 
на основании (5.43) окончательно получаем
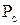= 0,9639+(0,9801-0,9639) 0,9 = 0,9785.
Сравнение значений вероятностей безотказной работы, полученных рассмотренными приближенными методами, показывает, что они очень близки.
6. РАСЧЁТ НАДЁЖНОСТИ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ
ЛОГИКО-ВЕРОЯТНОСТНЫМ МЕТОДОМ
Алгебра логики
Алгебра логики – это раздел математики, занимающийся исчислением высказываний. Под высказыванием Х понимается любое предложение, относительно которого можно утверждать ложно оно или истинно без учёта конкретного содержания. Переменная величина, которая устанавливает лишь два значения 1 и 0, называется двоичной. Функция, определяемая набором двоичных аргументов и принимающая лишь два значения 1 или 0, называется функцией алгебры логики.
В алгебре логики рассматриваются три основные логические операции:
а) НЕ – отрицание. Отрицание высказывания Х обозначается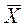 
и значения истинности определяются соотношениями
;
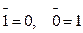б) И-конъюнкция. Конъюнкция (логическое умножение) высказываний Х1 и Х2 истинна тогда и только тогда, когда истинны составляющие её высказываний Х1 и Х2. Значения истинности конъюнкции определяются соотношениями
0 × 0=0, 0 ×1=0 , 1 × 0=0 , 1 × 1 = 1.
в) ИЛИ – дизъюнкция. Дизъюнкция (логическое сложение) высказываний Х1 и Х2 ложна тогда и только тогда, когда ложны составляющие её высказывания Х1 и Х2 . Значения истинности дизъюнкции определяются соотношениями
0+0=0 , 0+1=1 , 1+0=1 , 1+1=1.
Основные правила преобразования:
X × 1=X, X+1=1, X+0=X, X × 0=0,
X × X=X, X+X=X, X ×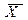 
=0, X+ 
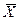=1.
Ассоциативный закон
Х1 × (Х2 × Х3)=(Х1 × Х2) × Х3=Х1 × Х2 × Х3.
Х1+(Х2+Х3)=(Х1+Х2)+Х3=Х1+Х2+Х3.
Коммутативный закон
Х1 × Х2=Х2 × Х1,
Х1+Х2=Х2+Х1.
Дистрибутивный закон
Х1 × (Х2+Х3)=Х1 × Х2+Х1 × Х3,
Х1+(Х2 × Х3)=(Х1+Х2) × (Х1+Х3).
Закон инверсий
,
.
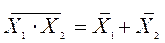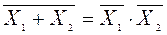Операция поглощения
Х1+Х1 × Х2=Х1 Х1 × (Х1+Х2)=Х1.