Обеспечение надежности на этапе эксплуатации.

Стратегия аварийных замен.

Стратегия связана с простейшей моделью ремонта: после каждого отказа система приводится в исправное состояние за пренебрежимо короткое время и тотчас же возвращается в рабочее состояние. При этом под ремонтом понимается полное восстановление всех исходных свойств системы. Эта модель представляет собой хорошее приближение прежде всего для той практической ситуации, когда имеются резервные системы одного типа. В этом случае теория дает хорошие результаты для планирования потребностей в запасных частях. Исследование рассмотренных вопросов основывается на математической теории восстановления. В дальнейшем, при проведении анализа будем считать, что элемент начинает свою работу в момент t=0 и, проработав случайное время τ₁, выходит из строя. В этот момент он заменяется новым элементом, который, проработав время τ₂, выходит из строя и заменяется третьим элементом. Этот процесс продолжается неограниченно. Естественно предположить, что времена жизни элементов τ₁, τ₂, ... независимы. Случайные времена τ₁, τ₂, ... имеют один и тот же закон распределения, который мы обозначим через F(t):

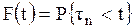
Моменты отказов (рис.5.1) или восстановлений t₁ = τ₁ , t₂ = τ₁ + τ₂ , … , t_n = τ₁ + … + τ_n, образуют случайный поток, который мы будем называть процессом восстановления.

Рис.5.1 Схема процесса восстановления

Фундаментальное значение при изучении процесса восстановления играет так называемая функция восстановлении H(t), которая равна среднему числу отказов, происшедших до момента t.

Можно показать, что функция H(t) удовлетворяет интегральному уравнению

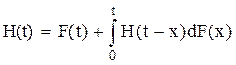(5.1)

Вместо функции H(t) часто рассматривают дифференциальную характеристику

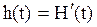
Функция h(t) называется плотностью восстановления.

Плотность восстановления удовлетворяет уравнению восстановления:

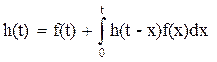(5.2)

Применяя преобразование Лапласа к уравнению восстановления (5.2), получим:

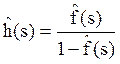(5.3)

Под преобразованием Лапласа функции f(t) принимают функцию

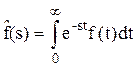
При выводе соотношения (5.3) были использованы известные свойства преобразования Лапласа.

Пусть X₁ и X₂ - взаимно независимые случайные наработки с функциями распределения F₁(t) и F₂(t). Функция распределения суммы X = X₁ + X₂ задается формулой

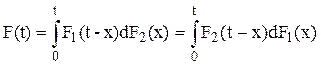
Она называется сверткой функций распределения F₁(t) и F₂(t) и записывается короче в виде

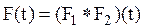
Если плотности f_i(t) = F'_i(t), i = l, 2, существуют, то сумма X так же имеет плотность, которая задается формулой

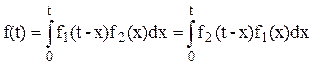
Плотность распределения такого вида называют сверткой плотностей распределения f₁(t) и f₂ (t). В этом смысле определено и понятие свертки двух функций f₁ и f₂, заданных на интервале [0, ∞), даже когда они не являются плотностями распределения.

По аналогии .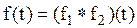

Применение преобразования Лапласа к свертке 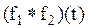дает

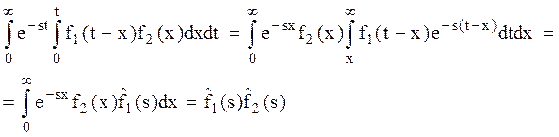
Таким образом, преобразование Лапласа свертки равно произведению преобразований Лапласа:

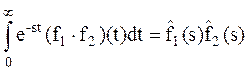
Пусть функции f₁(t) и f₂(t) обладают указанными выше свойствами. Тогда

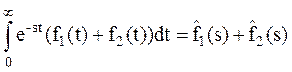
Следовательно, преобразование Лапласа суммы равно сумме преобразований Лапласа.

При некоторых видах закона распределения F(t) можно получить удобные формулы для введенных выше показателей надежности восстанавливаемого элемента, если восстановление происходит мгновенно.

Для случая экспоненциального закона распределения времени между восстановлениями или отказами процесс восстановления является пуассоновским потоком и вероятность получения ровно m восстановлений (отказов)

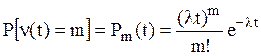, (5.4)

где λt - математическое ожидание числа восстановлений (отказов) на интервале (0, t).

Действительно, математическое ожидание числа восстановлений на интервале (0, t) по определению принимает вид

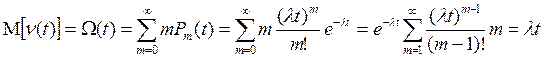
Отсюда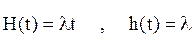

Таким образом, для экспоненциального закона плотность восстановления, или параметр потока отказов h(t), т. е. среднее числа отказов восстанавливаемого элемента в единицу времени, численно равно интенсивности отказов λ невосстанавливаемого, работающего до первого отказа элемента, хотя величина λ является условной плотностью вероятности того, что невосстанавливаемый элемёнт, проработавший до времени t безотказно, откажет на интервале (t, t + Δt), а h(t) - безусловная плотность вероятности отказа (восстановления) восстанавливаёмого элемента в момент t.

Если интервалы τ₁, τ₂, ..., τ_i, … между соседними восстановлениями (отказами) распределены нормально, то случайная величина t_m = t = τ₁ + τ₂ + ... + τ_i + … + τ_m как линейная функция от независимых нормально распределенных величин имеет также нормальный закон с математическим ожиданием

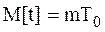, (5.5)

где T₀ - среднее время безотказной работы элемента.

Дисперсия случайной величины t = t_m может быть найдена в виде

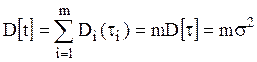, (5.6)

где 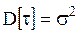- дисперсия времени между соседними отказами.

В соответствии с (5.5) и (5.6) закон распределения случайной величины t принимает вид

,

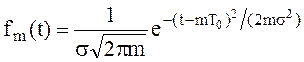а математическое ожидание числа отказов или восстановлений за время t определяется выражением

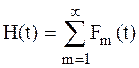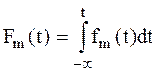, где (5.7)

Для большинства других законов распределения функция F_m(t) не выражается в конечном виде. Поэтому полезно знать упрощенные оценки для функции восстановления H(t):

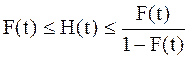
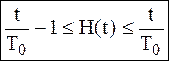
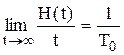(5.8)

Для среднего времени 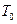существует интервальная оценка .В частности для горячего резерва (см. рис. 5.2) среднее время можно оценить по интервальному соотношению :

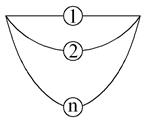
Рис 5.2 Схема резервированной системы.

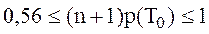
Отсюда 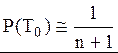где n - общее число элементов,

Для закона Вейбулла ( 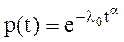) имеем:

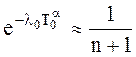
Отсюда

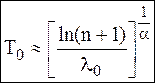
Полученные результаты позволяют оценивать необходимое количество запасных частей. Очевидно среднее количество запасных частей не обеспечивает гарантированного результата, так как реально число отказов 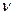может больше, чем их среднее число . Гарантированное число резервных элементов можно оценить из условия

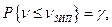(5.9)

где 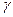- заданный уровень доверия; 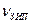- число запасных элементов.

Для экспоненциального закона распределения наработки на отказ соотношение примет вид

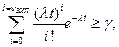
где 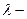интенсивность отказа; 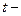заданное время работы устройства.

При длительном функционировании можно найти ассинптотическую оценку числа отказов. В этом случае случайное число отказов имеет нормальное распределение с параметрами

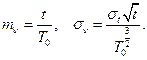
Очевидно гарантированное количество запасных частей может быть найдено из условия

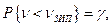
где 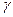- принятый уровень доверия.

Раскрывая выражение для вероятности, получим

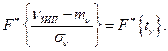
Отсюда

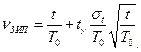
Лекция №15