Статистический приемочный контроль продукции .
( метод Неймана- Пирсона )
Задача проверки гипотезы заключается в определении критической области 
максимальной мощности при заданной вероятности ошибки первого рода 
. Очевидно, при этом мы будем иметь минимальную вероятность ошибки второго рода 
.
При проверке простой гипотезы 
против простой альтернативы 
эта задача сводится к выбору критической области . Для определения критической области статистики используют уровень значимости и учитывают вид альтернативной гипотезы . Основная гипотеза о значении неизвестного параметра 
распределения выглядит так:
.
Альтернативная гипотеза имеет при этом следующий вид:
Соответственно можно получить левостороннюю, правостороннюю или двустороннюю критические области.
Проверка статистической гипотезы состоит из следующих этапов:
1) определение гипотез и ;
2) выбор статистики и задание уровня значимости ;
3) определение по таблицам, по уровню значимости и по альтернативной гипотезе критической области;
4) вычисление по выборке значения статистики;
5) сравнение значений статистики с критической областью;
6) принятие решения: если значение статистики 
не входит в критическую область, то принимается гипотеза и отвергается гипотеза , а если входит в критическую область, то отвергается гипотеза и принимается гипотеза .
7) приемочный уровень 
и число испытаний 
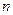определяются из решения системы:
.
В дальнейшем предположим, что случайная величина Х распределена нормально.
Ставится задача различения двух гипотез о значении математического ожидания:
Для заданного риска поставщика , имеем
;
где -- приемочный уровень, 
-- точечная оценка математического ожидания.
Отсюда
;
где 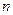-- объем выборки, 
-- среднее квадратическое отклонение.
Приравнивая аргументы, получим
.
Принимая риск заказчика ,равным ,найдем
;
Отсюда
;
Приравнивая аргументы, получим
.
Вычитая из первого равенства второе, найдем
;
Отсюда 
(4.1)
Из первого соотношения имеем
Отсюда
(4.2)
Задача выборочного контроля в данном случае состоит в том, чтобы по результатам анализа выборочных характеристик (среднего арифметического значения 
) сделать заключение о браковке или приемки партии.
В дальнейшем рассмотрим схему проведения количественного контроля. Предположим, что партия забраковывается, когда процент брака равен 
и принимается когда процент брака равен 
.
Таким образом требуется различить две гипотезы:
гипотеза 
приемка партии;
гипотеза 
браковка партии.
От исходных гипотез перейдем к гипотезам различения математических ожиданий:
; 
.
При решении задачи предположим, что отказ наступает при выполнении условия 
.
Тогда, в предположении нормального закона распределения, вероятность отказа будет равна
,
где 
аргумент функции нормированного нормального распределения, соответствующий вероятности отказа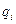 
. Приравнивая аргументы, получим
Отсюда найдем 
.
Для определения приемочного уровня 
и числа испытаний n воспользуемся соотношениями (4.1) и (4.2) . Учитывая, что 
, получим
,
где 
; 
.
Пример. Рассмотрим задачу различения двух гипотез :
приемка партии,
браковка партии.
При задании исходных данных воспользуемся результатами статистической обработки механических свойств листов из сплава АМг6Н :
МПа – математическое ожидание предела прочности,
МПа - среднее квадратическое отклонение предела прочности,
МПа - предел прочности материала по ГОСТу,
- риски поставщика и заказчика.
Результаты расчетов представлены ниже:
Заметим, что для партии листов с принятыми характеристиками, вероятность брака будет равна
Лекция №13