Расчет надежности систем произвольной структуры.

При оценке надежности систем произвольной структуры, на основе анализа функционирования систем, определяются возможные состояния системы и переходы между ними. По результатам этого анализа строится граф состояний системы. Предположим, что граф состояний имеет вид, представленный на рис. 2.6.

Рис. 2. 6 Граф состояний системы.

Каждое состояние системы на графе представлено прямоугольниками. Стрелками отмечены возможные переходы из одного состояния в другое. Каждой стрелке соответствует определенная интенсивность отказа. Допустим, далее, что из анализа функционирования системы определены работоспособные состояния системы, то есть состояния, при нахождении в которых система будет выполнять поставленную перед ней задачу. Тогда надежность будет определяться вероятностью нахождения системы в одном из работоспособных состояний. Если предположить, что для рассматриваемого примера работоспособными являются состояния 1 и 2, то надежность такой системы запишется в виде

Н = Р₁ + Р₂ ,

где Р₁ , Р₂ – соответственно вероятности нахождения системы в первом и втором состояниях. Искомые вероятности находятся в результате решения системы дифференциальных уравнений Колмогорова. Число уравнений равно числу всех состояний. Уравнения для каждого состояния составляются по следующему правилу:

слева записывается производная по времени от вероятности нахождения системы в данном состоянии, справа записывается сумма членов, число членов равно числу стрелок, выходящих или входящих в рассматриваемое состояние, каждый член равен произведению интенсивности отказа, стоящей при стрелке, умноженной на вероятность того состояния, из которого исходит стрелка. Знак при слагаемом берется со знаком «+», если стрелка «втекает» в рассматриваемое состояние и со знаком «- », если стрелка «вытекает» из него.

Для графа, представленного на рис.2.6., система дифференциальных уравнений примет вид

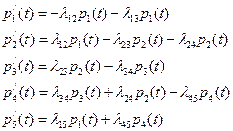(2.12)

Для получения единственного решения необходимо задать пять начальных условий:

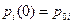, i=1,2,….5.

Так как в каждый момент времени система обязательно находится в одном из рассматриваемых состояний, любое уравнение системы может быть заменено условием нормировки

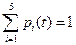. (2.13)

Системы дифференциальных уравнений рассмотренного типа могут быть решены операторным методом. Для этого к обоим частям уравнения применяют преобразование Лапласа ( см. табл.2.3 )

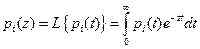
Согласно свойству преобразования Лапласа имеем

.

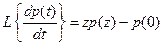Применяя преобразование Лапласа к системе (2.12), приходим к системе алгебраических уравнений относительно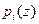

Преобразования Лапласа Таблица 2.3

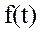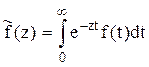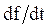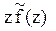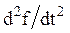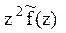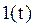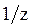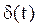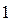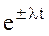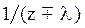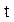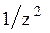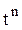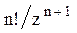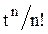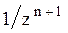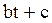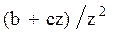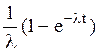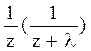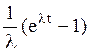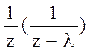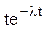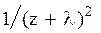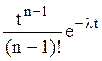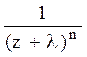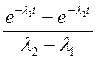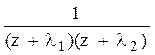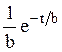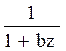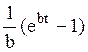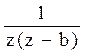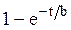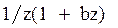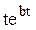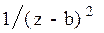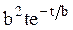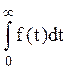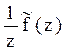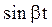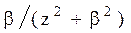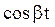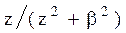Лекция №5

Оценка средней наработки до отказа

Для нахождения среднего времени 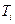пребывания системы в i –ом состоянии воспользуемся преобразованием Лапласа для вероятности нахождения системы в этом состоянии

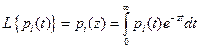
Переходя к пределу при 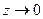, получим

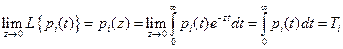
Соответственно для производных получим

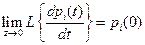, где 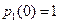, 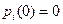( i=2,3,…n)

Учитывая полученные соотношения и применяя предельный переход к обоим частям

алгебраических уравнений (2.12),получим систему уравнений относительно .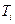

Знание 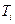позволяет определить среднее время работы системы до достижения любого j-го состояния .

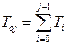Для иллюстрации этого метода определим среднее время до отказа резервированной системы .При проведении расчета примем кратность «горячего» резерва равна трем. Интенсивность отказа элементов равна 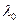. Элементы системы не восстанавливаются.

Для графа системы, представленного на рис. 2.7, система алгебраических уравнений примет вид

.

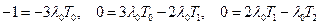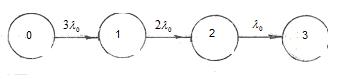
Рис. 2.7 Граф состояний системы.

После преобразований получим

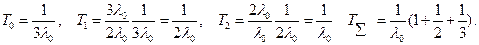
« Холодное» резервирование.

В случае «холодного» резервирования работает только основной элемент, а запасные элементы бездействуют. Граф состояний такой системы для n-1-го резервного элемента представлен на рис.2.8

Рис. 2.8 Граф состояний системы.

Первое состояние графа соответствует случаю безотказного функционирования основного элемента, второе состояние соответствует отказу основного элемента и безотказному функционированию первого запасного элемента и т д. Наконец, последнее состояние соответсвует отказу всей системы. Очевидно надежность такой сиситемы будет определяться вероятностью нахождения системы в первых n состояниях, то-есть

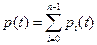
где 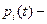вероятность нахождения системы в i-том состоянии.

Для оценки составляющих 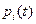запишем систему дифференциальных уравнений Колмогорова для графа, представленного на рис. 2

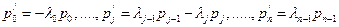
Система решается при начальных условиях .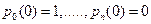

Решая систему операторным методом, получим

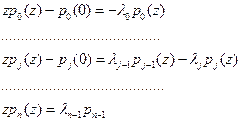
Таким образом

.

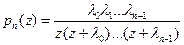Если 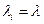, получим

.

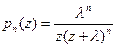Соответственно для оригинала имеем

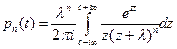
После преобразований найдем

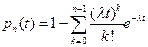
Полученный результат можно представить в виде

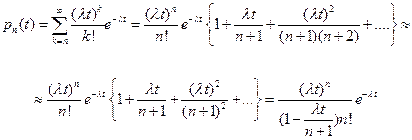
Если предположить, что 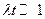, получим приближенную оценку вероятности отказа системы

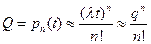, где q – вероятность отказа системы.

Очевидно, величина 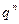характеризует вероятность отказа в случае «горячего» резерва.

Таким образом при идеальном переключателе ненагруженный резерв лучше нагруженного.

Однако при неидеальном переключателе необходимо учитывать вероятность его отказа, что ухудшает характеристики надежности для ненагруженного резерва.

Понятие о коэффициенте готовности.

Если число состояний анализируемой системы S конечно и из каждого состояния можно перейти в любое другое, то существуют предельные вероятности состояний, не зависящие от начального состояния системы. Например, система, представленная графом состояний на рис.2.9 , удовлетворяет этим требованиям и, следовательно, приходит со временем к стационарному режиму.

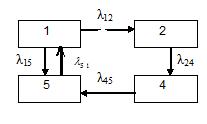
Рис.2.9 Граф состояний системы.

Предельные вероятности состояний дают средние относительные величины времени пребывания системы в данном состоянии. Для вычисления предельных вероятностей состояний нужно составить систему уравнений Колмогорова и положить ее левые части равными нулю. В этом случае система дифференциальных уравнений превратится в систему линейных алгебраических уравнений..

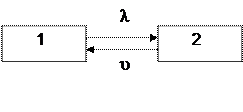
Рис. 2.10 Граф состояний системы.

Для иллюстрации рассмотренного метода найдем выражение для расчета надежности восстанавливаемого элемента системы. При анализе восстанавливаемых систем вводится понятие интенсивности восстановления ν. Согласно определению под интенсивностью восстановления ν(t) понимается условная плотность распределения времени восстановления, найденная при условии, что до момента t элемент не восстановлен. Граф состояний восстанавливаемого элемента представлен на рис. 2.10. Здесь первое состояние соответствует работоспособному состоянию элемента, а второе – состоянию отказа. Система дифференциальных уравнений для рассматриваемого случая запишется так:

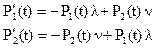(2.14)

Для простоты будем считать, что интенсивности отказа и восстановления не меняются по времени. Кроме того, предположим, что в начальный момент система находится в исправном состоянии. Таким образом, начальные условия запишутся в виде

Р₁(0) = 1; Р₂ = 0 (2.15)

Складывая первое и второе уравнения, получим

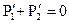
Отсюда

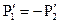Дифференцируя первое уравнение, приходим к уравнению 2-го порядка

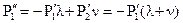(2.16)

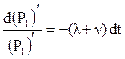Уравнение (2.16) можно рассматривать как уравнение с разделяющимися переменными относительно Р´₁, т.е.

(2.17)

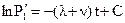Отсюда

Экспоненциируя, получим

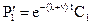(2.18)

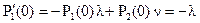Для нахождения С₁ определим начальные условия для Р´₁(0). Учитывая (2.14) и (2.15), получим

(2.19)

Подставляя начальное значение в (2.18), найдем

С₁ = - λ (2.20)

Интегрируя (2.18), будем иметь

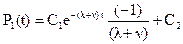(2.21)

Подставляя в (2.21) начальные условия , определим С₂

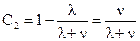(2.22)

Таким образом, окончательно будем иметь

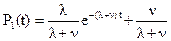(2.23)

Заметим, что при 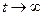мы приходим к стационарному решению 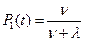(2.24)

Выражение (2.24) определяет вероятность того, что в произвольный момент времени элемент находится в работоспособном состоянии. Стационарное значение 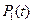обычно принимается за коэффициент готовности элемента. Физически коэффициент готовности характеризует среднюю долю времени нахождения элемента в работоспособном состоянии. Заметим, что стационарное решение может быть получено более просто, как решение системы алгебраических уравнений, полученных из (1) приравниванием 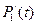к нулю

Схема гибели и размножения.

Согласно полученным выше результатам ,имея в расположении размеченный граф состояний, можно легко напасать уравнения Колмогорова для вероятностей состояний, а также написать и решить алгебраические уравнения для финальных вероятностей. Для некоторых случаев удается последние уравнения решить заранее, в буквенном виде. В частности, это удается сделать, если граф состояний системы пред­ставляет собой так называемую «схему гибели и раз­множения» Граф состояний для схемы гибели и размножения имеет вид, показанный на рис.2.11 .

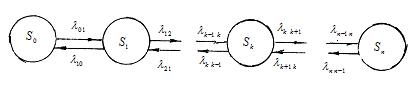
Рис. 2.11 Граф схемы « гибели и размножения ».

Особенность этого графа в том, что все состояния системы можно вытя­нуть в одну цепочку, в которой каждое из средних со­стояний (S₁, S₂, … S_n-1) связано, прямой и обратной стрелкой с каждым из соседних состоянии — правым и левым, а крайние состояния. (S₀, S_n)—только с од­ним соседним состоянием. Термин «схема гибели и раз­множения» ведет, начало от биологических задач, где подобной схемой описывается изменение численности популяции.

Схема гибели и размножения очень часто встреча­ется в разных задачах практики,, поэтому полезно, одни раз и навсегда, найти для нее финальные вероятности состояний.

Предположим, что все потоки событий, переводя­щие систему по стрелкам графа,— простейшие (для краткости будем называть и систему S и протекаю­щий в ней процесс — простейшими).

Пользуясь графом рис.2.11 составим и решим алгебраические уравнения для финальных вероятно­стей состояний (их. существование вытекает из того, что из каждого состояния можно перейти в каждое другое) Для стояния S₀ имеем:

.

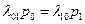Для второго состояния S₁ : .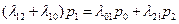

Равенство приводится к виду .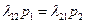

Далее, совершенно аналогично .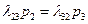

и вообще 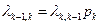, где к принимает все значения от 0 до n..

Итак, финальные вероятности р₀, р₁,…, р_nудовлетворяют уравнениям

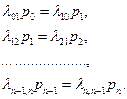
Кроме того, надо учесть нормировочное условие

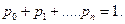
Решим эту систему уравнений из первого уравнения выразим р₁через р₀:

.

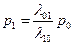Из второго, получим: ,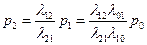

из третьего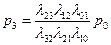

и вообще, для любого k (от 1 до n) .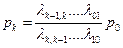

Обратим внимание на то, что в выражении для 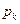в числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данногo состояния S_k), а в знаменателе — произведение всех интенсивностей стоящих у стрелок, ведущих справа налево (с начала и до S_k )

Таким образом, все вероятности состояний р_0,... р_п выражены черед одну из них (р₀). Подставим эти выражения в нормировочное условие, вынося за скобку р₀

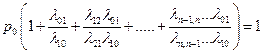
Отсюда получим выражение для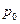

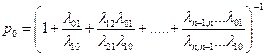
. Все остальные вероятности выражены через р₀ . Заметим, что коэффициенты при р₀ в каждой из них представляют собой не что иное, как последовательные члены ряда, стоящего после единицы в формуле для 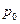. Значит, вычисляя р₀, мы уже нашли все эти коэффициенты Полученные формулы очень полезны при решении простейших задач теории надежности и массового обслуживания.

Лекция №6