Расчет надежности резервированных систем.

Системы с параллельным соединением элементов

В дальнейшем рассмотрим методы расчета надежности систем с параллельным соединением элементов. Для упрощения выкладок проведем анализ работоспособности простейшей системы из двух элементов. Согласно данному выше определению, отказ такой системы происходит, когда отказывают оба элемента (и первый и второй). Таким образом, вероятность отказа Q определяется вероятностью совместного выполнения неравенств

ρ₁ < 0 и ρ₂ < 0 ,

то есть Q = P{ρ₁ < 0; ρ₂ < 0 } (2.8)

Применяя к (2.8) теорему умножения вероятности, получим

Q = P{ρ₂ < 0}P{ρ₁ < 0 / ρ₂ < 0}

Очевидно, для независимых элементов соотношение примет вид

Q = P{ρ₁ < 0}P{ρ₂ < 0} = (1 – h₁)(1 – h₂)

где h₁ = P{ρ₁ > 0}, h₂ = P{ρ₂ > 0}

Отсюда надежность системы будет равна

H = 1 – Q = 1 - (1 – h₁)(1 – h₂) (2.9)

Если элементы зависимы, для оценки надежности необходимо вычислять условные вероятности P{ρ₁ < 0 / ρ₂ < 0}. Рассмотрим определение этой вероятности для случая линейно зависимых элементов.

Как видно из графика при ρ₂ < 0 значения всегда отрицательны. Следовательно, условная вероятность P{ρ₁ < 0 / ρ₂ < 0} будет равна единице как вероятность достоверного события. Отсюда

Q = P{ρ₂ < 0} = 1 – h₂

Как было показано выше, второй элемент имеет максимальную надежность. Поэтому соотношение можно записать так

Q = 1- max { h₁ , h₂}

Отсюда

Н = 1 – Q = max { h₁ , h₂}

Полученные выше результаты позволяют записать следующую интервальную оценку

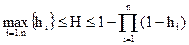(2.9)

Равенство справа выполняется в случае независимости элементов (r = 0). Нижняя оценка является точной для системы с линейно зависимыми элементами (r = 1). При промежуточных значениях коэффициента корреляции надежность лежит внутри диапазона (2.9). Равенство справа используется для оценки надежности систем с «горячим» резервированием.

«Горячее» резервирование – резервирование с постоянным включением резервных элементов (см. рис.2.2 ).Такое резервирование возможно, когда подключение резервного элемента не существенно изменяет рабочий режим устройства. Достоинством такого резервирования является постоянная готовность резервного элемента. Безотказность схемы в этом случае определяется по формуле

H = 1 – (1 – h)ⁿ (2.10)

где h – надежность одного устройства, n – число резервных элементов с учетом основного.

В реальной практике помимо « горячего» резервирования используется «холодное» резервирование. «Холодное» резервирование --- резервирование раздельное с замещением отказавшего элемента резервным. При этом рабочий режим основного устройства не искажается. Однако при таком резервировании необходимо затрачивать определенное время на подключение резервного элемента и учитывать вероятность отказа переключателя.

Общее резервирование.

В заключении остановимся на оценке надежности при таком резервировании, когда для обеспечения успешного функционирования системы необходимо, чтобы определенное число устройств сохраняло свою работоспособность. Например, для выполнения программы достаточно иметь ДУ, состоящую из l одинаковых двигателей. Для повышения надежности в ДУ включают дополнительно m резервных двигателей.

Для упрощения выкладок анализ общего резервирования проведем для двигательной установки, состоящей из четырех изолированных двигателей, допускающей возможность отказа любых двух из них. Согласно условию ДУ будет выполнять поставленную задачу при следующих ситуациях:

- ни один из двигателей не отказал (событие А₀);

- отказал один из двигателей (событие А₁);

- отказали два двигателя (событие А₂).

Тогда вероятность безотказной работы ДУ можно представить в виде

Н = Р{ А₀ U А₁ U А₂} (2.11)

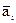В дальнейшем обозначим безотказное функционирование i-го двигателя, как выполнение события а_i. Тогда отказ этого двигателя определяется противоположным событием . С учетом введенных обозначений событие А_i можно записать так

А₀ = {a₁∩a₂∩a₃∩a₄}

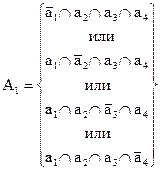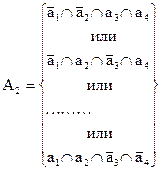Как видно из этих соотношений все события в круглых скобках попарно несовместимы, так как каждое из них включает противоположное событие. Следовательно, и события будут несовместны. Поэтому соотношение (2.11) можно представить в виде

Н = Р(А₀) + Р(А₁) + Р(А₂)

Считая отказы отдельных двигателей независимыми событиями для вероятностей Р(А_i), получим

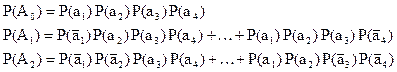Для равнонадежных двигателей эти соотношения запишутся так

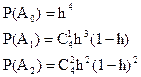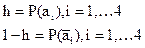где

После подстановки окончательно получим

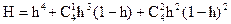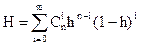Полученные результаты могут быть обобщены на общий случай. Пусть ДУ состоит из n одинаковых двигателей. Причем, для выполнения задачи достаточно иметь в исправном состоянии l блоков, а m = n – l находятся в «горячем» резерве. Тогда соотношение примет вид

Рассмотренный выше тип резервирования используется для повышения надежности двигательных установок. В частности, в ДУ первой ступени РН «Сатурн 1» допускался выход из строя одного из 8 ЖРД Н-1. При этом расчетное соотношение примет вид

Н_ДУ = h⁸ + 8h⁷(1 – h)

где h = 0,965 – надежность одного двигателя.

После подстановки получим

Н_ДУ = 0,75 + 0,21 = 0,96

В случае отсутствия резервного двигателя оценка надежности ДУ равна

Н_ДУ,0 = h⁷ = 0,965⁷ = 0,78

Таким образом введение резервного двигателя позволяет существенно поднять уровень надежности ДУ.

Рассмотренный выше подход может быть использован так же для оценки надежности при мажоритарном резервировании, применяемом для повышения точности работы СУ.

В случае, когда в системе из 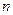элементов 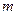из них находятся в «холодном» резерве, приходим к «скользящему» резервированию. В этом случае выражение для оценки надежности примет вид

;

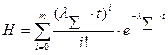где 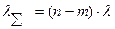, 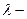интенсивность отказа одного элемента.