Параллельное соединение звеньев
При параллельном соединении на вход всех звеньев подается общий сигнал, а на выходе образуется сигнал, являющийся суммой выходных сигналов звеньев. Результирующая передаточная функция равна сумме передаточных функций отдельных звеньев:
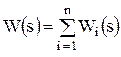. (4.2)
В пакете Simulink параллельное соединение получаем с помощью сумматора (Sum), который находится в разделе Math основной библиотеки Simulink (рис.4.2).
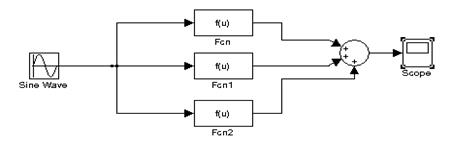
Рис.4.2. Параллельное соединение звеньев в пакете Simulink
Звено, охваченное обратной связью
При соединении обратной связью выходной сигнал первого звена является входным для второго. Причем входной сигнал первого звена образуется в результате сложения или вычитания входного сигнала первого звена и выходного сигнала второго звена. Результирующая передаточная функция будет описываться выражением
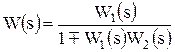. (4.3)
Знак (−) в этой формуле ставится при положительной обратной связи, т.е. при сложении сигналов, а знак (+) при отрицательной обратной связи, т.е. при вычитании сигналов. Если второе звено отсутствует в цепи обратной связи, то передаточная функция примет вид
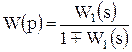. (4.4)
В пакете Simulink соединение с обратной связью получаем с помощью сумматора, указывая знак обратной связи (рис.4.3). Для этого необходимо два раза нажать левой кнопкой мыши на его изображении, в появившемся окне приводятся знаки входов сумматора слева направо по часовой стрелке, которые по умолчанию оба положительны (++). Чтобы сделать второй вход отрицательным, необходимо изменить второй знак на отрицательный.
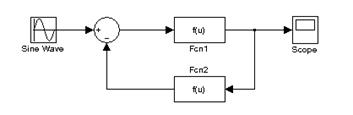
Рис.4.3. Звено, охваченное обратной связью,
в пакете Simulink
В случае охвата обратной связью группы звеньев, что характерно для управления по отклонению, передаточная функция замкнутой системы будет иметь вид
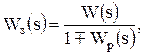(4.5)
где W(s) – передаточная функция цепочки звеньев от входного до выходного воздействия; Wр(s) – передаточная функция разомкнутой системы, то есть цепочки из всех звеньев системы, получающейся после разрыва обратной связи.
Для системы, изображенной на рис. 4.3, W(s) = W1(s), а Wp(s) = W1(s)×W2(s) и передаточная функция замкнутой системы превращается в уравнение (4.3).
5. РЕШЕНИЕ ЗАДАЧ АНАЛИЗА ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Задача анализа линейных систем автоматического управления включает в себя определение свойств системы в целом (показателей устойчивости и качества) при известных характеристиках входящих в нее звеньев.
Таким образом, для проведения анализа системы автоматического управления необходимо и достаточно определить устойчивость, запасы устойчивости и показатели качества системы автоматического управления и сравнить их с предельными показателями устойчивости и качества, заданными для данной системы.
Понятие устойчивости и критерии устойчивости систем
Автоматического управления
Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
Это понятие хорошо описывается тремя простыми примерами (рис.5.1):
1. Шар, находящийся на вершине горки (рис.5.1, а), является примером неустойчивой системы, так как при приложении к нему конечного возмущения (сторонней силы) он скатится с горки и в исходное положение не вернется.
2. Шар, находящийся во впадине, является примером устойчивой системы, так как при приложении к нему конечного возмущения он вернется в исходное положение (рис.5.1, б).
3. Шар, находящийся на плоскости, является примером системы, находящейся на границе устойчивости, так как при приложении к нему конечного возмущения он остановится, но уже в другом положении (рис.5.1, в).
 |
Рис.5.1. Пример, иллюстрирующий понятие устойчивости
Таким образом, если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. А если система устойчива, то переходный процесс в системе, вызванный каким-либо воздействием, со временем затухает, и система вновь возвращается в устойчивое состояние.
Вышеприведенное понятие устойчивости определяет устойчивость установившегося режима системы, тогда как система может работать в условиях непрерывно изменяющихся воздействий, когда установившийся режим вообще отсутствует. Тогда с учетом таких условий работы можно дать следующее, более общее определение устойчивости: система устойчива, если ее выходная величина остается ограниченной в условиях действия на систему ограниченных по величине возмущений.
Устойчивость является основной оценкой динамических свойств систем автоматического управления. Устойчивость систем автоматического управления связана с характером её поведения после прекращения внешнего воздействия. Это поведение описывается свободной составляющей решения дифференциального уравнения, которое описывает систему. Если свободная составляющая рабочего параметра объекта управления после прекращения внешнего воздействия стремится к нулю, то такая система является устойчивой. Другими словами, устойчивость системы − это есть затухание ее переходных процессов.
Если свободная составляющая стремится к конечному значению или имеет вид гармонических колебаний с постоянной амплитудой, то система считается нейтральной. В том случае, если свободная составляющая неограниченно возрастает или имеет вид гармонических колебаний с возрастающей амплитудой, то система считается неустойчивой.
Оценка устойчивости производится на основе результатов исследования свободной составляющей, которая представляет собой решение однородного дифференциального уравнения (которое называется характеристическим) при заданных начальных условиях:
(a0sn+a1sn-1+...+an-1)y=0. (5.1)
При этом система автоматического управления будет устойчива, если переходный процесс, вызванный любым возмущением, будет затухающим, то есть с течением времени будет стремиться к какому-то определенному значению. Для выполнения этого условия необходимо, чтобы действительная часть сопряженных корней характеристического уравнения системы была отрицательной.
В общем случае это требует составления передаточной функции замкнутой системы и получения корней характеристического уравнения, что достаточно сложно и трудоемко для сложных систем выше 3-го порядка.
Поэтому с целью упрощения анализа устойчивости систем разработан ряд специальных методов, которые получили название критериев устойчивости.
Критерии устойчивости делятся на две разновидности: алгебраические и частотные. Алгебраические критерии являются аналитическими, а частотные – графоаналитическими. Критерии устойчивости позволяют также оценить влияние параметров системы на устойчивость в виде запасов устойчивости.
В пакете Simulink возможно автоматическое применение трех критериев устойчивости:
1) по корням характеристического уравнения системы;
2) частотные критерии устойчивости Найквиста;
3) критерий устойчивости Никольса.
В нашей стране применяются в основном первые два.
5.1.1. Критерий устойчивости по корням