Связи, накладываемые на систему. Степень статической неопределимости.

Для решения большинства статически неопределимых встречающихся на практике задач обозначенные приемы оказываются, однако, далеко не достаточными. Поэтому необходимо остановиться на более общих методах раскрытия статической неопределимости на примере стержневых систем.

Под стержневой системой в широком смысле слова понимается всякая конструкция, состоящая из элементов, имеющих форму бруса. Если элементы конструкции работают в основном на растяжение или сжатие, то стержневая система называется фермой (рис. 1).

Рис.1. Расчетная схема формы

Ферма состоит из прямых стержней, образующих треугольники. Для формы характерно приложение внешних сил в узлах.

Если элементы стержневой системы работают в основном на изгиб или кручение, то система называется рамой (рис. 2).

Особую, наиболее простую для исследования группу стержневых систем составляют плоские системы. У плоской рамы или фермы оси всех составляющих элементов до и после деформации расположены в одной плоскости. В этой же плоскости действуют все внешние силы, включая и реакции опор (см. рис. 2,а).

Наряду с плоскими рассматриваются так называемые плоско-пространственные системы. Для такого рода систем оси составляющих элементов в недеформированном состоянии располагаются, как и для плоских систем, в одной плоскости. Внешние же силовые факторы действуют в плоскостях, перпендикулярных к этой плоскости (рис. 2,в). Стержневые системы, не относящиеся к двум указанным классам, называются пространственными (рис.2,в).

Рамы и фермы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая кинематически неизменяемая система, для которой все реакции опор могут быть определены при помощи уравнений равновесия, а затем при найденных опорных реакциях методом сечений могут быть найдены также и внутренние силовые факторы в любом поперечном сечении. Под статически неопределимой системой имеется в виду такая, опять же кинематически неизменяемая система, для которой определение внешних реакций и внутренних силовых факторов не может быть произведено при помощи метода сечений и уравнений равновесия.

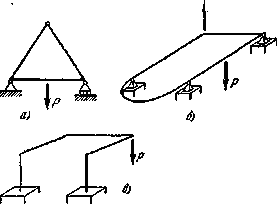
а) плоская, б) плоскопространственная. в) пространственная

Рис.2. Расчетные схемы рамных конструкций:

Разность между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы, носит название степени или числа статической неопределимости. В зависимости от этого числа системы разделяются на один, два, три...., n раз статически неопределимые. Иногда говорят, что степень статической неопределимости равна числу дополнительных связей, наложенных на систему. Остановимся на этом вопросе подробнее.

Положение жесткого бруса в пространстве определяется шестью независимыми координатами, иначе говоря, жесткий брус обладает шестью степенями свободы. На брус могут быть наложены связи, т. е. ограничения, обусловливающие его определенное положение в пространстве. Наиболее простыми связями являются такие, при которых полностью исключается то или иное обобщенное перемещение для некоторых сечений бруса. Наложение одной связи снимает одну степень свободы с бруса как с жесткого целого. Следовательно, если на свободный жесткий брус наложено шесть связей, то положение его в пространстве как жесткого целого будет, за некоторыми исключениями, определено полностью и система из механизма, обладающего шестью степенями свободы, превращается в кинематически неизменяемую систему. То число связей, при котором достигается кинематическая неизменяемость, носит название необходимого числа связей. Всякую связь, наложенную сверх необходимых, называют дополнительной. Число дополнительных связей равно степени статической неопределимости системы.

Связи в рамах и стержневых системах делят обычно на связи внешние и связи внутренние, или взаимные. Под внешними связями понимаются условия, накладываемые на абсолютные перемещения некоторых точек системы.

а)внешняя связь, б) две внешние связи в) шесть внешних связей в общем случае

Рис.3. Схемы эквивалентных связей

Если, например, на левый конец бруса (рис. 3, а) наложено условие, запрещающее вертикальное перемещение, говорят, что в этой точке имеется одна внешняя связь. Условно она изображается в виде двух шарниров или катка. Если запрещено как вертикальное, так и горизонтальное смещение, говорят, что наложены две внешние связи (рис. 3, б). Заделка в плоской системе дает три внешние связи. Пространственная заделка соответствует шести внешним связям (рис. 3, б). Внешние связи часто, как уже упоминалось, делят на необходимые и дополнительные. Например, на рис. 4, а и б показана плоская рама, имеющая в первом случае три внешние связи, а во втором — пять внешних связей. Для того чтобы определить положение рамы в плоскости как жесткого целого, необходимо наложение трех связей. Следовательно, в первом случае рама имеет необходимые внешние связи, а во втором, кроме того, две дополнительные внешние связи.

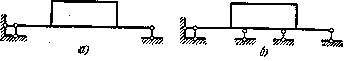
а) три внешних связи, б) пять внешних связей

Рис.4. Плоская рама

Под внутренними, или взаимными, связями понимаются ограничения, накладываемые на взаимные смещения элементов рамы. Здесь также можно говорить как о необходимых, так и о дополнительных связях. Так, например, плоская рама, показанная на рис. 5, а, имеет необходимое количество как внешних, так и внутренних связей между элементами. Это — кинематически неизменяемая система. Если будут заданы внешние силы, мы сможем найти как реакции опор, так и внутренние силовые факторы в любом поперечном сечении рамы. В той же раме, показанной на рис. 5, б, дополнительно наложены две дополнительные внутренние связи, запрещающие взаимное вертикальное и горизонтальное смещения точек А и В. Система в данном случае дважды статически неопределима (иногда добавляют: «внутренним образом»).

В раме рис. 4, а и б также имеются внутренние дополнительные связи. Контур рамы полностью замкнут. Разрезая его в любом сечении (рис.5 в), мы, не нарушая кинематической неизменяемости, получаем возможность при заданных силах найти внутренние силовые факторы в каждом сечении рамы. Следовательно, разрезая замкнутую раму, мы снимаем дополнительные связи, т.е. позволяем сечениям А и В поворачиваться и смещаться в двух направлениях друг относительно друга. Обобщая, можно сказать, что замкнутый плоский контур имеет три дополнительные взаимные связи— трижды статически неопределим. Таким образом, рама, показанная на рис. 4, а, трижды статически неопределима. Рама, показанная на рис. 4, б, пять раз статически неопределима (три раза внутренним образом и два раза — внешним).

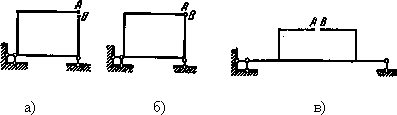
а) кинематически неизменяемая, б) неопределимая внутренним образом, в)со снятием дополнительных связей

Рис.5. Классификационные признаки рам:

Рассмотрим теперь несколько примеров определения степени статической неопределимости стержневых и рамных систем. На рис. 6 показано несколько рам. Последовательно рассмотрим их.

а) Рама имеет четыре дополнительные внешние связи и три взаимные связи, т. е. семь раз статически неопределима.

б) Полагаем сначала, что шарнир А отсутствует. Тогда имеются две внешние и три внутренние дополнительные связи. Система без шарнира А была бы пять раз статически неопределимой.

Шарнир А принадлежит одновременно трем стержням. Его можно рассматривать как два совпавших шарнира (рис. 7). Так как каждый шарнир снимает одну связь, т. е. разрешает поворот одного сечения относительно другого, то можно сказать, что шарнир А снимает две связи. Система становится, таким образом, вместо пяти — три раза статически неопределимой.

Обобщая сказанное, можно сделать вывод, что шарнир снимает число связей, на единицу меньшее числа сходящихся в нем стержней. В данном случае в шарнире А сходятся три стержня и шарнир снимает две связи.

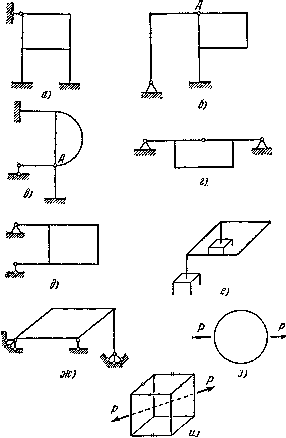
а) статически неопределимая — семь, б) — три, в) — четыре, г) — три, е) — двенадцать,
ж) — семь, д) — три, и) — тринадцать раз статически неопределима

Рис.6. Примеры рамных конструкций:

в) Если бы шарнир А отсутствовал, система была бы четыре раза внешним образом и три раза внутренним образом статически неопределимой, т. е. всего семь раз. Шарнир А снимает число связей, на единицу меньшее числа сходящихся в нем стержней, т. е. три связи. Рама четыре раза статически неопределима.

г) Рама три раза статически неопределима.

д) Внешние связи не удовлетворяют условиям кинематической неизменяемости. Это — механизм, точнее говоря, мгновенный механизм. Система имеет возможность поворачиваться относительно верхней опоры как жесткое целое Понятно, что угол поворота будет небольшим. Нижняя связь заклинится и будет достигнуто какое-то положение равновесия, но новое положение связей будет зависеть от жесткости системы. К раме неприменимы основные принципы сопротивления материалов: принцип неизменности начальных размеров и принцип независимости действия сил.

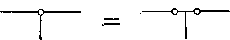
Рис.7. модель двух совпадших шарниров

е) Рама — пространственная. Имеется шесть дополнительных внешних связей (лишняя заделка) и шесть дополнительных взаимных связей (замкнутый контур) Система 12 раз статически неопределима.

ж) Система семь раз статически неопределима (один раз внешним образом и шесть раз — внутренним).

з) Здесь для плоской рамы не показаны внешние связи, но дана система внешних сил, удовлетворяющая условиям равновесия. В таком случае условились считать, что дополнительных внешних связей нет, и положение рамы в пространстве считается определенным; рассматриваются только внутренние связи. Система три раза статически неопределима.

и) Здесь также рассматриваются только внутренние связи, поскольку система указанных внешних сил удовлетворяет условиям равновесия. Нужно подсчитать, сколько сечений необходимо сделать в раме, чтобы, с одной стороны, она не «рассыпалась», а с другой, чтобы в ней не осталось ни одного замкнутого контура. Таких сечений следует сделать пять (см. рис. 6, и). Система 30 раз статически неопределима.

Лекция № 38. Метод сил.

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.

Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.

а-д) модификации основной системы
Рис.1. пример стержневой рамы:

Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а), б),..., которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,— с другой.

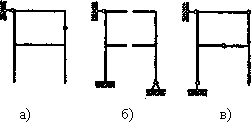
Рис.2.Некорректные преобразования заданной системы в основные по причине кинематической изменяемости- а) б), или статической определимости во всех узлах — в)

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X_i-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X_i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

а)-д) по отношению к заданной системе
Рис.3. Пять разновидностей основных систем

Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы. На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.

Теперь остается составить уравнения для определения неизвестных.

Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.

Перейдем теперь к составлению уравнений для определения неизвестных силовых факторов. Условимся через 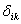обозначать взаимное смещение точек системы.

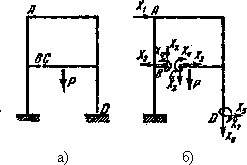
Рис.4. Пример расчета рамы а)по выбранной основной системе- б)

Первый индекс при 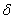соответствует направлению перемещения, а второй — силе, вызвавшей это перемещение.

В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:

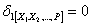
Индекс 1 означает, что речь идет о перемещении по направлению силы Х₁, а индекс [Х₁, Х₂,..., Р] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать:

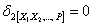
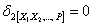
Так как под величиной 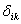понимается взаимное смещение точек, то 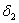обозначает вертикальное смещение точки В относительно С, 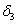— горизонтальное взаимное смещение тех же точек, 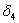есть взаимное угловое смещение сечений В и С. Угловым смещением будет также в рассматриваемой системе величина .

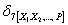В точках A и D смещения 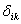являются абсолютными. Но абсолютные смещения можно рассматривать как смещения, взаимные с неподвижными отброшенными опорами. Поэтому принятые обозначения приемлемы для всех сечений системы.

Пользуясь принципом независимости действия сил, раскроем выражения для перемещений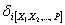

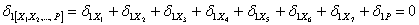
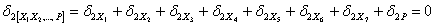
Аналогичным образом запишем и остальные пять уравнений: каждое из слагаемых 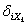, входящих в уравнение, обозначает перемещение в направлении силы с первым индексом под действием силы, стоящей во втором индексе. Поскольку каждое перемещение пропорционально соответствующей силе, величину 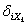можно записать в следующем виде:

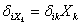
Что касается перемещений 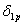, 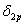и т. д., то под индексом Р будем понимать не просто внешнюю силу Р, а вообще систему внешних сил, которая может быть произвольной Поэтому величины 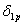, ,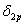... в уравнениях оставим неизменными.

Теперь уравнения примут вид:

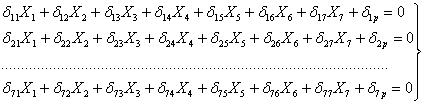
Эти уравнения являются окончательными и носят название канонических уравнений метода сил. Число их равно степени статической неопределимости системы. В некоторых случаях, как увидим далее, когда имеется возможность сразу указать значения некоторых неизвестных, число совместно решаемых уравнений снижается. Остается теперь выяснить, что представляют собой коэффициенты 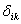и как следует их определять. Для этого обратимся к выражению (6.1).

Если 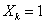, то

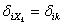
Следовательно, коэффициент 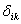это есть перемещение по направлению i-го силового фактора под действием единичного фактора, заменяющего k-й фактор. Например, коэффициент 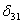уравнения представляет собой взаимное горизонтальное смещение точек B и С, которое возникло бы в раме, если бы к ней вместо всех сил была приложена только единичная сила в точке А (рис. 5 а). Если, например, вместо сил 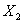приложив единичные силы, а все прочие силы с эквивалентной системы снять (рис. 5 б), то угол поворота в сечении D под действием этих сил будет 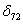, горизонтальное перемещение в точке А будет 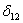и т. д.

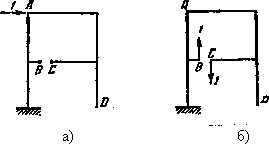
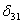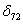а) , б) и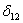
Рис.5. Интерпретация коэффициентов уравнений метода сил:

Весьма существенно отметить, что в проделанном выводе совершенно не обусловливается то, каким образом возникают перемещения 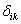. Хотя мы и рассматриваем раму, работающую на изгиб, все сказанное с равным успехом может быть отнесено, вообще, к любой системе, работающей на кручение, растяжение и изгиб или на то, другое и третье совместно.

Обратимся к интегралам Мора. Для того чтобы определить величину 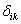, следует вместо внешних сил рассматривать единичную силу, заменяющую k-й фактор. Поэтому внутренние моменты и силы 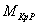, , 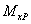, , 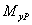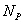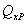и 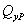в интегралах Мора заменим на 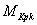, , 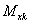, , 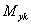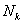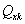и 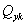, понимая под ними внутренние моменты и силы от единичного k-го фактора. В итоге получим:

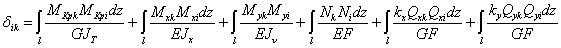
где 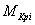, 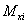… — внутренние моменты и силы, возникающие под действием i-го единичного фактора. Таким образом, коэффициенты 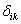получаются как результат перемножения i-го и k-го внутренних единичных силовых факторов. Индексы i и k непосредственно указывают, какие факторы должны быть перемножены под знаком интегралов Мора. Если рама состоит из прямых участков и можно пользоваться правилом Верещагина, то 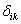представляет собой результат перемножения i-х единичных эпюр на k-е единичные эпюры.

Очевидно, что

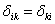
Это следует, с одной стороны, непосредственно из выражений для 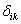, а с другой стороны, из теоремы о взаимности перемещений, поскольку перемещения 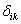и 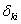возникают под действием одной и той же силы, равной единице.

Величины 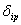, входящие в канонические уравнения, представляют собой перемещения в направлениях 1, 2,..., возникающие под действием заданных внешних сил в эквивалентной системе. Они определяются перемножением эпюры моментов заданных сил на соответствующие единичные эпюры.

Пример Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 6.

Рис.6. Заданная расчетная схема

Рама три раза статически неопределима. Выбираем основную систему, отбрасывая левую заделку. Действие заделки заменяем двумя силами 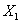, 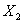и моментом 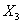и определяем эквивалентную систему (рис. 7).

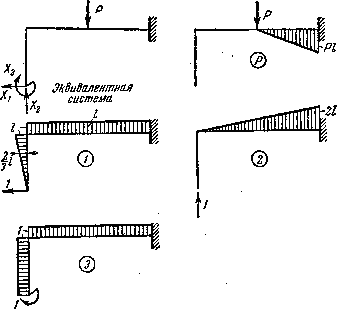
Рис.7. Динамика решения: от эквивалентной системы и силовой эпюры Р, включая эпюры моментов от единичных сил: 1, 2, 3 в точках приложения неизвестных , ,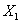

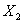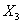
Канонические уравнения (6.2) принимают для рассматриваемой системы такой вид:

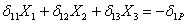
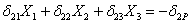
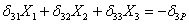
Основные перемещения в рассматриваемой раме определяются изгибом. Поэтому, пренебрегая сдвигом и сжатием стержней, строим эпюры изгибающих моментов от заданной силы P и от трех единичных силовых факторов (рис. 7).

Определяем коэффициенты уравнений, считая, что жесткость на изгиб всех участков рамы постоянна и равна EJ. Величина 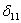определяется перемножением первой единичной эпюры самой на себя. Для каждого участка берется, следовательно, площадь эпюры и умножается на ординату этой же эпюры, проходящую через ее центр тяжести:

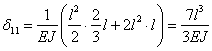
Заметим, что величины 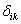при 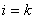всегда положительны, поскольку площади эпюр и ординаты имеют общий знак.

Определяем, далее, и остальные коэффициенты уравнений, перемножая эпюры с соответствующими номерами:

, , , , , , , .

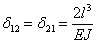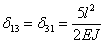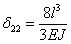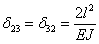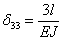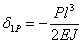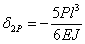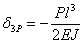Подставляем найденные коэффициенты в канонические уравнения. После сокращений получаем:

, ,

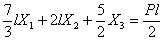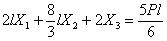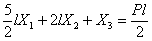
Решая эти уравнения, находим:

, ,

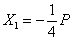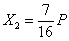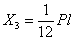
Раскрытие статической неопределимости на этом заканчивается.

Рис.8. Суммарная эпюра изгибающих моментов.

Эпюра изгибающих моментов может быть получена наложением на эпюру моментов заданных сил трех единичных эпюр, увеличенных соответственно в 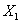, 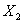и 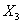раза Суммарная эпюра изгибающих моментов представлена на рис. 8. Там же пунктиром показана форма изогнутой оси рамы.

Лекция № 39. Расчет толстостенных цилиндров.

В тонкостенных цилиндрических резервуарах, подвергнутых внутреннему давлению, вполне возможно при вычислениях считать напряжения равномерно распределенными по толщине стенки. Это допущение мало отзывается на точности расчета.

В цилиндрах, у которых толщина стенок не мала по сравнению с радиусом, подобное предположение повело бы к большим погрешностям. Расчет таких цилиндров дан Ляме и Гадолиным в 1852 — 1854 гг. Работы русского академика А. В. Гадолина в области расчета кривых стержней в применении к расчету прочности артиллерийских орудий создали ему мировую известность. Отечественные артиллерийские заводы (и многие зарубежные) до сих пор проектируют и изготовляют орудия, пользуясь исследованиями Гадолина.

На Рис.1 изображено поперечное сечение толстостенного цилиндра с наружным радиусом 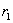, внутренним 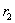; цилиндр подвергнут наружному 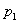и внутреннему давлению .

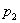Рис.1. Расчетная схема толстостенного цилиндра.

Рассмотрим очень узкое кольцо материала радиусом 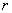внутри стенки цилиндра. Толщину кольца обозначим 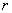. Пусть АВ изображает небольшую часть этого кольца, соответствующую центральному углу .

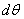Размер выделенного элемента, перпендикулярный к плоскости чертежа, возьмем равным единице. Пусть 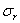и 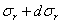будут напряжения, действующие по внутренней и наружной поверхностям элемента АВ, a 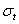— напряжения по его боковым граням. По симметрии сечения цилиндра и действующей нагрузки элемент АВ перекашиваться не будет, и касательные напряжения по его граням будут отсутствовать. По граням элемента AB, совпадающим с плоскостью чертежа, будет действовать третье главное напряжение 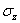, вызванное давлением на днище цилиндра. Это напряжение можно считать постоянным по всем точкам поперечного сечения цилиндра.

На элемент AB действуют в плоскости чертежа две силы 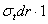coставляющие между собой угол 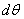, и радиальная сила, равная

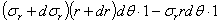
Эта сила направлена в сторону наружной поверхности. Уравновешиваясь, эти три силы составляют замкнутый треугольник abc (Рис.2).

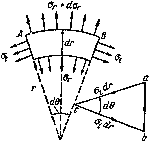
Рис.2. Условия равновесия элемента кольца

Из него следует, что радиальная сила, изображаемая отрезком ab, связана с силой 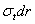(отрезок са) соотношением

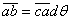
или

;

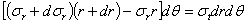пренебрегая малыми высшего порядка, получаем:

;

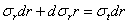отсюда

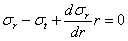(1)

Условие равновесия дало только одно уравнение для нахождения двух неизвестных напряжений. Задача статически неопределима, и необходимо обратиться к рассмотрению деформаций. Деформация цилиндра будет заключаться в его удлинении и в радиальном, перемещении всех точек его поперечных сечений. Назовем радиальное перемещение точек внутренней поверхности рассматриваемого элемента через u (Рис.3). Точки наружной поверхности переместятся по радиусу на другую величину 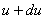; таким образом, толщина dr выделенного элемента увеличится на du, и относительное удлинение материала в радиальном направлении будет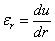

Рис.3. Геометрическая модель деформации элемента кольца

В направлении напряжений 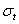относительное удлинение 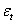будет равно относительному удлинению дуги ab, занявшей положение cd; так как относительное удлинение дуги таково же, как относительное удлинение радиуса r, то 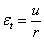. По закону Гука

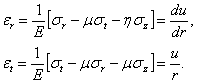(2)

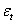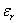Так как и определяются одной и той же функцией и 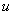то они связаны условием совместности. Дифференцируем 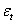по r:

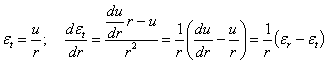(3)

Это и будет условие совместности деформаций; заменяя в нем значения 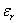и 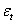по (2), получим второе уравнение, связывающее 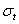и :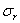

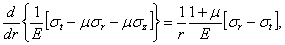
или

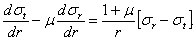(4)

Подставляя в это уравнение значение разности 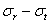из (32.1), находим:

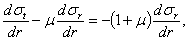
или

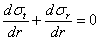(5)

Для совместного решения уравнений (1) и (5) продифференцируем первое по 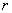и подставим в него значение 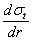из второго; получим:

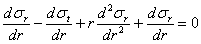
отсюда дифференциальное уравнение задачи:

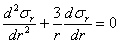(6)

Интеграл этого уравнения будет

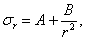(7)

что можно проверить подстановкой.

Постоянные А и В определятся из условий на внутренней и наружной поверхностях цилиндра:

(8)

Знак минус в правых частях этих формул поставлен потому, что положительными 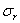мы приняли растягивающие напряжения (Рис.1).

Из условий (8) получаем:

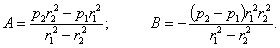
Пользуясь этими значениями и уравнением (7), получаем окончательные формулы для 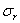и :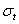

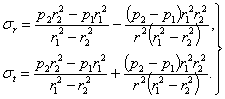(9)

Как видно из этих формул, сумма 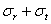( не зависит от r, т. е. относительная деформация вдоль оси цилиндра во всех точках сечения одинакова (так как и 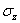одинаково), и сечение остается плоским

Представляет очень большой практический интерес случай когда имеет место только одно внутреннее давление 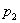; тогда

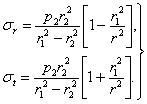(10)

График, изображающий распределение напряжений по толщине цилиндра в случае 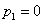, дан на Рис.3. Так как по абсолютной величине продольное растягивающее напряжение 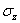обычно значительно меньше 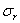и 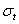то прочность цилиндра определяется этими последними. Применяя третью теорию прочности (наибольших касательных напряжений), получаем, что наибольшая разность главных напряжений, равная (для случая )

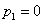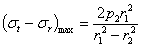(11)

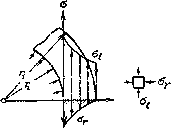
Рис.3. Распределение напряжений по толщине цилиндра при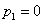

будет иметь место в точках внутренней поверхности цилиндра и всегда будет по абсолютной величине значительно больше внутреннего давления.

Таким образом, остаточные деформации появятся прежде всего у внутренней поверхности цилиндра, когда 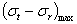будет равно пределу текучести материала; борьба с их появлением путем увеличения наружного радиуса 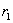практически безнадежна, — с увеличением 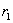растут и числитель, и знаменатель формулы (11); поэтому разность главных напряжений 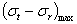хотя и убывает, но очень медленно. Однако момент появления пластических деформаций у внутренней поверхности цилиндра далеко не соответствует исчерпанию грузоподъемности конструкции; для правильной оценки прочности цилиндра необходимо перейти к расчету по допускаемым нагрузкам.

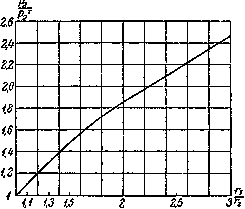
Рис.4. Динамика зоны текучести по толщине цилиндра

Полное исчерпание грузоподъемности произойдет тогда, когда кольцевая пластическая зона, распространяясь от внутренней поверхности цилиндра, дойдет до наружной; состояние разрушения наступит тогда, когда материал у наружной поверхности достигнет состояния, при котором произойдет разрыв. На фиг. 544 показано отношение внутреннего давления 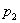, при котором пластическая зона охватывает все сечение, к давлению, соответствующему началу пластических деформаций 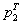. Оказывается,