Перевод чисел из 10-й системы счисления в другую СС.

Правило. Чтобы перевести число из одной системы счисления в другую, необходимо исходное число разделить на основание новой системы счисления. Полученное частное вновь поделить на основание новой системы счисления, и выполнять деление до тех пор. пока частное не будет меньше основания новой системы счисления. Полученные остатки от деления, начиная с последнего, записываются в обратном порядке. Это и будет запись числа в новой системе счисления.

Пример. Число 135 перевести из 10-тичной СС в 2-ичную, 8-ричную и 16-ричную системы счисления.

1)

2)

3)

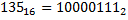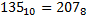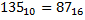Задание 2.

Перевести в двоичную, восьмеричную и шестнадцатеричную СС следующие числа 1275,973, 172

Обратный перевод чисел из любой СС в 10-тичную.

Правило.

1) Чтобы перевести число из любой СС в исходную СС (обратный перевод), нужно каждую цифру этого числа умножить на основание исходной СС. начиная с нулевой цифры справа налево, и произведения сложить. Если переводится десятичная дробь, следует применить правило для записи целой и дробной части числа.

2) Обратный перевод чисел осуществляется по формуле:

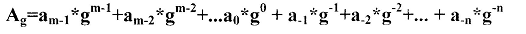
где A – заданное число,

g – основание СС заданного числа (=2 для 2-ичной СС, для других СС - подобно),

m – число цифр в целой части числа.

n – число цифр в дробной части числа,

a – значение цифр заданного числа(запись дробной части числа выделена синим цветом).

Пример:

110110₂= 1*2⁵+1*2⁴+0*2³+1*2²+1*2¹+0*2⁰=54₁₀

66₈=6*8¹+6*8⁰=48+6=54₁₀ 9A₁₆=9*16¹+10*16⁰=144+10=154₁₀

13,4₈=1*8¹+3*8⁰+4*8^-1=8+3+0.5=11.5₁₀ (это число – десятичная дробь)

Задание3.

Перевести в десятичную СС следующие числа:

101,11₂=5,75₁₀ 1011001₂ 1011,101₂

125,7₈=86₁₀ 1253₈ 175,132₈

A19BA₁₆=2585726…₁₀ 16A3₁₆ 2BAFD₁₆

Перевод чисел с основанием, являющимся степенью числа 2 и обратный перевод. К таким СС относятся двоичная, восьмеричная, шестнадцатеричная системы счисления.

Правило. Перевод из двоичной СС в восьмеричную СС. Двоичное число делится на группы по 3 цифры с конца(справа налево) и каждая группа преобразуется числом в новом СС

10.000.101₂=205₈

111.000.101.100₂=7054₈

1.011.001.101₂=1315₈

Правило. Для обратного преобразования каждая восьмеричная цифра записывается в виде триады.

Правило. Из двоичной СС в шестнадцатеричную СС: аналогично, но отделяем по 4 цифры

0110.0110.1011₂=66B₁₆

1011.1111.0111₂=BF7₁₆

10.1010.0111.0001₂=2A71₁₆

Правило. Для обратного преобразования каждая шестнадцатеричная цифра записывается в виде тетрады.

Перевод правильных и неправильных дробей в разных СС. Если нужно перевести обыкновенную дробь, то сначала ее нужно перевести в десятичную дробь, а затем применить правила перевода десятичных дробей.

Правило. Перевод десятичных дробей, меньших единицы (правильные дроби).

1) необходимо отделить вертикальной чертой дробную часть;

2) умножить дробную часть на основании новой системы счисления;

3) результат записать строго под исходным числом, начиная с младшего разряда; если получится перенос в целую часть, то записать ее слева от черты;

4) умножение дробной части проводится до тех пор пока не будет получено число с заданной точностью, либо справа от черты не будет 0.

0,728₁₀=0,564₈

Задание 4. Перевести из десятичной СС в двоичную, восьмеричную, шестнадцатеричную СС следующие правильные дроби: 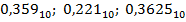.