Числовые характеристики системы двух случайных величин.

Начальным моментом порядка (k,s) системы (X,Y) называется математическое ожидание произведения X^k на Y^s:

α_k,s = M [X^kY^s].

Центральным моментом порядка (k,s) системы (X,Y) называется математическое ожидание произведения k –й и s-й степеней соответствующих центрированных величин:

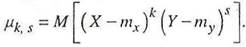
Для дискретных случайных величин начальные и центральные моменты вычисляются, соответственно, по формулам:

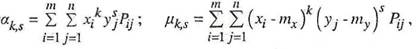
где P_ij = P(X = x_i; Y = y_j) – вероятность того, что система (X,Y) примет значения (x_i;y_j), а суммирование распространяется по всем возможным значениям случайных величин X, Y.

Для непрерывных случайных величин:

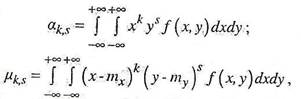
где f(х,у) – плотность распределения системы (X,Y).

Очевидно, что

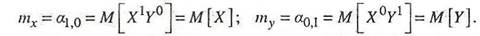
Совокупность математических ожиданий m_x и m_y представляет собой характеристику положения центра системы (X,Y).

Геометрически это координаты средней точки на плоскости, вокруг которой происходит рассеяние всех точек (X,Y).

ДисперсиивеличинX и Y характеризуют рассеяние случайной точки в направлении осей OX и OY:

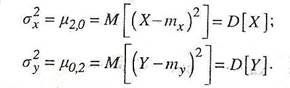
Особую роль как характеристики системы играет второй смешанный центральный момент

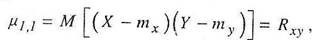
то есть математическое ожидание произведения центрированных величин.

Это ковариационный момент (корреляционный момент) случайных величин X, Y.

Для дискретных случайных величин корреляционный момент выражается формулой:

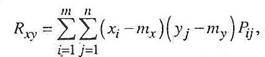
а для непрерывных –

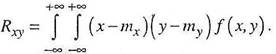
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеяния величин Xи Y, еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.

Для характеристики степени тесноты связи между величинами (X, Y)в чистом виде переходят от момента R_xy к безразмерной характеристике

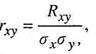
где σ_х,σ_y- средние квадратические отклонения величин Xи Y.

Эта характеристика называется коэффициентом корреляциивеличин Xи Y.

Коррелированными называют две случайные величины, если их корреляционный момент (или коэффициент корреляции) отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.

Две независимые случайные величины всегда являются некоррелированными. Обратное верно не всегда.

Равенство нулю коэффициента корреляции (корреляционного момента) есть необходимое, но недостаточное условие независимости случайных величин. Условие независимости случайных величин — более жесткое, чем условие некоррелированности.

Коэффициент корреляции характеризует степень тесноты только линейной зависимости между случайными величинами.

Свойства коэффициента корреляции:

1)r_xy = r(X,Y)= r(aX +b, cY + d), где а, b, с, d- константы;

2) -1 ≤ r_xy ≤ 1.

Вопросы для повторения

1. Поясните условия, при которых на практике возникает закон Пуассона.
2. Поясните условия, при которых на практике возникает закон нормального распределения.
3. Поясните условия, при которых на практике возникает закон равномерного распределения.
4. Поясните условия, при которых на практике возникает закон показательного распределения.

Резюме по теме

На практике встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала. В пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.

Биномиальным называют закон распределения дискретной случайной величины Х - числа появлений события в п независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна р (вероятность непоявления события также постоянна и равна q=1 - р). При этом вероятность возможного значения X = m, где m - число появлений события в n испытаниях, вычисляется по формуле Бернулли.