Баланса энергии для невязкой жидкости
В невязкой жидкости отсутствуют силы внутреннего трения и, следовательно, рассеивание энергии при движении, поэтому запас
 энергии в единице массы движущейся жидкости постоянен. При движении кроме объемных и поверхностных сил в жидкости действуют и силы инерции. В соответствии с принципом Даламбера для единицы массы жидкости уравнение движения может быть получено, если к проекциям массовых и поверхностных сил (2.3) прибавить с обратным знаком проекции сил инерции, отнесенные к единице массы
энергии в единице массы движущейся жидкости постоянен. При движении кроме объемных и поверхностных сил в жидкости действуют и силы инерции. В соответствии с принципом Даламбера для единицы массы жидкости уравнение движения может быть получено, если к проекциям массовых и поверхностных сил (2.3) прибавить с обратным знаком проекции сил инерции, отнесенные к единице массы
j = PJm:
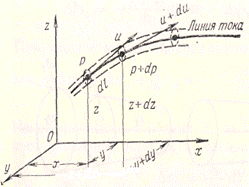
Рис 14.1. Схема к выводу уравнения
Эйлера к проекциям массовых и
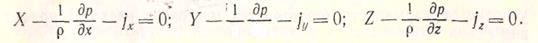
При установившемся движении
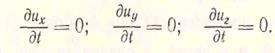
Подставив значения проекций jx, jy и jz из систмемы (3.2), получим уравнения движения Эйлера:
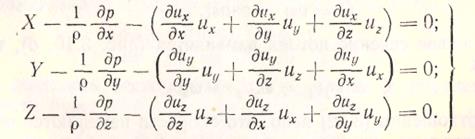 (3.24)
(3.24)
Мерой движения жидкости является энергия, измеряющаяся работой, которую может совершить жидкость при торможении (кинетическая энергия), и работой, которую могут совершить массовые и поверхностные силы (потенциальная энергия) при переходе от рассматриваемого положения в пространстве к нулевому (для последнего потенциальная энергия условно считается равной нулю). Следовательно, для получения уравнения энергии необходимо найти работу, которую могут совершить силы при перемещении массы на отрезок dl по линии тока.
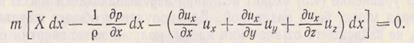 (3.25) (3.25) |
Умножив члены уравнения (3.24) на массу m и проекцию dl на ось х (рис. 4.1), получим дифференциальное уравнение энергии в проекциях на ось х
Выразим в последнем слагаемом уравнения (3.24) проекцию перемещения dx через скорость и время dx = ux dt и сделаем элементарные преобразования
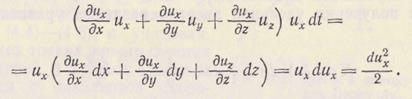
В уравнении (3.25) последнее слагаемое представляем в виде 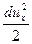 и по аналогии для других осей
и по аналогии для других осей 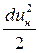 и
и 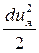
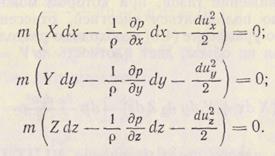
Сложив почленно эти уравнения, получим выражение для полной энергии
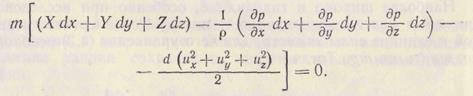
Так как выражение в скобках являются полными дифференциалами
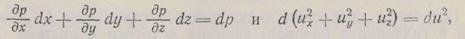
из сис
то окончательно уравнение энергии будет
m (X dx + У dy + Z dz - 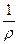 dp -
dp - 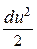 ) = 0. (3.26)
) = 0. (3.26)
Все члены уравнения (4.3) имеют размерность энергии:
[ m (X dx + У dy + Z dz] = 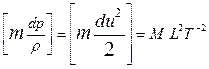
единица в системе СИ — джоуль (Дж); 1 Дж = 1 Н -м.
В уравнение (3.25) входит величина перемещающейся массы т, которая может быть различной. Для получения общего выражения, не зависящего от значения массы, полный запас энергии относят к единице массы, объема или силы тяжести.
Энергия, отнесенная к единице массы, называется удельной энергией е и широко используется при исследовании движения газов с переменной плотностью. Для получения удельной энергии разделим уравнение (3.26) на т:
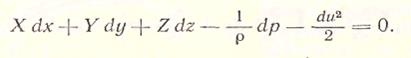 (3.27)
(3.27)
Размерность всех членов этого уравнения: L2T2, единица в системе СИ - Дж/кг = м2/с2 (квадрат скорости).
Исследуя движение газов, при котором можно считать р = const, удобно пользоваться энергией, отнесенной к единице объема, для чего уравнение (3.26) необходимо разделить на объем V. Масса, деленная на объем, дает плотность m/V = р и уравнение примет вид ,
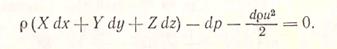 (3.28)
(3.28)
Размерность членов этого уравнения ML-2Т 2.
Все члены уравнения выражают давление, единица которого в системе СИ – Дж/м3 = Н/м2 = Па.
Наиболее широко в гидравлике, особенно при исследовании движения капельных жидкостей, пользуются энергией, отнесенной к единице силы тяжести, для чего уравнение (3.26) необходимо разделить на mg. Тогда
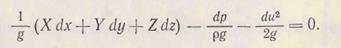 (3.29)
(3.29)
Все члены уравнения имеют размерность длины L, называемой в гидравлике напором, единица которого в системе СИ -Дж/Н =м.
Напор выражается высотой в метрах столба движущейся жидкости.
