Дифференциальные уравнения равновесия жидкости

Выделим вокруг точки А, находящейся внутри покоящейся жидкости, элементарный объем в виде параллелепипеда с ребрами dx, dy, dz, параллельными произвольно выбранным в пространстве осям координат (рис. 2.3). Отбросим мысленно ,окружающую параллелепипед жидкость, заменив ее действие на грани соответствующими силами гидростатического давления.

Пусть давление жидкости в точке А равно 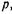, тогда давление

на грани 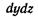будет: на левую 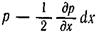, на правую _,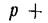

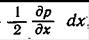где 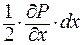— приращение давления вдоль оси Ох на расстоянии dx/2

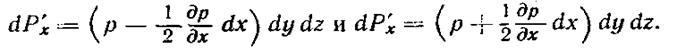Элементарные силы давления на грани 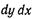будут соответственно равны: Аналогичным образом можно найти элементарные силы, дей 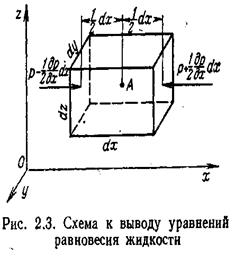ствующие на остальные четыре грани (на рисунке показаны только давления, действующие вдоль оси Ох).

Кроме поверхностных сил на выделенный объем действуют также массовые силы, результирующая которых в общем случае будет

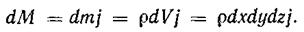
Спроектируем все действующие на элементарный объем силы на ось Ох и приравняем сумму этих проекций нулю;

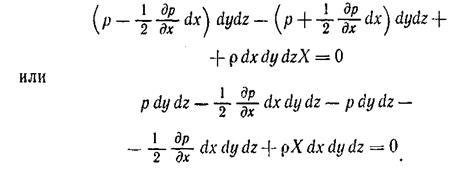
После приведения подобных и сокращения оставшихся слагаемых на 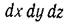получим Спроектировав остальные силы на оси Оу и Oz и сделав аналогичные преобразования, получим систему уравнений:

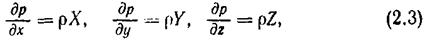
из которых видно, что. приращение гидростатического давления в направлении какой-либо координатной оси возможно только при наличии ускорения в этом направлении и происходит за счет массовых сил. Эти уравнения представляют собой общие условия равновесия жидкости в дифференциальной форме, выведенные в 1755 г. Л. Эйлером.

Для приведения уравнений Эйлера к виду, удобному для интегрирования, умножим каждое из уравнений (2.3) соответ­ственно на dx, dy, dz и сложим почленно:

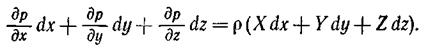
В этом уравнении левая часть представляет собой полный дифференциал давления dp, поэтому

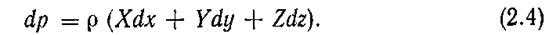
Полученное уравнение выражает функциональную зависимость давления от рода жидкости и координат точки в пространстве

и позволяет определить значение давления в любой точке жидкости, находящейся в равновесии. Это уравнение справедливо для капельных жидкостей и для газов, причем для газов дополнительным условием равновесия является уравнение состояния (1.4).

Из выражения (2.4) можно легко получить уравнение поверхности равного давления — поверхности, давление во всех точках которой одинаково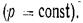

При p= const dp=0, а так как ρ не может быть равно нулю, следовательно,

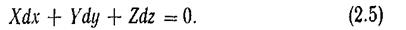
Уравнение (2.5) — уравнение поверхности равного давления, частным случаем которой является свободная поверхность жидкости.

Рассмотрим несколько конкретных примеров и установим, какой вид будет иметь поверхность равного давления (в том числе и свободная поверхность) в этих случаях.

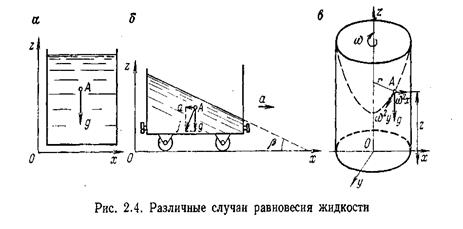
Пример. Жидкость находится в равновесии в резервуаре в поле действия только силы тяжести (рис. 2.4, а).

В этом случае проекции результирующей единичных массовых сил будут:

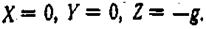
Подставляя эти значения в (2.5), получим

-a ^.dx – gdx = 0

или после интегрирования

Это — уравнение горизонтальной плоскости. Следовательно, в покоящейся однородной жидкости r =i dem любая горизонтальная плоскость является плоскостью равного давления.

Пример. Жидкость находится в равновесии в резервуаре, движущемся горизонтально с некоторым ускорением а (рис. 2.4, б).

В этом случае любая частица жидкости находится под действием ускорений а и g, следовательно, проекции результирующей единичных массовых сил будут:

Подставляя 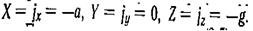эти значения в (2.5), получим 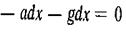или после интегрирования

Это — уравнение наклонной плоскости. Следовательно, в данном случае поверхности равного давления представляют собой плоскости, наклонные к осям Ох и Оz и параллельные оси Оу. Угол наклона плоскости к горизонту может быть найден из выражения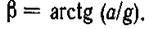

Пример. Жидкость находится в равновесии в цилиндрическом резервуаре, вращающемся вокруг вертикальной оси с постоянной угловой скоростью со (рис. 2.4, в).В этом случае любая частица жидкости находится под действием ускорений силы тяжести g и центробежной силы инерции 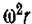, следовательно, проекции ре­зультирующей единичных массовых сил будут: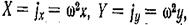

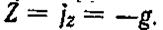Подставляя эти значения в уравнение (2.5), получим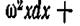 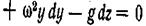или после интегрирования

Это — уравнение параболоида вращения. Следовательно, в данном случае поверхности равного давления представляют собой семейство параболоидов вращения вокруг вертикальной оси. При сечении их вертикальной плоскостью получится семейство парабол с вершинами на оси Оz, а при сечении горизонтальной плоскостью — семейство концентрических окружностей с центром на оси Оz.

В последних двух примерах рассмотрены случаи так называемого относительного покоя жидкости, когда она находится в резервуарах, движущихся тем или иным образом с постоянным ускорением, но частицы жидкости не перемещаются друг относительно друга и относительно стенок резервуара.