Методы составления цифровых моделей линейных устройств

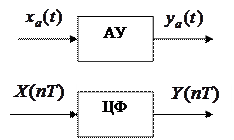
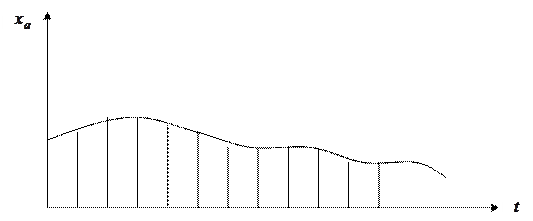
При цифровом моделировании АУ входной и выходной сигналы в модели представляются как решетчатые функции:

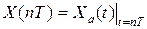
Идеальная цифровая модель обеспечивает

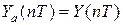при .

Пр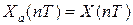актически обеспечивается

.

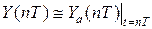Моделируемое устройство может быть описано, например, с помощью передаточной функции:

,

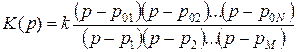где 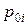- нули функции;

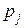- полюсы функции.

По 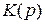можно определить импульсную характеристику. Если полюсы простые, то:

,

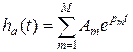где 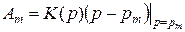- вычет

.

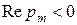Метод инвариантности импульсной характеристики

При использовании этого метода обеспечивается равенство (с точностью до коэффициента Т) импульсной характеристики цифровой модели и импульсной характеристики моделируемого устройства в дискретные моменты времени:

.

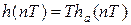Передаточная функция ЦМ может быть получена как Z-преобразование:

.

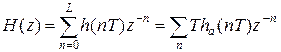Эта формула соответствует нерекурсивной схеме фильтра, где коэффициенты определяются как:

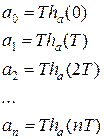
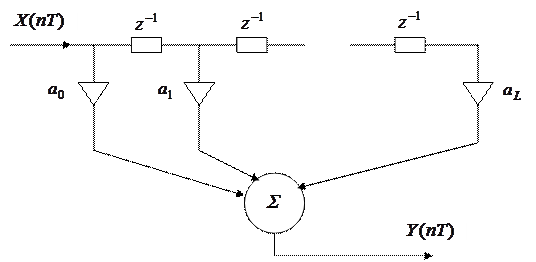Построение модели в виде нерекурсивного фильтра удобно в том случае, если число коэффициентов 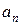, отличных от нуля, мало (т.е. импульсная характеристика моделируемого линейного устройства ограничена во времени (НЧ-фильтры)). В противном случае для построения модели надо взять ¥ число ячеек.

Можно использовать рекурсивный алгоритм вычислений.

Импульсная характеристика:

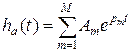
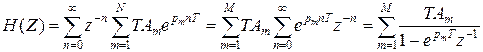(8)

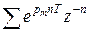- сумма членов геометрической прогрессии вида:

.

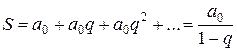
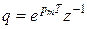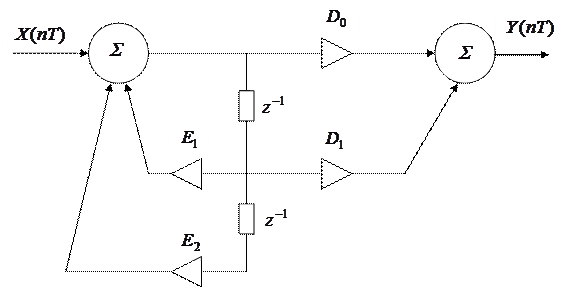
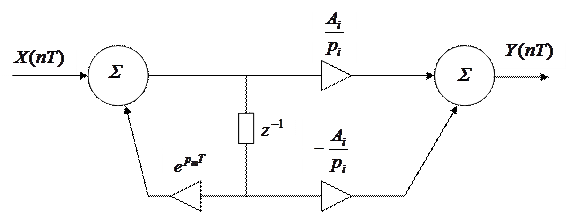
Если реализовать формулу (8) непосредственно, то получим схему вычислений в виде параллельного фильтра.

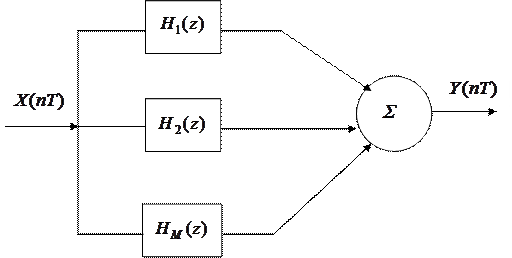Каждое звено в этой схеме – это рекурсивный фильтр.

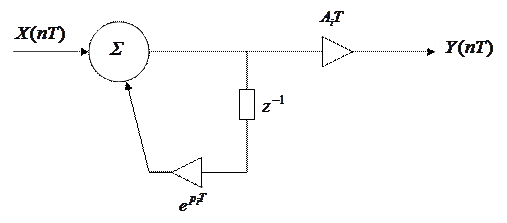Если 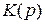имеет пару комплексно-сопряженных полюсов, то вычеты будут комплексно-сопряженными. 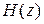могут быть представлены в этом случае в виде передаточной функции фильтра второго порядка с действительными коэффициентами

.

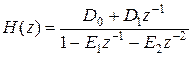Пример.

Разработать цифровую модель инерционного звена по методу инвариантности импульсной характеристики.

, .

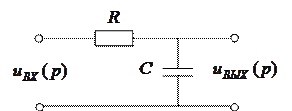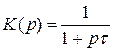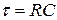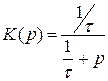
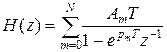
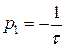
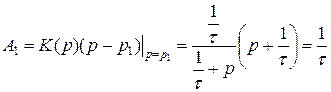
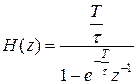
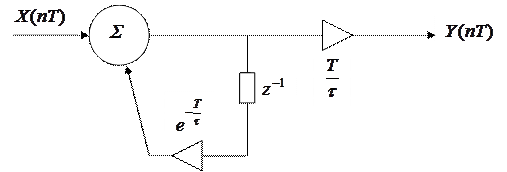В этом методе не гарантируется совпадение других характеристик.

Переходная характеристика моделируемой схемы (аналогового устройства):

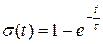
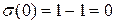
В нашей модели при подаче 1 в момент времени 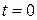получаем .

.

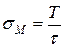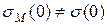Чтобы ошибка была меньше, нужно, чтобы .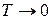

Метод ИИХ не может быть использован, когда 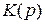не имеет полюсов, или когда число полюсов меньше или равно числу нулей.

Метод инвариантности переходной характеристики

При использовании этого метода обеспечивается равенство переходной характеристики цифровой модели и моделируемого устройства в дискретные моменты времени.

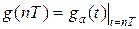
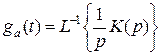
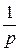- изображение скачка

Передаточная характеристика цифрового фильтра:

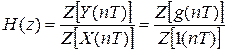
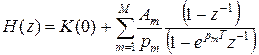(9)

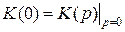
Формула (9) приводит к параллельной схеме вычислений:

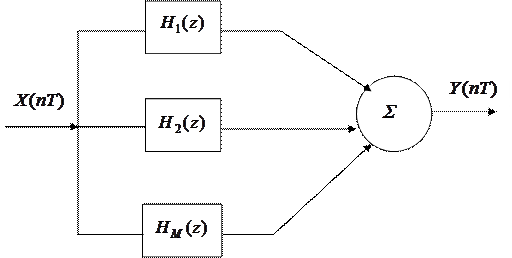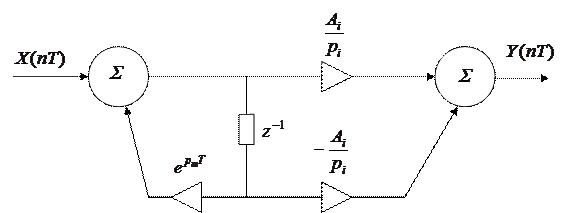Для :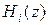

Пример.

Разработать цифровую модель инерционного звена по методу инвариантности переходной характеристики.

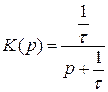
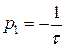
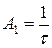
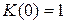
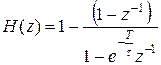
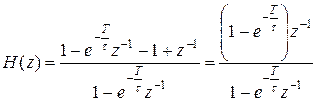
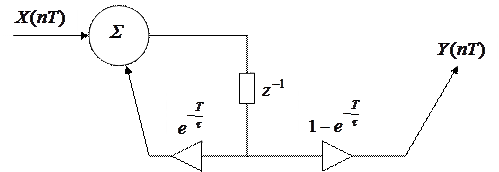Метод инвариантности переходной характеристики нельзя использовать, если 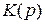не имеет полюсов или число полюсов меньше числа нулей.

Если число полюсов равно числу нулей, или 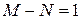, то частотные характеристики модели и аналогового устройства могут не совпадать.

Метод согласованного Z-преобразования

До сих пор в Z-плоскости преобразовывались полюсы передаточной функции 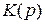, нули не использовались.

Представим 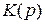в виде:

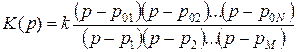
В этом методе множители вида 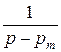преобразуются к виду 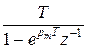, а множители вида 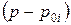- к виду .

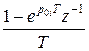Тогда передаточная функция 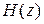имеет вид:

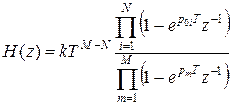
Или для перехода от 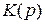к 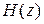осуществляется замена каждого множителя вида

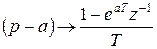
Пример.

Разработать ЦМ инерционного звена методом согласованного Z-преобразования.

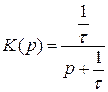
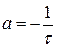Þ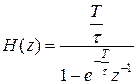

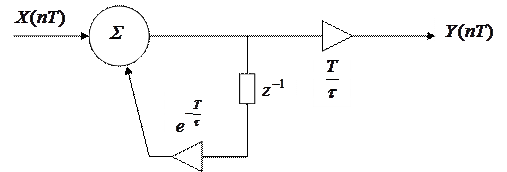Если функция не имеет полюсов, то можно использовать только метод согласованного Z-преобразования.

Пример.

Получить ЦМ идеального дифференциатора.

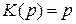
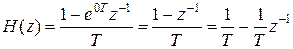
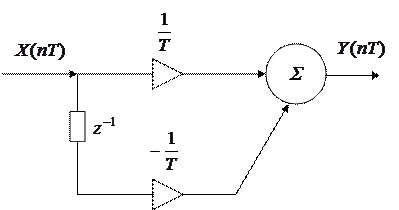Рассмотрим в качестве аналогового устройства пропорционально-интегрирующий фильтр.

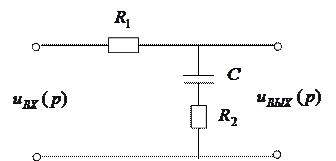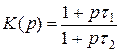
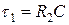
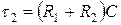
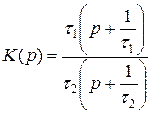
Будем сопоставлять АЧХ устройства и модели.

А) При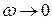

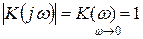
Б) При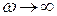

;

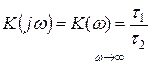
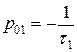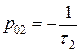
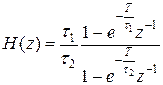
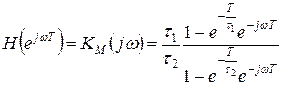
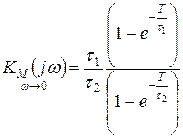
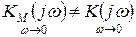
Если шаг дискретизации уменьшать:

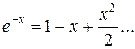
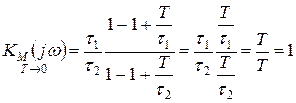
При .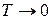

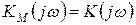Как уже отмечалось, если передаточная функция 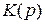не имеет полюсов, то использовать можно только метод согласованного Z-преобразования. Однако метод часто может дать различие частотных и временных характеристик, если нули передаточной функции имеют действительную часть, превышающую величину .

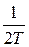Метод не всегда гарантирует близкое совпадение характеристик модели и моделируемого устройства, если 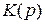не имеет нулей.

Метод билинейного Z-преобразования

Метод заключается в нахождении 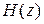по 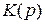с помощью замены:

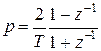
Пример.

Разработать ЦМ инерционного звена методом билинейного Z-преобразования.

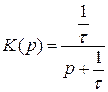
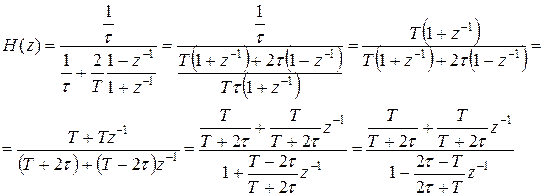
Основное достоинство метода заключается в том, что применение этого метода гарантирует хорошее совпадение ЧХ в области частот

.

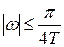Если число нулей больше числа полюсов, то модель – неустойчива.