Преимущества цифрового моделирования по сравнению с аналоговым

Метод несущей

Применяется для моделирования высокочастотных и низкочастотных звеньев на основе принципиальной схемы, схемы замещения, функциональной или структурной схем; при преобразовании сигнала в звене с помощью спектрального, временного методов или при описании с помощью дифференциальных уравнений.

Особенностью метода является моделирование входных сигналов и помех с точностью до мгновенных значений напряжений и токов. Модель в этом случае наиболее соответствует прототипу.

Сигнал моделируют по формуле:

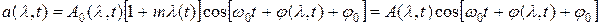l - информационный параметр

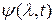- сведения об угловой модуляции

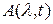- сведения об амплитудной модуляции

m – глубина модуляции.

Примеры.

1. Модель амплитудного детектора при описании его на основе принципиальной схемы.

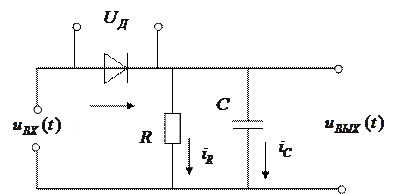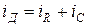
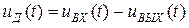
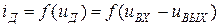- безынерционное нелинейное преобразование

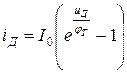
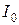- тепловой ток

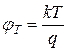- температурный потенциал

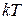- тепловая энергия

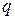- заряд

;

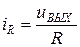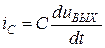
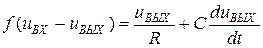
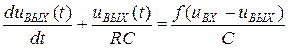
Это – дифференциальное уравнение первого порядка, нелинейное, которое может быть решено на ЭВМ стандартными методами при подстановке .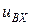

Модель апериодического усилителя на основе схемы замещения.

Схема замещения

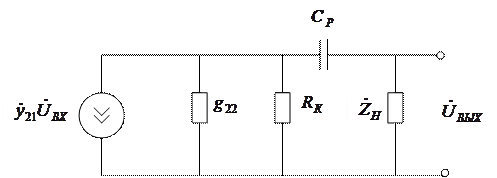Коэффициент передачи для всей области частот:

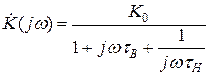
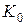( - коэффициент передачи на средней частоте)

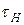- постоянная времени в области нижних частот

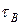- постоянная времени усилителя в области верхних частот (учитывает инерционные свойства).

Записываем коэффициент передачи в операторной форме:

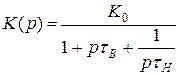
Изображение выходного напряжения:

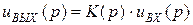
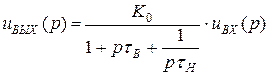
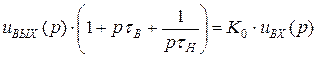
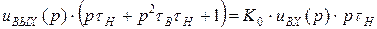
От изображения переходим к оригиналу, вспоминая, что умножение на р – операция дифференцирования.

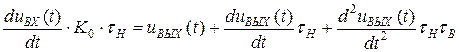
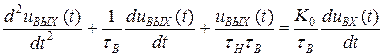
Получили линейное дифференциальное уравнение второго порядка, которое может быть решено на ЭВМ стандартными методами при задании .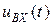

Модель фазового детектора на основе структурной схемы.

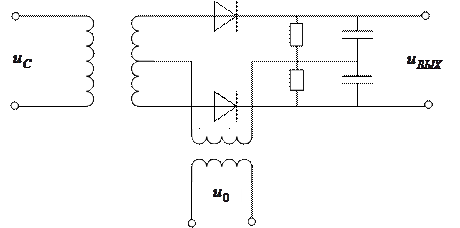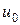- мгновенное значение опорного напряжения

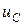- мгновенное значение сигнального напряжения.

ФД сравнивает фазу сигнального напряжения с фазой опорного напряжения.

.

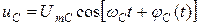
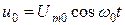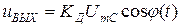
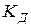- коэффициент передачи.

Перемножаем напряжения:

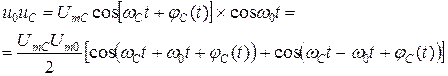
Разность частот 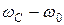практически равна 0.

На основе анализа последней формулы вытекает схема ФД.

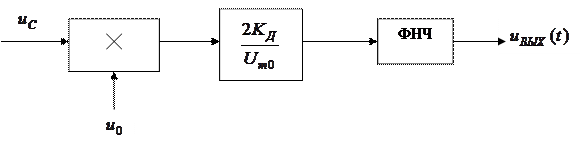ФНЧ – фильтр нижних частот (отфильтровывает частоты 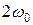и пропускает разностные частоты.

В качестве ФНЧ может быть использовано инерционное звено.

Описывается ДУ первого порядка.

Метод комплексной огибающей

Сущность метода сводится к замене реального р/звена моделью низкочастотного звена с входным воздействием в виде комплексной огибающей реального узкополосного сигнала. Метод применяется, как правило, при моделировании на основе принципиальных схем, структурных и функциональных схем. Метод применяется для узкополосных сигналов, у которых 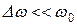( 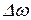- ширина спектра, 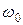- частота несущей).

Сигнал описывается следующим образом:

.

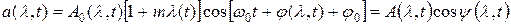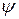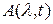В общем случае между и нет однозначного соответствия. Неоднозначность можно избежать введением комплексного или аналитического сигнала:

,

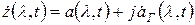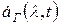- сигнал, сопряженный по Гильберту.

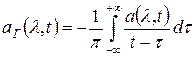
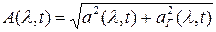(1)

.

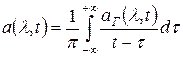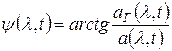(2)

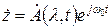
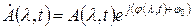
В 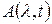заложена вся информация об АМ.

Ф-ла (1) является математической моделью идеального детектора, ф-ла (2) – мат. моделью идеального фазового детектора.

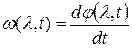(3)

Ф-ла (3) – математическая модель идеального фазового детектора.

При таком описании сигнала исключается множитель 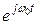, который является переносчиком информации.

Моделирование по методу комплексной огибающей сводится к разработке алгоритма, связывающего комплексные огибающие на входе и выходе.

Получаемая модель является низкочастотной, так как комплексная огибающая сигнала – это медленно меняющаяся во времени функция.

В методе экономится машинное время и память.

Моделирование процесса преобразования комплексной огибающей сигнала линейной цепью.

Сигнал на выходе связан с входным воздействием: (интеграл Дюамеля):

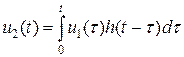(4)

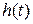- импульсная характеристика цепи.

Для низкочастотного эквивалента цепи можно записать:

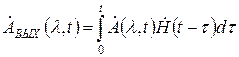(5)

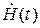- комплексная импульсная характеристика.

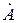- комплексная огибающая.

Комплексную огибающую на выходе линейной цепи можно промоделировать прямо по формуле (5) (в универсальной ЭВМ, где есть представление комплексных чисел).

В случае (5) по сравнению с (4) количество операций сложения и умножения будет больше. Можно разработать рекурентные соотношения, с помощью которых можно будет моделировать быстрее, но не точнее.

Если в ЭВМ нет представления комплексных чисел, то фильтр с импульсной характеристикой 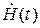можно будет промоделировать с помощью четырех фильтров, имеющих действительные импульсные характеристики.

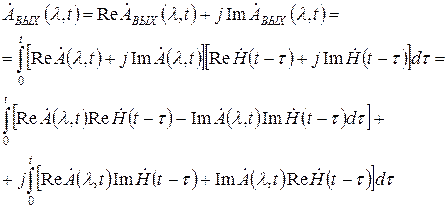
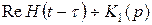
¸ - прямое преобразование Лапласа.

.

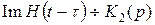Преимущества цифрового моделирования по сравнению с аналоговым

1. Большая точность расчетов. При цифровом моделировании всегда есть алгоритмическая и вычислительная ошибки. Они являются принципиальными, но могут быть уменьшены.

2. Более гибкое моделирование. Всегда можно учесть начальные условия.

3. Лучше развита логика.

4. Имеет место больший диапазон представляемых величин.

5. Совершеннее связь машина-человек.

6. Больший объем памяти и практически неограниченный срок хранения информации.

7. Удобство представления векторных величин.

У аналогового моделирования можно отметить простоту генерации электрических сигналов и помех и их фильтрацию в динамических системах.

Основные положения при переходе от описания объекта к его математической модели

1. Блочное представление модели;

2. Выделение главного при составлении модели;

3. Разбиение работы устройства на отдельные этапы и составление модели для каждого этапа в отдельности.

ФАПЧ: 1. вход в синхронизм;

2. работа в режиме синхронизации;

3. срыв слежения.

4. Разбиения всего диапазона изменения входных величин на отдельные интервалы и составление модели на интервалах.

5. Обеспечение эквивалентности модели и объекта.

На входе р/системы действует информационный параметр 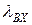, на выходе получаем оценку .

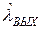Наиболее полным описанием является совместная многомерная плотность вероятности:

)

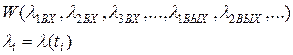Для модели:

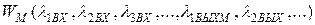
Входные l - одни и те же, а выходные l - разные для модели и объекта.

Полное описание, если .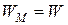

Простым и широко используемым критерием является равенство моментов первого порядка (мат. ожидания).

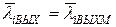
Для моментов второго порядка (корреляционных функций):

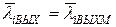
Этапы моделирования

1. Разработка математического описания объекта.

2. Разработка аналоговой или цифровой модели на основе математического описания.

3. Разработка программы для ЦВМ и реализация ее на машине.

4. Счет на машине по программе (машинное моделирование) и получение результата.

5. Обсуждение результата и возможно корректирование модели.

Классификация методов математического моделирования

1. На основе какой схемы осуществляется моделирование:

А) принципиальная схема;

Б) схема замещения;

В) структурная схема.

Г) Функциональная схема.

2. По типу звеньев: линейные и нелинейные, стационарные и нестационарные, инерционные и безынерционные, функциональные и нефункциональные.

Стационарные линейные звенья описываются с помощью линейных дифференциальных уравнений с постоянными коэффициентами, линейные нестационарные звенья описываются с помощью линейных дифференциальных уравнений с переменными коэффициентами.

Функциональные звенья – такие, в которых можно отдельно выделить инерционные блоки линейные и безынерционные блоки нелинейные.

3. По способу описания преобразования сигнала в звене:

а) с помощью ДУ;

б) используя спектральный метод или преобразование Лапласа;

в) используя временные методы (интеграл Дюамеля).

4. По способу описания сигнала:

А) Метод несущей. Используется для описания низкочастотного и высокочастотного сигнала).

,

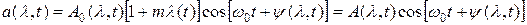l - информационный параметр

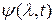- сведения об угловой модуляции

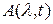- сведения об амплитудной модуляции

m – глубина модуляции.

Выборки берутся по теореме Котельникова.

Б) Метод комплексной огибающей.

Применяется для узкополосных сигналов и устройств. В этом случае

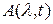- модуль комплексной огибающей сигнала

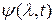- фаза комплексной огибающей.

При этом моделировании цепь является низкочастотной.

Запоминать нужно меньшее число отсчетов и необходим меньший объем памяти.

В) Метод информационного параметра:

- формульный метод;

- метод статистических эквивалентов;

- метод эквивалентов.

Формульный метод: аналитически удается получить функциональную связь:

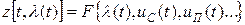
Метод статистических эквивалентов: оценка информационного параметра на выходе модели в статистическом смысле совпадает с оценкой информационного параметра на входе реального устройства.

Метод несущей

Применяется для моделирования высокочастотных и низкочастотных звеньев на основе принципиальной схемы, схемы замещения, функциональной или структурной схем; при преобразовании сигнала в звене с помощью спектрального, временного методов или при описании с помощью дифференциальных уравнений.

Особенностью метода является моделирование входных сигналов и помех с точностью до мгновенных значений напряжений и токов. Модель в этом случае наиболее соответствует прототипу.

Сигнал моделируют по формуле:

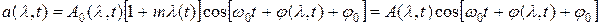l - информационный параметр

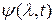- сведения об угловой модуляции

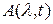- сведения об амплитудной модуляции

m – глубина модуляции.

Примеры.

1. Модель амплитудного детектора при описании его на основе принципиальной схемы.

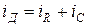
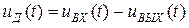
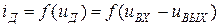- безынерционное нелинейное преобразование

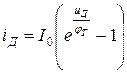
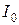- тепловой ток

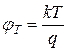- температурный потенциал

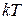- тепловая энергия

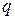- заряд

;

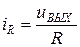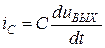
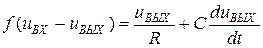
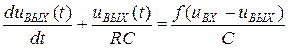
Это – дифференциальное уравнение первого порядка, нелинейное, которое может быть решено на ЭВМ стандартными методами при подстановке 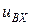.