Линейные системы с постоянными коэффициентами
Система линейных дифференциальных уравнений с постоянными коэффициентами (однородная или неоднородная) всегда может быть проинтегрирована путем сведения ее к одному уравнению высшего порядка.
Пример 1. Найти общее решение системы
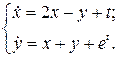
Решение.Продифференцируем первое уравнение системы: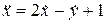 
. В правую часть полученного равенства подставим выражение для 
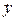из второго уравнения системы: 
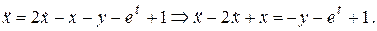Выразим 
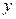из первого уравнения системы
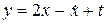(3.1)
Тогда для отыскания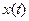 
получим неоднородное уравнение
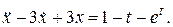
Корни характеристического уравнения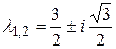 
. Поэтому общее решение соответствующего однородного уравнения имеет вид
.
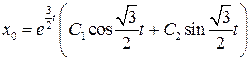Частное решение неоднородного уравнения ищем в виде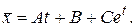 
Используя стандартные приемы, находим: 
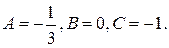Итак,
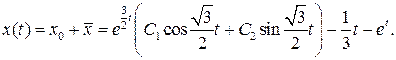
Используя формулу (3.1), получаем
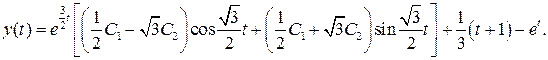
Изложенный метод удобен только для решения несложных систем. В общем случае для решения линейных систем может быть использован "матричный метод".
Пусть имеется линейная система
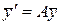, (3.2)
где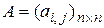 
постоянная матрица, 
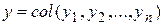. Обозначим через 
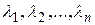собственные значения матрицы 
.
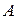Если все собственные значения матрицы различны, то общее решение системы (3.2) имеет вид
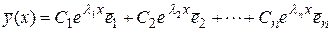, (3.3)
где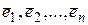 
собственные векторы, соответствующие указанным собственным значениям.
Пример 2.Найти общее решение системы
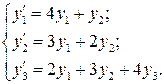
Решение. Составим характеристическое уравнение
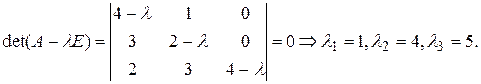
Ненулевые собственные векторы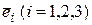 
, соответствующие найденным собственным значениям, могут быть найдены как алгебраические дополнения элементов любой строки матрицы 
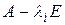. Так, например, в качестве собственного вектора, соответствующего собственному значению 
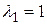, возьмем алгебраические дополнения элементов первой строки матрицы
.
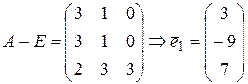Аналогично находим
.
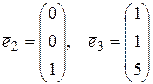Поэтому, согласно формуле (3.3), общее решение системы имеет вид
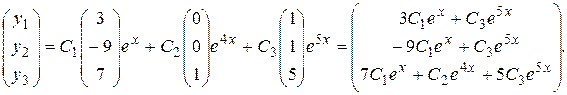
Если среди различных корней характеристического уравнения имеются комплексно-сопряженные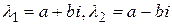 
, то каждой такой паре корней соответствуют два комплексных решения 
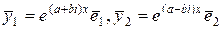, где 
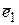и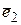 
– комплексные собственные векторы. Комбинируя эти решения, легко получить два решения в вещественной форме. В качестве таких решений можно взять 
, 
.
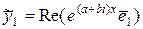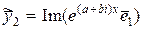Если среди корней характеристического уравнения имеется корень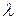 
кратности 
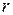, то этому корню соответствует решение вида
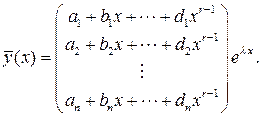(3.4)
Для нахождения значений неизвестных коэффициентов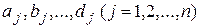 
нужно подставить выражение (3.4) в систему (3.2) и приравнять коэффициенты при одинаковых степенях 
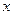в левой и правой частях получившихся равенств. При этом следует помнить, что ровно 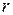из отыскиваемых коэффициентов могут быть выбраны произвольно, а остальные должны быть выражены через них.
Пример 3.Найти общее решение системы
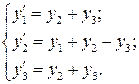
Решение.Характеристическое уравнение
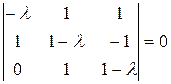или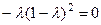 
.
имеет корни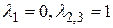 
.
Простому собственному значению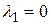 
соответствует собственный вектор 
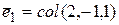и решение вида
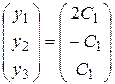. (3.5)
Решение, соответствующее двукратному корню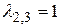 
, в соответствии с формулой (3.4), будем искать в виде
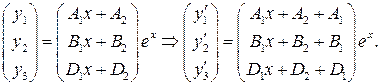
Получаем уравнение
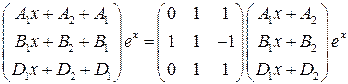
или
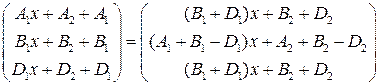
Приравнивая коэффициенты при одинаковых степенях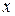 
в левой и правой частях последнего равенства, получим систему уравнений
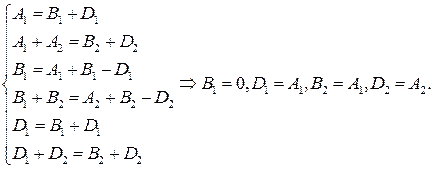
Считая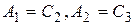 
произвольными постоянными, окончательно находим
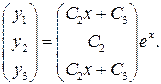
Складывая, наконец, последнее выражение с (3.5), получаем общее решение системы
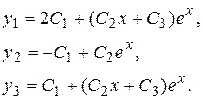
Матричная экспонента
Другой метод решения линейных систем с постоянными коэффициентами основан на использовании в качестве фундаментальной матрицы матричной экспоненты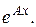 
Матрица 
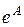определяется как сумма ряда
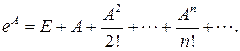
Если матрица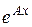 
найдена, то решение системы (3.1) с начальным условием 
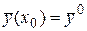имеет вид 
.
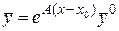Для отыскания матрицы 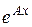могут быть применены различные приемы, в зависимости от структуры спектра матрицы 
.
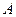I. Если все собственные значения 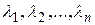матрицы 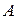– действительные различные числа, то матрицу 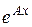удобно находить так:
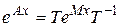, (3.6)
где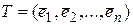 
(матрица, составленная из столбцов координат собственных векторов матрицы А), а
.
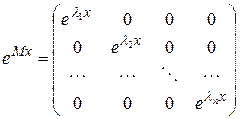II. Если среди различных собственных значений матрицы А имеются комплексные, то матрица 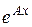в вещественной форме может быть найдена с помощью следующего приема: нужно найти общее решение системы (3.1) так, как это было описано выше, а потом составить матрицу, i-ым столбцом которой будет решение этой системы, удовлетворяющее начальным условиям 
, 
.
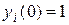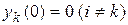Пример 4. Для матрицы системы из примера 2 найти .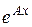
Решение.Составим матрицу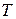 
из столбцов координат собственных векторов матрицы :
.
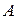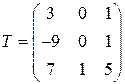Тогда
.
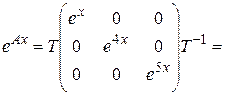
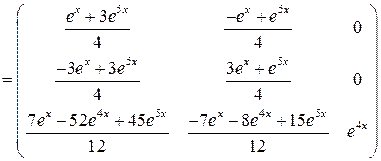Пример 5.Для матрицы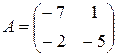 
найти .
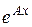Решение.Собственные значения матрицы 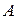– комплексно сопряженные числа 
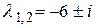. Собственный вектор, соответствующий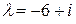 
.
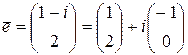Имеем:
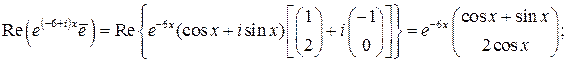
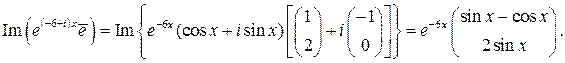
Поэтому общее решение линейной системы (3.2) с заданной матрицей 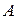имеет вид
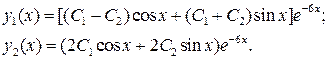
Найдем,сначалачастноерешение, удовлетворяющееусловию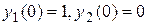 
. Оно будет иметь вид
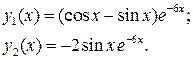
Частноерешение,удовлетворяющее условиям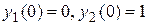 
,имеет вид
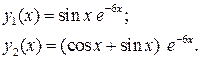
Поэтому
.
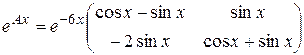III. Если среди собственных значений матрица 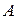имеются кратные, то следует отыскать матрицу 
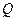, приводящую матрицу 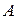к жордановой форме:
.
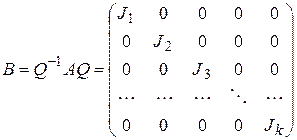Жордановаклетка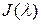
,соответствующаякорню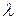кратности 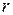,имеетвид
.
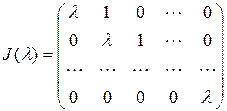Для такой клетки легко находится
. (3.7)
ПроведятакиепостроениядлякаждойклеткиЖордана, находим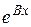
.Тогда
.
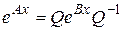Пример 6. Вычислить матрицу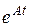 
, если 
.
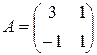Решение. Собственные значения данной матрицы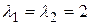 
. Так как ранг матрицы 
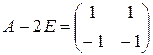равен 1, то жорданова форма матрицы А имеет вид 
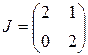. Матрицу 
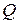, приводящую матрицу А к жордановой форме, найдем из уравнения 
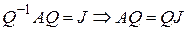. Пусть 
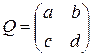. Тогда для отыскания элементов матрицы 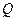получим уравнение
.
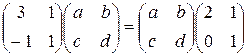Это матричное уравнение эквивалентно системе
,
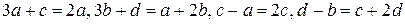решение которой следующее: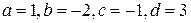 
. Итак,
.
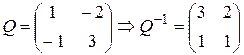Согласно формуле (3.7)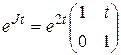 
. Поэтому
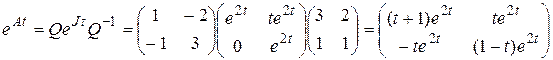(3.8)
Формула Коши
Решение неоднородной системы с постоянными коэффициентами
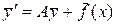, (3.9)
удовлетворяющее начальному условию 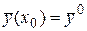, может быть выражено через экспоненциал матрицы системы по формуле
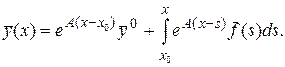(3.10)
Если решение системы (3.9) записано в виде (3.10), то говорят, что оно записано в форме Коши.
Пример 7. Найдя матрицу 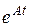, записать решение системы
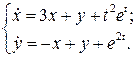
в форме Коши.
Матрица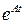 
для рассматриваемой системы уже была найдена в предыдущем примере, и она имеет вид (3.8). Согласно формуле (3.10), можем записать
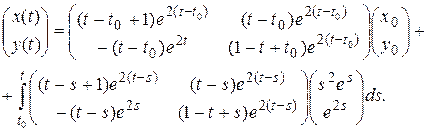
Задание 12
Решить линейную систему путем сведения ее к одному уравнению высшего порядка
1. 
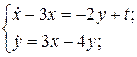
2. 
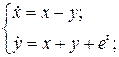
3. 
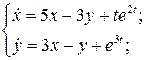
4. 
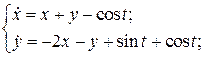
5. 
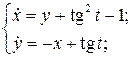
6. 
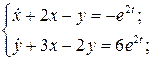
7. 
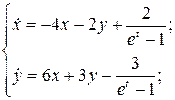
8. 
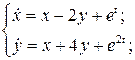
9. 
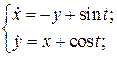
10. 
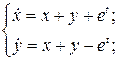
11. 
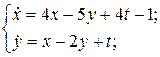
12. 
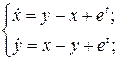
13. 
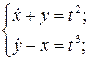
14. 
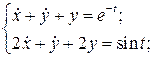
15. 
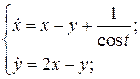
16. 
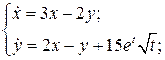
17. 
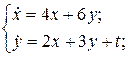
18. 
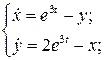
19. 
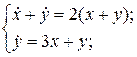
20. 
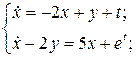
21. 
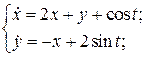
22. 
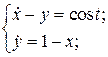
23. 
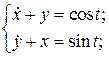
24. 
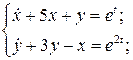
25. 
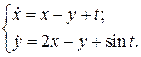
26. 
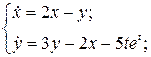
27. 
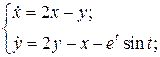
28. 
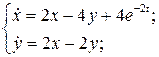
29. 
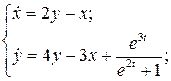
30. 
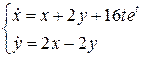
31. 
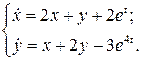
Задание 13
Решить систему матричным методом
1. 
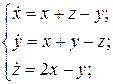
2. 
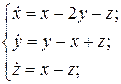
3. 
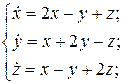
4. 
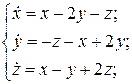
5. 
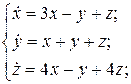
6. 
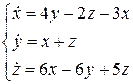
7. 
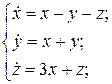
8. 
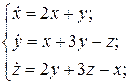
9. 
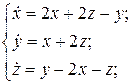
10. 
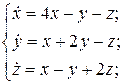
11. 
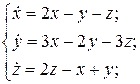
12. 
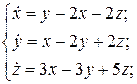
13. 
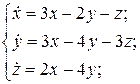
14. 
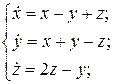
15. 
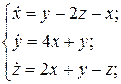
16. 
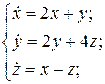
17. 
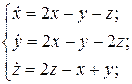
18. 
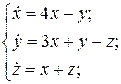
19. 
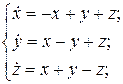
20.
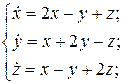
21. 
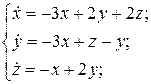
22. 
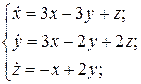
23. 
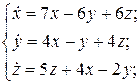
24. 
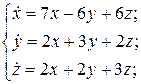
25. 
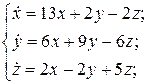
26. 
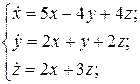
27. 
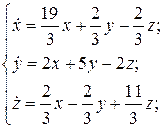
28. 
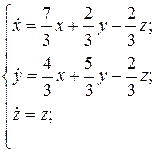
29. 
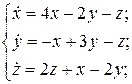
30. 
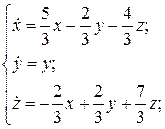
31. 
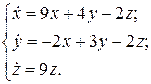
Задание 14
Найти 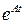, где А – матрица линейной части системы из задачи 12 и записать решение этой системы по формуле Коши.
Библиографический список
1. Агафонов, С.А. Дифференциальные уравнения: учебник для втузов/С.А.Агафонов, А.Д.Герман, Т.В.Муратова; под ред. В.С.Зарубина, А.П.Крищенко.— 4-е изд.,испр. — М.: Изд-во МГТУ им.Н.Э.Баумана, 2006.— 352 с.
2. Амелькин, В.В. Дифференциальные уравнения в приложениях/В.В.Амелькин.— М.: Едиториал УРСС, 2009.— 208 с.
3. Демидович, Б.П., Моденов, В.П. Дифференциальные уравнения/Б.П. Демидович, В.П. Моденов. — СПб.: Лань, 2006.— 288 с. — (Учебники для вузов. Специальная литература).
4. Егоров, А.И. Обыкновенные дифференциальные уравнения с приложениями/А.И. Егоров.— М.: ФИЗМАТЛИТ, 2007. — 448с.
5. Краснов, М.Л., Киселев, А.И., Макаренко, Г.И. Обыкновенные дифференциальные уравнения. Задачи и примеры с подробными решениями/М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. — М.: КомКнига, 2005.— 256 с. — (Вся высшая математика в задачах).
6. Кузнецов, Л.А. Сборник заданий по высшей математике: Типовые расчеты: учеб. пособие/Л.А. Кузнецов.— 9-е изд., стер.— Санкт-Петербург [и др.]: Лань, 2007.— 240 с. — (Учебники для вузов. Специальная литература).
7. Матвеев, Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям/Н.М. Матвеев.— СПб.: Лань, 2002. — 432 с. — (Учебники для вузов. Специальная литература).
8. Самойленко, А.М., Кривошея, С.А., Перестюк, Н.А. Дифференциальные уравнения. Практический курс/А. М. Самойленко, С.А. Кривошея, Н.А. Перестюк. — М.: Высшая школа, 2006. — 384 с.
9. Треногин, В.А. Обыкновенные дифференциальные уравнения/В.А. Треногин. — М.: ФИЗМАТЛИТ, 2009. — 312 с.
10. Федорюк, М.В. Обыкновенные дифференциальные уравнения/М.В. Федорюк. — М.: Либроком, 2009. — 448 с.
11. Филиппов, А.Ф. Сборник задач по дифференциальным уравнениям/А.Ф. Филиппов. — М.: Либроком, 2013. — 240 с. — (Классический учебник МГУ).
12. Эльсгольц, Л.Э. Дифференциальные уравнения/Л.Э. Эльсгольц. — М.: ЛКИ, 2013. — 312 с. — (Классический учебник МГУ).
[1] Все задачи в данном задании сводятся к уравнениям с разделяющимися переменными.