Тема 9. Математическое программирование.

1. Уметь построить область допустимых планов, которая задается системой линейных уравнений и неравенств.

2. Уметь построить вектор-градиент целевой функции и линию нулевого уровня.

3. Знать различные формы записи задачи линейного программирования (ЗЛП).

4. Уметь переходить от одной формы ЗЛП к другой.

5. Знать алгоритм симплекс-метода.

6. Знать критерий оптимальности решения ЗЛП на максимум.

7. Уметь для ЗЛП, заданной в симметричной форме, построить двойственную ей задачу.

8. Уметь построить начальный опорный план транспортной задачи (ТЗ) методом северо-западного угла и методом минимального элемента.

9. Знать критерий оптимальности решения ТЗ.

10. Уметь перейти к нехудшему опорному решению ТЗ.

Задачи для самостоятельного выполнения

ЗЛП решить графически:

1.

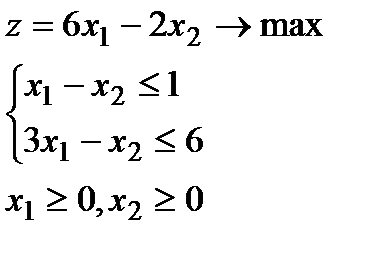
2.

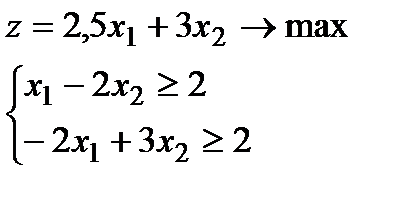
3.

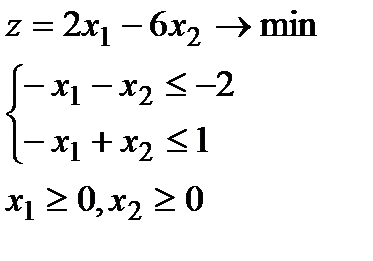
4.

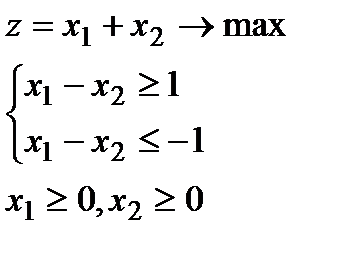
5.

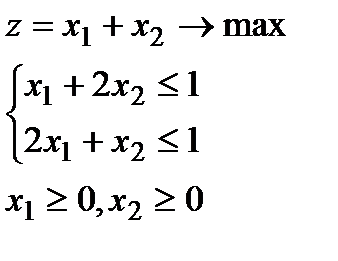
ЗЛП решить симплекс-методом:

1. 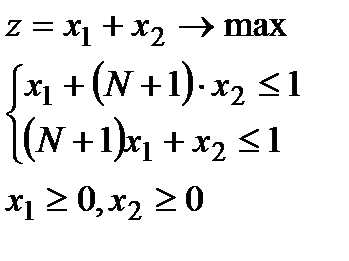(здесь 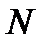- номер студента по списку)

Для приведённых ЗЛП написать двойственную:

1.

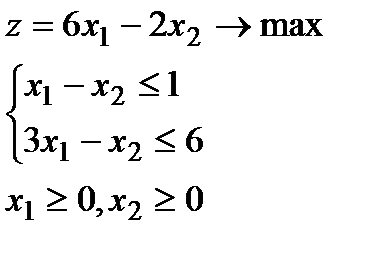
2.

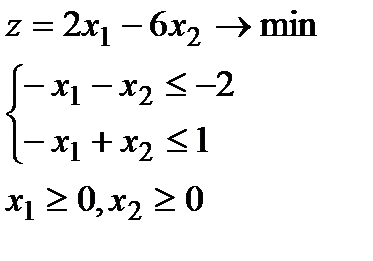
3.

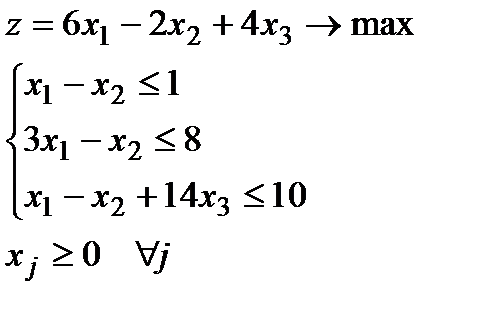
4.

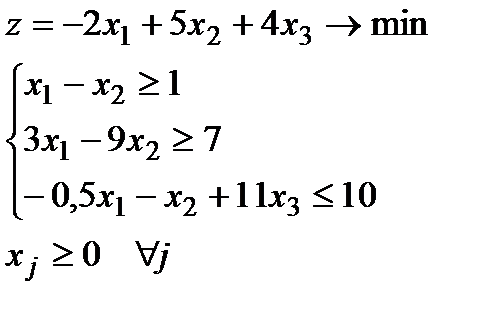
5.

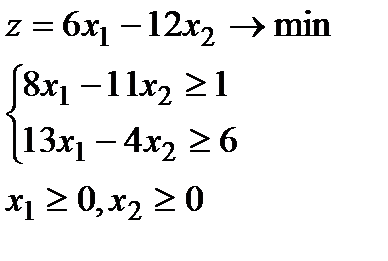
Составить первоначальный план ТЗ методом северо-западного угла и(или) методом минимального элемента по следующим данным:

1 Таблица 9.1

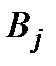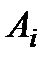2 Таблица 9.2

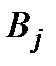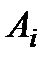3 Таблица 9.3

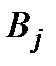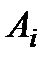4 Таблица 9.4

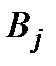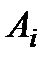5 Таблица 9.5

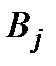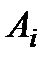Образцы решения ЗЛП:

Задание 1

Решить задачу линейного программирования графическим методом

;

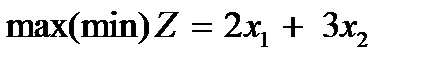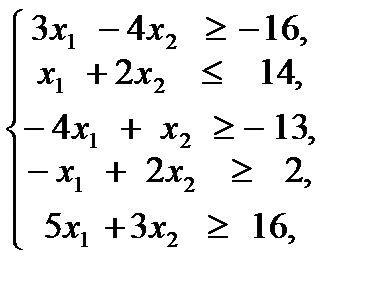
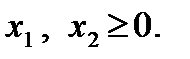
Решение

1. Построим область допустимых решений. Для этого запишем уравнения сторон многоугольника допустимых решений, положив в ограничениях вместо неравенств равенства

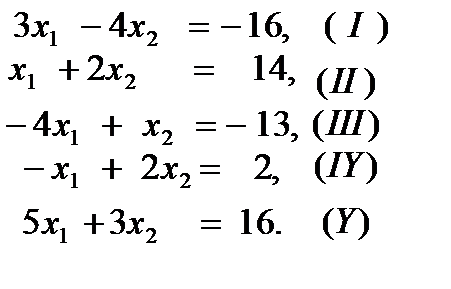
Строим прямые, определяемые уравнениями (I) – (Y) и определяем полуплоскости, удовлетворяющие исходным неравенством. Пересечение этих полуплоскостей образует пятиугольник АВСDE.

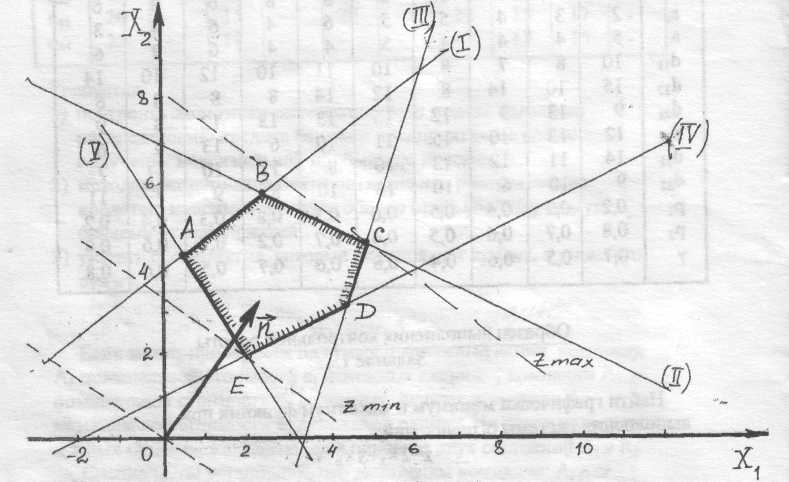Рисунок 6 – Область допустимых решений

2. Строим вектор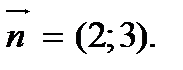

3. Проводим линию нулевого уровня 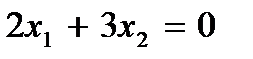, перпендикулярную вектору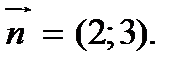

4. Перемещаем линию нулевого уровня в направлении вектора 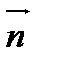. Первая точка контакта линии уровня с пятиугольником АВСDE является точка Е и, следовательно, 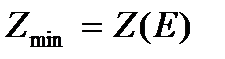. Последняя точка контакта – точка С и, следовательно, .

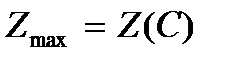5. Найдем координаты точек Е и С.

Е – точка пересечения прямых (IY) и (Y).

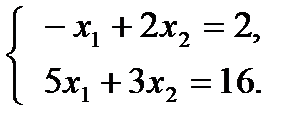
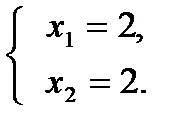
Е(2; 2), 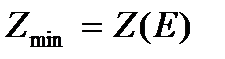= Е(2; 2) = .

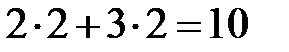С – точка пересечения прямых (III) и (II).

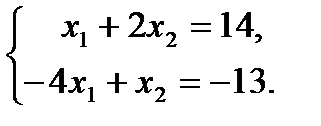
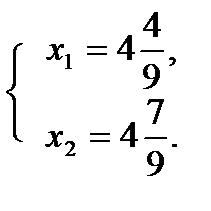
С ( 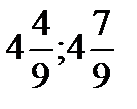), 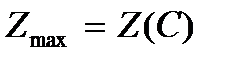= Z ( ) =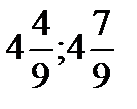

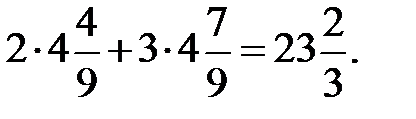
Ответ: .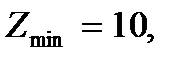

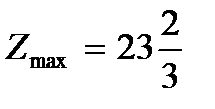Задание 2

Для изготовления 4-х видов продукции используют три вида сырья. Количество сырья вида 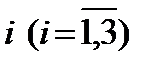, необходимое для изготовления единицы продукции вида 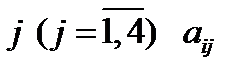, запасы сырья 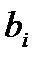и прибыль от реализации единицы продукции вида 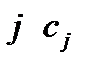заданы матрицей

= .

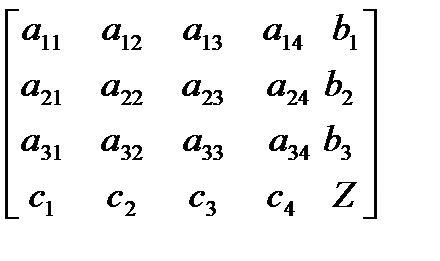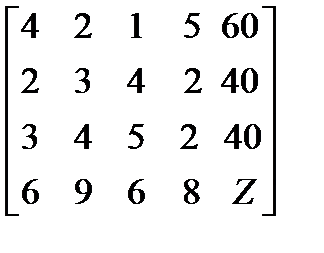Требуется:

1) составить экономико-математическую модель задачи, пользуясь которой, можно найти план выпуска продукции, при котором общая прибыль 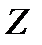будет наибольшей;

2) симплексным методом найти оптимальный план выпуска продукции и максимальную величину прибыли;

3) составить задачу, двойственную к исходной, и пояснить ее экономическую суть. Используя теорию двойственности, установить соответствие между переменными прямой и двойственной задач, найти двойственные оценки;

4) с помощью двойственных оценок исследовать:

а) степень полезности отдельных видов ресурсов в условиях производства;

б) величину финансовых потерь в расчете на единицу продукции в случае, если предприятие вынуждено будет производить невыгодные ему виды продукции. При необходимости такого производства обосновать цены на готовую продукцию.

Решение

1) Составим экономико-математическую модель задачи. Обозначим через Х₁, Х₂, Х_3, Х₄ количество весовых единиц четырех видов продукции, которые планируется изготовить. Тогда прибыль, полученная от реализации выпущенной продукции, будет равна:

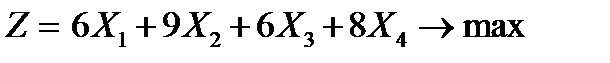(9. 1)

Переменные 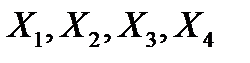должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов сырья, что выражается неравенствами:

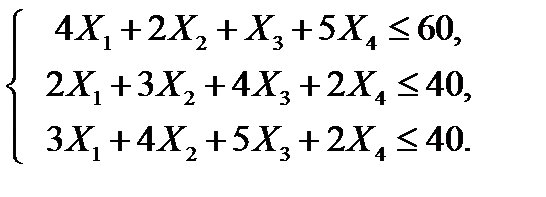(9. 2)

По смыслу задачи

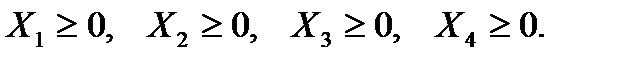(9. 3)

Таким образом, условия (9. 1) – (9.3) определяют экономико-математическую модель поставленной задачи.

2) Решим задачу линейного программирования (9.1)–(9.3) симплексным методом. Для этого перейдем к канонической форме записи задачи линейного программирования, введя дополнительные (балансовые) переменные 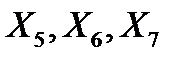, которые означают возможные остатки ресурсов сырья:

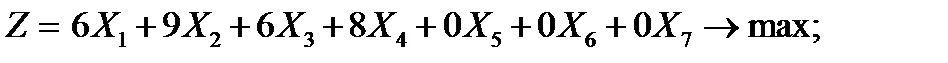(9. 1′)

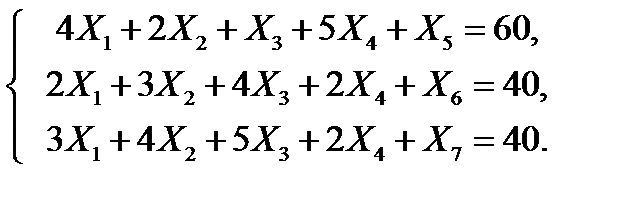(9. 2′)

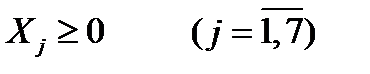. (9. 3′)

Составим начальную симплексную таблицу по данным математической модели (9. 1′)–(9. 3′).

Таблица 9.6

БП	СБ	Ао	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Θ
Х5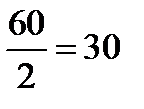
Х6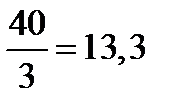
Х7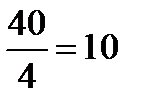
Zj–Cj		–6	–9	–6	–8

Этой симплексной таблице соответствует опорный план 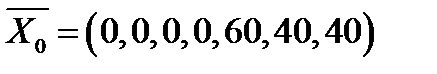, который не является оптимальным, так как в индексной строке Z_j–C_j есть отрицательные элементы. Построим новый опорный план, более близкий к оптимальному. Для этого выполним симплексные преобразования таблицы 1. Наибольший по модулю отрицательный элемент индексной строки (–9) указывает на то, что переменную 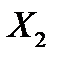надо ввести в число базисных переменных (т.е. столбец, соответствующий переменной 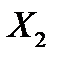, берем в качестве разрешающего). Чтобы определить переменную, которую необходимо вывести из числа базисных, составляем симплексные отношения и выбираем наименьшее из них:

.

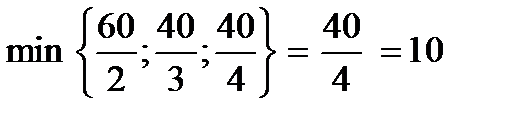Следовательно, из базиса выводим переменную Х₇, а соответствующий столбец называем разрешающим. На пересечении разрешающего столбца и разрешающей строки находится разрешающий (ключевой) элемент 4. С помощью разрешающего элемента выполняем симплексные преобразования, которые приводят к таблице 9.7.

Таблица 9.7

БП	СБ	Ао	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Θ
Х5			2,5		–1,5				–0,5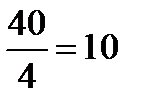
Х6			–0,25		0,25	0,5			–0,75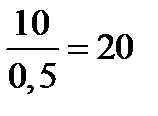
Х2			0,75		1,25	0,5			0,25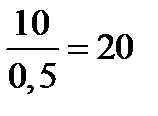
Zj–Cj		0,75		5,25	–3,5			2,25

Полученный опорный план 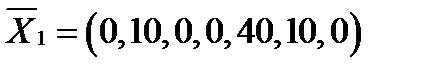не является оптимальным, так как в индексной строке есть отрицательный элемент (–3,5), который соответствует переменной Х₄ (а соответствующий столбец будет разрешающим). Определим разрешающую строку, выбрав из симплексных отношений наименьшее:

.

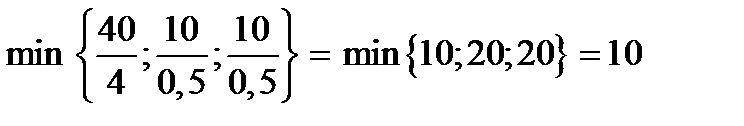Таким образом, в качестве разрешающей строки необходимо взять строку, соответствующую переменной Х₅. Это означает, что базисную переменную Х₅ необходимо заменить свободной переменной Х₄. Проводя симплексные преобразования, мы придем к таблице 9.8.

Таблица 9.8

БП	СБ	Ао	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Θ
Х4
Х6
Х2
Zj-Cj		2,94		3,94		0,88		1,81
		Y4	Y5	Y6	Y7	Y1	Y2	Y3

В полученной симплексной таблице в индексной строке нет отрицательных элементов, поэтому опорный план 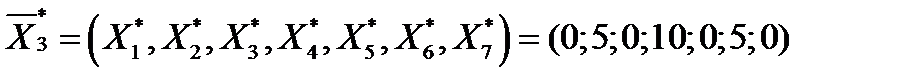является оптимальным, он является единственным, так как все индексные оценки свободных переменных больше 0.

Вывод. Максимальная возможная прибыль предприятия (в имеющихся условиях) будет 125 денежных единиц, если оно произведёт 5 единиц измерения продукции 2-го вида и 10 единиц измерения продукции 4-го вида, а продукцию 1-го и 3-го видов вообще выпускать не будет. При таком плане производства ресурсы 1-го и 3-го видов будут израсходованы полностью ( 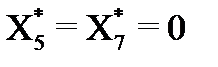), но останется неизрасходованным ресурс 2-го вида в объеме 5 единиц измерения ( ).

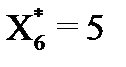3) Составим математическую модель двойственной задачи. Запишем матрицу математической модели исходной задачи.

.

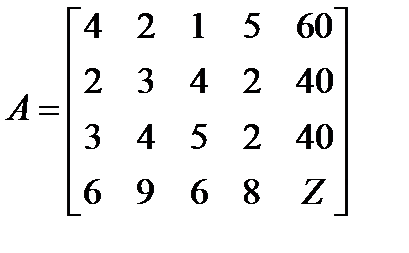Тогда, чтобы получить матрицу математической модели двойственной задачи, необходимо матрицу А транспонировать (т.е. поменять местами соответствующие строки и столбцы).

.

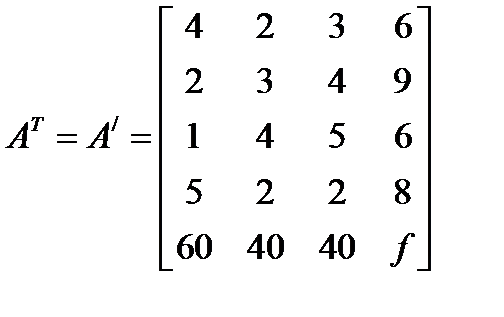Обозначив через 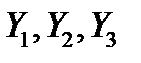– (прикидочные) цены ресурсов, по матрице 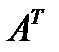строим математическую модель двойственной задачи.

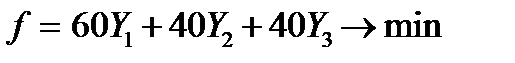(9. 4)

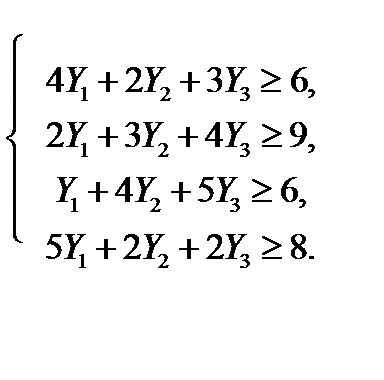(9. 5)

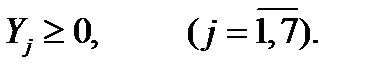(9. 6)

Перейдем к канонической форме записи математической модели двойственной задачи введя дополнительные (балансовые) переменные 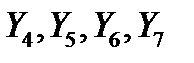, которые означают возможные превышения затрат на производство 1 единицы измерения каждого вида продукции над прибылью, получаемой предприятием.

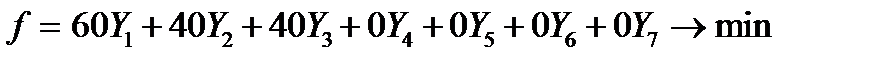(9. 4′)

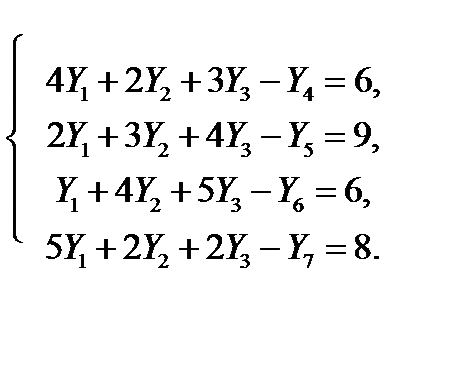(9. 5′)

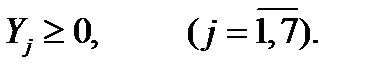(9. 6′)

Из 1-й теоремы двойственности следует, что если решена одна из пары взаимодвойственных задач симплексным методом, то по последней симплексной таблице можем получить и компоненты оптимального плана двойственной задачи (они находятся в индексной строке). При этом необходимо использовать соответствие между переменными пары взаимодвойственных задач:

.

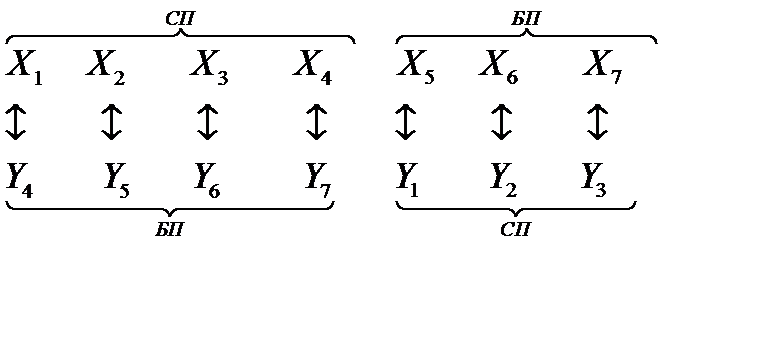Для нашей задачи имеем оптимальный план двойственной задачи:

.

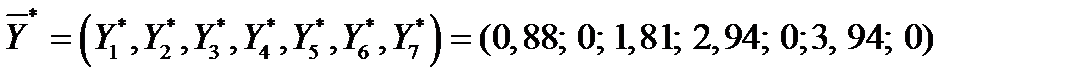4) Оценки для 1-го и 3-го видов ресурсов положительные. Это указывает, что эти виды ресурсов наиболее дефицитные (и используются полностью). Увеличение объема ресурса 1-го вида на одну единицу измерения позволило бы получить увеличение максимальной прибыли предприятия на 0,88 денежных единиц; а для ресурса 3-го вида соответственно на 1,81 денежную единицу. Равенство нулю оценки для ресурса 2-го вида ( 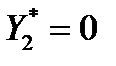) говорит о том, что дальнейшее увеличение объема этого вида ресурса не повлияет на прибыль предприятия (ресурс 2-го вида при оптимальном плане производства остается в избытке).

Дополнительные двойственные переменные являются мерой убыточности продукции, которую согласно оптимальному плану нецелесообразно выпускать. Так как 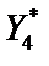= 2,94, то это говорит, что на производстве 1 единицы продукции 1-го вида терпит убытки в количестве 2,94 денежные единицы. Следовательно, при необходимости производства продукции 1-го вида для ее рентабельности необходимо повысить цену на эту продукцию не менее чем на 2,94 денежные единицы.

Так как 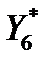=3,94, то это говорит, что на производстве 1-й единицы продукции 3-го вида предприятие терпело убытки в объеме 3,94 денежные единицы (поэтому оно и не планирует эту продукцию производить). При необходимости производство этого вида продукции цена ее реализации должна быть увеличена не менее чем на 3,94 денежные единицы.

Задание 3.

Имеется три поставщика и пять потребителей некоторой продукции. Количество груза 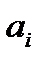, которое может отгрузить поставщик 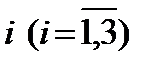, стоимость перевозки из пункта 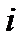в пункт 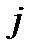единицы груза 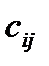и потребности потребителей в грузе 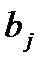, 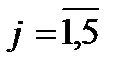заданы матрицей:

= .

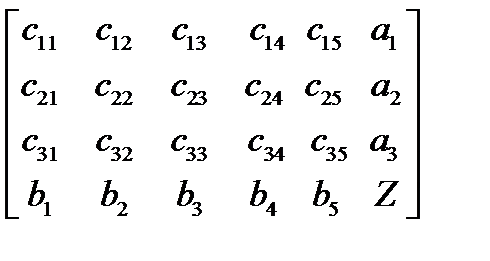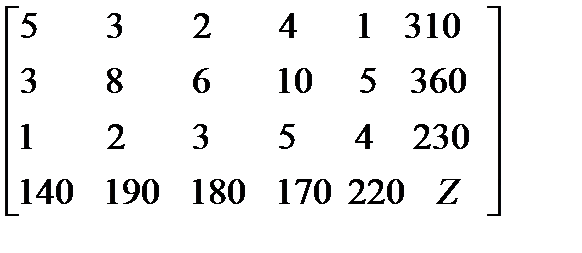Составить экономико-математическую модель задачи и найти методом потенциалов оптимальный план перевозки груза, при котором общие транспортные затраты будут наименьшими.

Решение

Строим математическую модель задачи. Через Х_ij обозначим объем продукции, доставленной от поставщика A_i (i=l,2,3) потребителю B_j ( 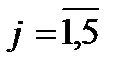). Отметим, что в данном случае сумма количества продукции, которую могут отгрузить все поставщики, совпадает с суммой потребностей потребителей:

310+360+230=140+190+180+170+220 = 900 .

Значит, задача закрытого типа и имеет решение. Математическая модель задачи принимает вид:

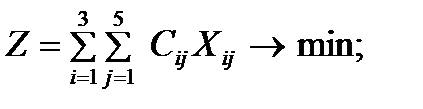(9. 7)

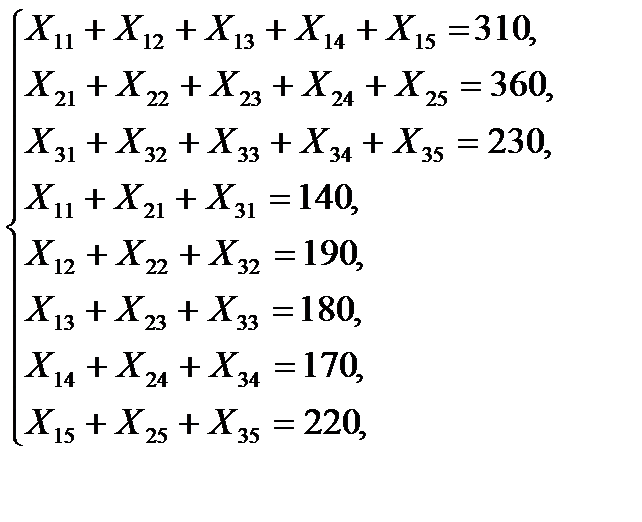(9. 8)

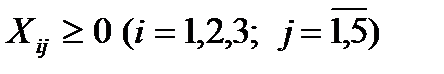. (9. 9)

Строим начальную распределительную таблицу 9. 9:

Таблица 9.9

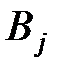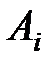	В1	В2	Вз	В4	В5	аi	Ui
А1							-4
А2	+ 3 *	– 8
A3	– 1	+ 2					-6

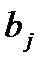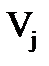Построенному опорному решению отвечают затраты:

Z₁ = 90∙2+220∙1+100∙8+90∙6+170∙10+140∙1+90∙2 = 3760.

Проверим полученный опорный план на оптимальность. Для этого i-й строке и j-му столбцу ставим в соответствие числа U_i и V_j (потенциалы). Для каждой базисной переменной Х_ij потенциалы должны удовлетворять условию

U_i +V_j = С_ij. Получаем систему:

U₁+V₃ = 2, Так как система состоит из 7 уравнений, а неизвестных

U₁+V₅ = l, 8, то, чтобы найти численное решение этой системы, U₂+V₂ = 8, одно из неизвестных зададим произвольно, тогда

U₂+V₃ = 6, остальные переменные найдутся из системы однозначно.

U₂+V₄ = 10,

U₃+V₁ = 1,

U₃+V₂ = 2.

Пусть U₂ = 0, тогда V₂ = 8, V₃ = 6, V₄ = 10, U₁ = − 4, U₃ = −6, V₁ = 7,

V₅ = 5.

Теперь для небазисных переменных (свободных клеток) найдем оценки

Sij = Сij –( Ui +Vj) :
S11 = 5 – (– 4 + 7) = 2	S21 = 3 – ( 0 + 7) = −4
S12 = 3 – (– 4 + 8 ) = – 1	S25 = 5 – (0 + 5) = 0
S14 = 4 – (– 4 + 10) = – 2	S33 = 3 – (– 6 + 6) = 3
S35 = 4 – (– 6 + 5) = 5	S34= 5 – (– 6 + 10) = l

В силу критерия оптимальности опорного плана (все оценки S_ij неотрицательны) делаем вывод, что построенный план не оптимален, т.к. среди оценок есть отрицательные. В базис введем переменную Х₂₁ (отвечающую наибольшей по модулю отрицательной оценке) и строим замкнутый контур с вершинами в загруженных клетках. Присваиваем клеткам в вершинах контура поочередно по часовой стрелке знаки " + " и " – ", начиная с (2,1), которой присваиваем знак " + ". Выбираем наименьшее значение из клеток со знаком

" – " (min (140,100) = 100) и перераспределим продукцию вдоль контура: прибавляя 100 к значениям в клетках со знаком "+" и вычитая из значений в клетках со знаком " – ". В результате приходим к таблице 9.10.

Таблица 9. 10

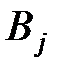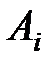	В1	В2	Вз	В4	В5	аi	Ui
А1							−4
А2	+ 3 100			– 10
A3	– 1			+ 5 *			-2

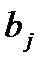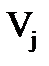Полученному решению отвечают затраты:

Z₂ = 90∙2+220∙1+100∙3+90∙6+170∙10+40∙1+190∙2=3360.

Проверяем полученный план на оптимальность и получаем, что S₃₄ = –3 < 0. Значит, решение неоптимальное и строим в таблице 12 новый цикл пересчета для клетки (3,4). Так как min(170,40)=40=Х₃₁ ,то перераспределяем продукцию вдоль контура, прибавляя 40 к значениям в клетках со знаком " + " и вычитая из значений в клетках со знаком " – ". В результате получаем таблицу 9. 11.

Таблица 9. 11

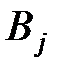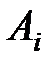	В1	В2	Вз	В4	В5	аi	Ui
А1			– 2 –	+ 4 *			–4
А2			+ 6	– 10
A3							–5

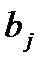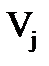Полученному решению отвечают затраты:

Z₃ = 90∙2+220∙l+140∙3+90∙6+130∙10+190∙2+40∙5=3240.

Аналогично предыдущему проверяем полученный план на оптимальность. Получаем, что S₁₄ = – 2 < 0. Теперь для улучшения плана загрузим клетку (1,4). В итоге приходим к таблице 9.12.

Таблица 9.12

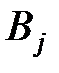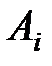	В1	В2	Вз	В4	В5	аi	Ui
А1				+ 4	– 1		–6
А2			б	– 10	+ 5 *
A3							–5

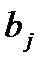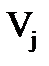Z₄ = 90∙4+220∙l+140∙3+180∙6+40∙10+190∙2+40∙5=3060.

Среди оценок свободных клеток имеем S₂₅ = –2<0, следовательно, полученный план перевозок не является оптимальным, и для его улучшения необходимо загрузить клетку (2,5). В итоге вычислений приходим к таблице 9.13.

Таблица 9.13

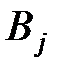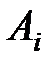	В1	В2	Вз	В4	В5	аi	Ui
А1							–4
А2			б
A3							–3

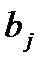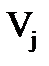Z₅ = 130∙4+180∙l+140∙3+180∙6+40∙5+190∙2+40∙5=2980.

Полученный план оказывается оптимальным, так как все оценки незагруженных клеток неотрицательны. По этому плану перевозок 1–й поставщик отправляет 130 ед. продукции потребителю В₄ и 180 ед. – B₅; 2–й поставщик – 140 ед. потребителю В₁, 180 ед. потребителю B₃ и 40 ед. потребителю В₅; 3–й поставщик – 190 ед. потребителю B₂ и 40 ед. потребителю В₄.

Вопросы для подготовки к экзамену