Этот метод удобен только для плоской системы сил. Если система сил пространственная, то существует аналитический способ.
п 5. Аналитический способ определения равнодействующей системы сходящихся сил .
Вводим координатную систему сначала в точке схода. Оси направляем совершенно произвольно, т.е. так как нам удобно.
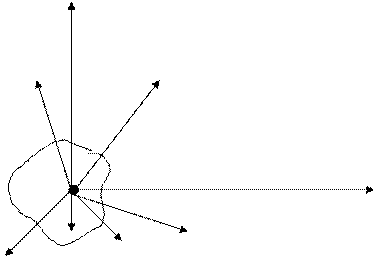 Z
Z
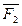
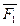
Y
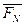
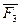

X
Пусть силы системы заданы своими проекциями:
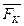 {XK,YK,ZK}
{XK,YK,ZK}
Воспользуемя тем, что равнодействующая системы сходящихся сил равна сумме всех сил
 =
= 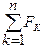 (1)
(1)
Вопрос: Что делать с этим уравнением, чтобы появились проекции сил?
Ответ:
Спроецировать это векторное равенство на оси координат.
Пишем
Спроецируем это равенство на оси координат:
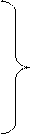 RX =
RX = 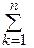 XK
XK
RY = 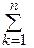 YK (2)
YK (2)
R Z= 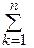 ZK
ZK
Вопрос:
Найдем проекцию равнодействующей через проекции системы сил
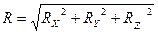 (3)
(3)
Направление определим через направляющие косинусы.
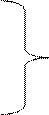 Cos (
Cos (  ,
, 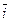 ) =
) = 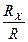
Cos (  ,
, 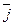 ) =
) = 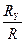 (4)
(4)
Cos (  ,
, 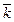 ) =
) = 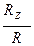
П 6. Условия равновесия системы сходящихся сил.
Теорема:
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая была равна нулю
 =0 (5)
=0 (5)
Сначала докажем необходимость
Вопрос:
Что нам дано? Что нам надо доказать?
Ответ:
Пусть эта система уравновешена, надо доказать, что  =0.
=0.
А достаточность наоборот: пусть  =0, тогда система уравновешена.
=0, тогда система уравновешена.
Вопрос:
Как это делается?
Ответ:
Давайте вспомним аксиому №1,аксиому равновесия.
В ней речь идет о двух силах действующих на тело. Для равновесия такой системы необходимо и достаточно, чтобы у них было:
· общая линия действия
· одинаковые модули
· силы направлены в противоположные стороны.
Если мы сможем эту систему из любого числа сил заменить двумя силами, то можно будет убедиться, что  =0.
=0.
Этого будет необходимо и достаточно .
Дано:
S( 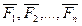 )
) 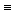 0;
0;
Доказать
 =0
=0
Доказательство:
Заменяем эту систему равнодействующей
S( 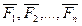 )
) 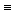
 ;
;
Причем
 =
= 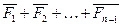
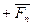
Но можно эту систему заменить двумя силами
S( 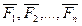 )
) 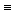 S1(
S1( 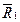 ,
, 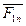 )
)
Где
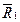 =
= 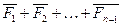
Причем
 =
= 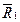 +
+ 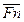 (6)
(6)
По условию S( 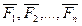 )
) 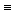 0;
0;
По аксиоме №1
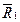 ,
, 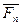 - должны иметь общую линию действия
- должны иметь общую линию действия
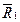 = -
= - 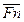
Тогда из (6)
 =0
=0
Что и требовалось доказать.
Из условия (5) можно получить векторное условие равновесия для сил данной системы S( 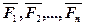 ).
).
Векторное условие
Т.к.
 =
= 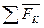 , то
, то
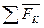 =0 (7)
=0 (7)
Это необходимое и достаточное условие для равновесия такой системы записанное в векторной форме.
Для равновесия такой системы необходимо и достаточно чтобы векторная сумма всех сил такой системы была равна нулю
Геометрическое условие
Вспомним геометрический способ нахождения равнодействующей.
Это построение замыкающей стороны силового многоугольника
Для системы находящейся в равновесии  =0. конец последней силы должен совпадать с началом первой.
=0. конец последней силы должен совпадать с началом первой.
Запишем.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
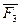
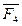
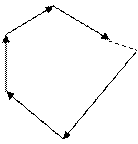
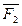
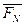
. 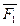
Аналитическое условие равновесия системы сходящихся сил
Из выражения
 =0
=0
Следует, что
RX = 0, RY = 0, R Z= 0
Или на основании (2)
Сумма проекций всех сил на ось Х равно нулю и т. д.
 ∑XK=0
∑XK=0
∑YK=0 (8)
∑ZK=0
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций всех сил системы на каждую из трех координатных осей были равны нулю.
