Реакция такого шарнира, если не учитывать трение, может проходить по любой прямой через центр шарнира А.

Действительное направление реакции шарнира можно определить только при решении задач.

Обычно реакцию раскладывают на три составляющие параллельные координатным осям. Если мы найдем эти составляющие, то мы найдем и реакцию.

Подпятник это тоже шарнир, у которого имеется опорная поверхность. Его реакцию мы тоже раскладываем на составляющие.

Подпятник похож на обычный цилиндр или металлический стакан с опорной площадкой.

В рассмотренных выше примерах связей, трением мы пренебрегали.

Но на практике встречаются случаи, когда трение обязательно присутствует.

Такие типы связей мы будем рассматривать на практике.

Гибкая связь.

(нить, канат, трос, цепь, и т.д.)

Реакция 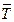гибкой связи направлена вдоль связи от точки прикрепления А к точке подвеса О.

Этот материал выносится на самостоятельное изучение

Литература Прусов В М «Статика»

Стр. 37-36 п. 2.4.7. Невесомый стержень шарнирно закрепленный по концам.

Стр. 39 –43 П2.5 Шероховатая опорная поверхность.

Мы рассмотрели не все типы связей, но самые распространенные.

Поскольку мы будем заменять несвободное тело свободным, для этого мысленно все связи будем отбрасывать и их действие заменять соответствующими реакциями.

Поэтому надо научиться, правильно изображать эти реакции и тогда мы сможем составлять условия равновесия. И самое главное научиться определять эти реакции.

Как это делается, мы увидим на практике.

п 3. Понятие о системе сходящихся сил

· Во – первых, надо установить какой простейший вид эта система сил имеет, чем ее можно заменить.

· Во – вторых, каковы условия равновесия? Каким условиям должны подчиняться силы такой системы, чтобы система, и тем самым и само тело, на которое действует система сил, находилось в равновесии?

Запишем определение:

Системой сходящихся сил называется такая система сил, в которой линии действия всех сил пересекаются в одной точке.

Эта точка О называется точкой схода сил.

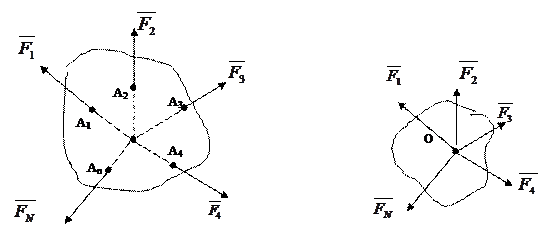Изобразим тело и приложим к нему некоторую систему сил S( )

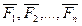Переносим силу 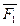в точку О на основании следствия о переносе силы вдоль линии действия, силу 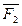в точку 0 и т.д.

S( 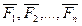) 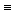S_О( )

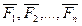Что же получается? Система S( 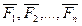) находящаяся слева и система S_О( 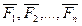) находящиеся справа эквивалентны.

Если силы не лежат в одной плоскости то система называется пространственной, а если все силы лежат в одной плоскости то система называется плоской системой сходящихся сил.

п 4. Геометрический способ определения равнодействующей системы сходящихся сил .

Судя по формулировке понятно, что такую систему можно заменить одной силой.

Теорема: Система сходящихся сил эквивалентна одной силе, т.е. имеет равнодействующую, равную геометрической сумме сил этой системы.

Т.е.

S( )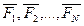

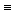
Вопрос:

Как будем доказывать? У нас есть аксиомы статики, с помощью которых мы можем доказать эту теорему. Какая из аксиом нам нужна?

Ответ:

Аксиома №3 Аксиома параллелограмма сил.

Вопрос:

О чем она говорит?

Ответ:

О том, что две силы, приложенные в одной точке можно заменить одной силой по правилу параллелограмма.

Применяем аксиому № 3

Док-во: Сначала складываем по правилу параллелограмма первую и вторую силы, равнодействующую двух сил складываем с третей силой и т.д. Все силы переберем и получим одну силу , которая будет выражаться как векторная сумма. Вместо параллелограмма сил можно построить треугольники. К первой силе приложить второй вектор и соединить начало и конец и т.д.

= =

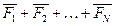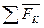
Строить параллелограммы и треугольники дело не слишком приятное. Если много сил, то необходимо строить много треугольников или параллелограммов.

Вопросы:

Как можно этот процесс ускорить? Как можно построить сумму нескольких векторов? Как будет называться фигура построения?

Ответ:

Получится многоугольник из сил системы, а замыкающая сторона будет изображать сумму.

Запишем.

Вместо построения параллелограммов для построения можно построить силовой многоугольник. Он строиться в стороне в выбранном масштабе

.

.

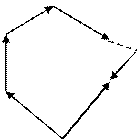
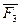
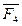
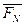
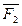
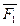
Вопрос:

Всегда ли удобно строить многоугольники?