Парная линейная регрессия. Взаимосвязи экономических переменных.

Парная линейная регрессия. Взаимосвязи экономических переменных.

В модели парной линейной регрессии одна из величин Х выделяется как независимая (объясняющая), а другая Y как зависимая (объясняемая). Например, рост дохода ведет к увеличению потребления; рост цены ведет к снижению спроса; снижение процентной ставки ведет к увеличению инвестиций.

Независимая переменная Х называется также входной, экзогенной, предикторной (предсказывающей), фактором, регрессом, факторной переменной.

Зависимая переменная Y называется также выходной, результирующей, эндогенной, результативным признаком, функцией отклика.

Определение: Зависимость среднего значения переменной Y, т.е. условного математического ожидания Y при данном значении Х = х

𝑀 (𝑌/𝑋 = 𝑥) = 𝑓(𝑥),

называется функцией парной регрессии Y на Х.

Реальные значения Y могут быть различными при одном и том же значении Х = х, поэтому фактическая зависимость имеет вид:

Y = M(Y│x) +ε,

где величина ε называется случайным отклонением.

Суть регрессионного анализа.

Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.

Уравнение регрессии или модель связи социально-экономических явлений выражается функцией. Различают парную (y=f(x)) и множественную (Ŷ=f( 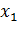, ,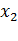… 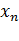) ) регрессии.

Парная регрессий описывает связь между двумя признаками (результативным и факторным). Множественная регрессия описывает связь между результативным признаком и двумя и более факторными признаками.

Классическая линейная регрессионная модель.

Если функция регрессии линейна: M(Y│x) = 𝛽0 + 𝛽1𝑥, то регрессия называется линейной.

Теоретическая модель парной линейной регрессии (зависимость между переменными в генеральной совокупности) имеет вид: 𝑌 = 𝛽0 + 𝛽1𝑋 + 𝜀, где Х рассматривается как неслучайная переменная, а Y и ε как случайные величины; 𝛽0 и 𝛽1 - теоретические коэффициенты (параметры) регрессии.

Индивидуальные значения yi выражаются: yi = 𝑏0 + 𝑏1 xi + ε. Для определения 𝛽0 и β необходимо знать и использовать все значения переменных Х и Y генеральной совокупности, что практически невозможно. Методами регрессионного анализа возможно лишь получить их оценки на основании выборочных данных: b0 𝛽0 b1 𝛽1

Предпосылки МНК

1) Математическое ожидание случайных отклонений 𝜀𝑖 равно нулю: 𝑀 𝜀𝑖 = 0 для всех наблюдений. Это означает, что случайное отклонение не должно иметь систематического смещения.

2) Дисперсия случайных отклонений постоянна для всех наблюдений: 𝐷 𝜀𝑖 = 𝑀 𝜀𝑖 2 = 𝜎 2 , 𝑖 = 1, 2, … , 𝑛. Выполнимость данной предпосылки называется гомоскедастичностью, а невыполнимость ее называется гетероскедастичнстью.

3) Случайные отклонения 𝜀𝑖 и 𝜀𝑗 ( i ≠ j ) не коррелируют (отсутствует автокорреляция ): 𝑀 𝜀𝑖 , 𝜀𝑗 = 0, 𝑖 ≠ 𝑗 . 4 3) Случайные отклонения должны быть статистически независимы (некоррелированы) от объясняющих переменных.

4) Отсутствие мультиколлинеарности. Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.

5) Отклонения 𝜀𝑖 , 𝑖 = 1, 2, … , 𝑛 имеют нормальные распределения 𝜀𝑖 ≅ 𝑁(0; 𝜎 2 )Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

Замечание: При построении классических линейных регрессионных моделей считается также, что объясняющие переменные не являются случайными величинами.

14.Множественная линейная модель. Проблема мультиколлинеарности.

Мультиколлинеарностью называется высокая степень коррелированности двух или нескольких объясняющих переменных в уравнении множественной регрессии. Крайним случаем мультиколлинеарности является линейная зависимость между объясняющими переменными. Считается, что две переменные 𝑋𝑖 и 𝑋𝑗 сильно коррелированны, если выборочный коэффициент корреляции двух объясняющих переменных 𝑟𝑥𝑖 𝑥𝑗 > 0,7

Поясним. Пусть имеется m объясняющих факторов:𝑋1 , 𝑋2 , … . , 𝑋𝑚 . Матрица межфакторной корреляции состоит из парных коэффициентов корреляции и имеет вид:

Наличие мультиколлинеарности можно подтвердить, найдя определитель матрицы межфакторной корреляции. Если 𝑅𝑥𝑥 ≈ 1, то мультиколлинеарность отсутствует, а если 𝑅𝑥𝑥 ≈ 0, то - присутствует. Совершенная мультиколлинеарность является скорее в теории, а практически между некоторыми объясняющими переменными существует очень сильная коореляционная зависимость 𝑟𝑥𝑖 𝑥𝑗 > 0,7, а не функциональная 𝑟𝑥𝑖 𝑥𝑗 = 1.

Последствия мультиколлинеарности:

1. Большие дисперсии (стандартные ошибки) оценок коэффициентов уравнения множественной регрессии. Это расширяет интервальные оценки, ухудшая их точность. Последнее затрудняет нахождение истинных значений оценок коэффициентов.

2. Уменьшаются t-статистики оценок. Оценки имеют малую статистическую значимость, в то время как модель в целом является значимой (имеет высокое значение коэффициент детерминации 𝑅^2).

3. Оценки коэффициентов уравнения по МНК и их стандартные ошибки становятся очень чувствительными к малейшим изменениям данных. Оценки коэффициентов становятся неустойчивыми.

4. Затрудняется определение доли вклада каждой из объясняющих переменных в объясняемую уравнением регрессии дисперсию зависимой переменной.

5. Возможно получение неверного знака у коэффициента регрессии.

15. Множественная линейная модель. Методы определения мультиколлинеарности.

Уравнение линейной множественной регрессии имеет вид 𝑦 = 𝑏0 + 𝑏1 𝑥1 + 𝑏n 𝑥n

Существует несколько признаков, по которым может быть установлено наличие мультиколлинеарности.

1. Коэффициент детерминации R^2 достаточно высок, но некоторые из коэффициентов уравнения множественной линейной регрессии статистически незначимы (имеют низкие t-статистики).

2. Высокая корреляция в уравнении регрессии с двумя объясняющими переменными. Если объясняющих переменных больше двух целесообразнее использовать частные коэффициенты корреляции.

Частным коэффициентом корреляции называется коэффициент корреляции между двумя объясняющими переменными, очищенный от влияния других переменных. Например, при трех объясняющих переменных Х1, Х2, Х3 частный коэффициент корреляции между Х1 и Х3, очищенный от Х2, рассчитывается по формуле:

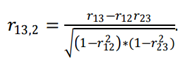
Замечание: частный коэффициент корреляции может существенно отличаться от «обычного» коэффициента корреляции. Для более обоснованного вывода о корреляции между парами объясняющих переменных необходимо рассчитывать все частные коэффициенты корреляции.

Парные коэффициенты корреляции, рассчитанные по формуле:

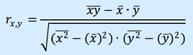
3. Сильная регрессия между объясняющими переменными. Какая- либо из объясняющих переменных является комбинацией других объясняющих переменных (линейной или близкой к линейной).

16. Множественная линейная модель. Методы уменьшения мультиколлинеарности.

Мультиколлинеарность является серьезной проблемой если целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую переменную. Наличие мультиколлинеарности, приводит к увеличению стандартных ошибок, искажая истинные зависимости между переменными. При прогнозировании будущих значений зависимой переменной при высоком коэффициенте детерминации (R 2 >0,9) наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели.

Единого метода устранения мультиколлинеарности не существует. Это связано с тем, что причины и последствия мультиколлинеарности неоднозначны и во многом зависят от результатов выборки. Перечислим наиболее употребительные методы.

1) Исключение переменной из модели. Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных. Однако необходима определенная осмотрительность при применении данного метода. В этой ситуации возможны ошибки спецификации. В эконометрических моделях, применяемых в прикладных целях, желательно не исключать объясняющую переменную до тех пор, пока мультиколлинеарность не станет серьезной проблемой.

2) Получение дополнительных данных или новой выборки. Возможно, для уменьшения мультиколлинеарности достаточно увеличить объем выборки. Это сократит дисперсии коэффициентов регрессии и тем самым увеличит их статистическую значимость.

3) Изменение спецификации модели. Иногда проблема мультиколлинеарности может быть решена путем изменения спецификации модели.

4) Использование предварительной информации о некоторых параметрах. Возможно, что значения коэффициентов, рассчитанные для каких- либо предварительных моделей, или для аналогичной модели по ранее полученной выборке, могут быть использованы для исследуемой в данный момент модели.

5) Преобразование переменных. Иногда минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных: разделив все переменные уравнения множественной регрессии на одну из коррелирующих переменных.

17. Нелинейная регрессия. Виды моделей. Примеры.

Нелинейная регрессия – моделирование экономических зависимостей линейными уравнениями во многих практических случаях дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Из-за многообразия и сложности экономических процессов ограничиться рассмотрением одних лишь линейных регрессионных моделей невозможно. Большинство экономических процессов и, следовательно, отражающих их экономических зависимостей, не являются линейными по своей сути. Моделирование таких процессов линейными уравнениями регрессии не дает положительного результата.

Например, при рассмотрении производственных функций линейная модель не является реалистичной. Обычно при моделировании таких процессов используются степенные модели. Наиболее широкую известность имеет производственная функция Кобба-Дугласа

𝑌 = 𝐴 ∙ 𝐾𝛼∙ 𝐿𝛽
(здесь 𝑌 — объем выпуска; К и L — затраты капитала и труда

соответственно; А, 𝛼 и 𝛽 — параметры модели).
В современном эконометрическом анализе применяются и многие

другие нелинейные модели.

Построение и анализ нелинейных моделей имеют свою специфику. Мы ограничимся рассмотрением нелинейных моделей, допускающих сведение их к линейным. Это так называемые линейные относительно параметров модели. Далее будут рассмотрены модели парной регрессии в силу их простоты, а также примеры применения нелинейных уравнений с несколькими объясняющими переменными.

Виды моделей:

1. Логарифмические модели

2. Полулогарифмические модели

3. Лог-линейная модель

4. Линейно-логарифмическая модель

5. Обратная модель

6. Степенная модель

7. Показательная модель

18. Нелинейная регрессия. Выбор формы модели.

Нелинейная регрессия – моделирование экономических зависимостей линейными уравнениями во многих практических случаях дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Из-за многообразия и сложности экономических процессов ограничиться рассмотрением одних лишь линейных регрессионных моделей невозможно. Большинство экономических процессов и, следовательно, отражающих их экономических зависимостей, не являются линейными по своей сути. Моделирование таких процессов линейными уравнениями регрессии не дает положительного результата.

Выбор формы модели:

Многообразие и сложность экономических процессов предопределяет многообразие моделей, используемых для эконометрического анализа. С другой стороны, это существенно усложняет процесс нахождения максимально адекватной формулы зависимости. Для случая парной регрессии подбор модели обычно осуществляется по виду расположения наблюдаемых точек на корреляционном поле. Однако нередки ситуации, когда расположение точек приблизительно соответствует нескольким функциям и необходимо из них выявить наилучшую. Например, криволинейные зависимости могут аппроксимироваться полиномиальной, показательной, степенной, логарифмической функциями. Еще более неоднозначна ситуация для множественной регрессии, так как наглядное представление статистических данных в этом случае невозможно.

Правильный выбор вида экономической модели является отправной точкой для качественного ее анализа. На практике неизвестно, какая модель является верной, и зачастую подбирают такую модель, которая наиболее точно соответствует реальным данным. Поэтому, чтобы выбрать качественную модель, необходимо ответить на ряд вопросов, возникающих при ее анализе:

1. Каковы признаки «хорошей» (качественной) модели?

2. Какие ошибки спецификации встречаются, и каковы последствия данных ошибок?

3. Как обнаружить ошибку спецификации?

4. Каким образом можно исправить ошибку спецификации и перейти к лучшей (качественной) модели?

19. Нелинейная регрессия. Проблемы спецификации.

Нелинейная регрессия – моделирование экономических зависимостей линейными уравнениями во многих практических случаях дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Из-за многообразия и сложности экономических процессов ограничиться рассмотрением одних лишь линейных регрессионных моделей невозможно. Большинство экономических процессов и, следовательно, отражающих их экономических зависимостей, не являются линейными по своей сути. Моделирование таких процессов линейными уравнениями регрессии не дает положительного результата.

Проблемы спецификации:

Стандартная схема анализа функциональных зависимостей состоит в осуществлении ряда последовательных процедур.

 Подбор начальной модели. Он осуществляется на основе экономической теории, предыдущих знаний об объекте исследования, опыта исследователя и его интуиции. 


 Оценка параметров модели на основе имеющихся статистических данных. 


 Осуществление тестов проверки качества модели (обычно используются t-статистики для коэффициентов регрессии, F- статистика для коэффициента детерминации, статистика Дарвина- Уотсона для анализа отклонений и ряд других тестов). 


 При наличии хотя бы одного неудовлетворительного ответа по какому-либо тесту модель совершенствуется с целью устранения выявленного недостатка. 


 При положительных ответах по всем проведенным тестам модель считается качественной. Она используется для анализа и прогноза объясняемой переменной. 


Несколько важных замечаний.

1. Необходимо предостеречь от абсолютизации полученного результата, поскольку даже качественная модель является подгонкой спецификации модели под имеющийся набор данных. Реальна картина, когда исследователи, обладающие разными наборами данных, строят разные модели для объяснения одной и той же переменной.

2. Проблематичным является и использование модели для прогнозирования значений объясняемой переменной. Иногда хорошие с точки зрения диагностических тестов модели обладают весьма низкими прогнозными качествами.

3. Достаточно спорным является вопрос, как строить модели:
а) начинать с самой простой и постоянно усложнять ее;
б) начинать с максимально сложной модели и упрощать ее на основе

проводимых исследований.
Оба подхода имеют как достоинства, так и недостатки. Например, если следовать схеме а), то происходит обыкновенная подгонка модели под эмпирические данные. При теоретически более оправданном подходе б) поиск возможных направлений совершенствования модели зачастую сводится к полному перебору, что делает проводимый анализ неэффективным. На этапах упрощения модели возможно также отбрасыва- ние объясняющих переменных, которые были бы весьма полезны в упрощенной модели.

Вывод: построение модели является индивидуальным в каждой конкретной ситуации и опирается на серьезные знания экономической теории и статистического анализа.

20. Суть гетероскедастичности.

Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений: дисперсия случайных отклонений 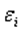постоянна. 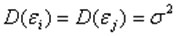для любых наблюдений i иj.

Выполнимость данной предпосылки называется гомоскедастичностъю (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностъю (непостоянством дисперсий отклонений).

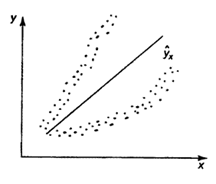
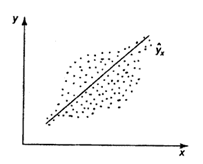
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 1).

А б

в

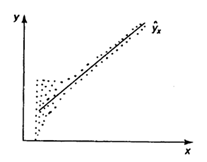
Рис. 1 Примеры гетероскедастичности.

На рис. 1 изображено: а – дисперсия остатков растет по мере увеличения 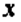; б – дисперсия остатков достигает максимальной величины при средних значениях переменной и уменьшается при минимальных и максимальных значениях ; в – максимальная дисперсия остатков при малых значениях и дисперсия остатков однородна по мере увеличения значений .

21. Последствия гетероскедастичности.

Последствия гетероскедастичности:

– Оценки коэффициентов по-прежнему останутся несмещёнными и линейными.

– Оценки не будут эффективными (т. е, они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра), Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.

– Дисперсии оценок будут рассчитываться со смещением.

Поэтому выводы, получаемые на основе соответствующих t- и F- статистик, а также интервальные оценки коэффициентов регрессии будут ненадежными. Следовательно, статистические выводы, могут быть ошибочными и приводить к неверным заключениям по построенной модели.

22. Обнаружение гетероскедастичности.

Обнаружение гетероскедастичности в каждом конкретном случае является сложной задачей. Для знания дисперсий отклонений необходимо знать распределение случайной величины Y, соответствующее выбранному значению 𝑥𝑖. Практически, для каждого конкретного значения 𝑥𝑖определяется единственное значение 𝑦𝑖, что не позволяет оценить дисперсию случайной величины Y. Поэтому, не существует какого-либо однозначного метода определения гетероскедастичности.

Наиболее популярным является тест Голдфелда-Квандта.

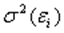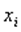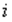Данный тест используется для проверки следующего типа гетероскедастичности: когда среднее квадратическое отклонение случайной составляющей пропорционально значению признака-фактора в -м наблюдении. При этом делается предположение, что случайная составляющая распределена нормально.

Алгоритм-тест Голдфелда-Квандта приведен ниже.

Все наблюдения 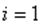; 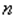упорядочиваются по значению .

Оценивается регрессия: 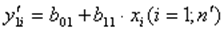для первых 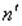наблюдений.

Оценивается регрессия: 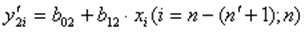для последних наблюдений .

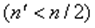Рассчитывают суммы квадратов отклонений фактических значений признака-результата от его расчетных значений для обеих регресси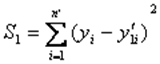й:

и .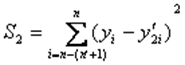

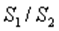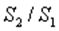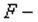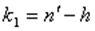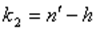Находят отношение сумм квадратов отклонений: (или ). В числителе должна быть наибольшая из сумм квадратов отклонений. Данное отношение имеет распределение со степенями свободы: и , где 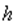- число оцениваемых параметров в уравнении регрессии.

Если 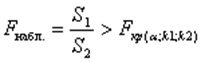, то гетероскедастичность имеет место.

Если в модели более одного фактора, то наблюдения должны упорядочиваться по тому фактору, который, как предполагается, теснее связан с , и должно быть больше, чем .

23. Методы смягчения проблемы гетероскедастичности.

При наличии гетероскедастичности 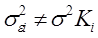и величина Ki может меняться от одного значения фактора к другому. При наличии гетороскедастичности вместо обычного МНК используют обобщенный МНК (взвешенный). Суть метода заключается в уменьшении вклада данных наблюдений, имеющих большую дисперсию в результате расчета.

1 случай. Если дисперсии возмущений известны 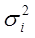, то гетероскедастичность легко устраняется. Вводят новые переменные: 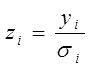; ; 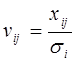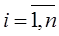, 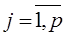. Регрессионная модель в векторной форме

(*) /:

, .

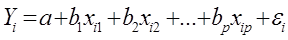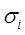
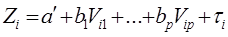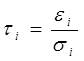При этом 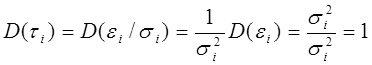, т.е. модель гомоскедастична.

2 случай. Если дисперсии возмущений неизвестны, то делают реалистические предположения о значениях .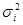

Например:

а) дисперсии 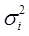пропорциональны xi: 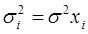. Уравнение регрессии (*) делят

- на 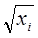- в случае одной переменной; - на 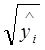- в случае множественной регрессии.

б) дисперсии 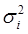пропорциональны 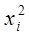, т.е.

,

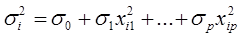Уравнение регрессии (*) делят на хi.

24. Временные ряды. Основные составляющие временного ряда.

Временной ряд– это набор чисел, привязанный к последовательным, обычно равноотстоящим моментам времени. Числа, составляющие временной ряд и получающиеся в результате наблюдения за ходом некоторого процесса, называютсяуровнямивременного ряда илиэлементами.Под длиной временного ряда понимают количество входящих в него уровнейn. Временной ряд обычно обозначаютY(t), или Y_t, гдеt=1,2,…,n.

В общем случае каждый уровень временного можно представить как функцию четырех компонент: f(t), S(t), U(t), E(t) , отражающих закономерность и случайность развития.

Где f(t) – тренд (долговременная тенденция) развития;S(t) – сезонная компонента;U(t) –циклическая компонента; E(t)– остаточная компонента.

В модели временного ряда принято выделять две основные составляющие: детерминированную (систематическую) и случайную. Под детерминированной составляющей временного ряда y₁,y₂ …y_n понимают числовую последовательность, элементы которой вычисляются по определенному правилу как функция времениt. Исключив детерминированную составляющую из данных, мы получим колеблющийся вокруг нуля ряд, который может в одном предельном случае представлять случайные скачки, а в другом – плавное колебательное движение.

В анализе случайного компонента экономических временных рядов важную роль играет сравнение случайной величины E_t c хорошо изученной формой случайных процессов - стационарными случайными процессами.

Стационарным процессомв узком смысле называется такой слу­чайный процесс, вероятностные свойства которого с течением вре­мени не изменяются. Он протекает в приблизительно одно­родных условиях и имеет вид непрерывных случайных колебаний вокруг некоторого среднего значения. Причем ни средняя ампли­туда, ни его частота не обнаруживают с течением времени суще­ственных изменений.

Однако на практике чаще встречаются процессы, вероятностные характеристики которых подчиняются определенным закономерно­стям и не являются постоянными величинами. Поэтому в прикладном эконометрическом анализе используется понятие слабой стационарности (или стационарности в широком смысле), которое предполагает неизменность во времени среднего значения, дисперсии и ковариации временного ряда. Случайный процесс называется стационарным в широком смысле, если его математическое ожидание постоянно и авто­корреляционная функция r(t) зависит только от длины временного интервала t.

В зависимости от вида связи между этими компонентами может быть построена либо аддитивная модель:

Y(t) =f(t)+ S(t)+U(t)+E(t);

либо мультипликативная модель:

Y(t) =f(t) S(t) U(t)+e(t)

временного ряда.

В процессе формирования значений временных рядов не всегда участвуют все четыре компоненты. Однако во всех случаях предполагается наличие случайной составляющей.

Основная цель статистического анализа временных рядов – изучение соотношения между закономерностью и случайностью в формировании значений уровней ряда, оценка количественной меры их влияния. Закономерности, объясняющие динамику показателя в прошлом, используются для прогнозирования его значений в будущем, а учет случайности позволяет определить вероятность отклонения от закономерного развития и его возможную величину.

Последствия автокорреляции.

Последствия автокорреляции в определенной степени сходны с последствиями гетероскедастичности. Среди них при применении МНК выделяют следующие. 1. Оценки параметров, оставаясь несмещенными и линейными, перестают быть эффективными. Поэтому, они перестают обладать свойствами наилучших линейных несмещенных оценок. 2. Дисперсии оценок коэффициентов являются смещенными. Дисперсии часто, являются заниженными, что влечет за собой увеличение t-статистик. 3. Оценка дисперсии регрессии S2 является смещенной оценкой истинного значения σ2, во многих случаях занижая его. 4. Выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии уравнения и коэффициента детерминации R2, возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

Обнаружение автокорреляции.

Автокорреляция — корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько периодов времени назад. Автокорреляция случайной составляющей ε — корреляционная зависимость текущих 𝜀𝑖 и предыдущих и 𝜀𝑖−𝐿 значений случайной составляющей. Величина L называется запаздыванием, сдвигом во времени или лагом. Лаг определяет порядок автокорреляции. Автокорреляция случайной составляющей нарушает 3-ю предпосылку нормальной линейной модели регрессии: случайные отклонения 𝜀𝑖 и 𝜀𝑗 (i ≠ j) не коррелируют (отсутствует автокорреляция): 𝑀 𝜀𝑖 , 𝜀𝑗 = 0, 𝑖 ≠ 𝑗 .Обычно автокорреляция встречается при использовании данных временных рядов. Допустим, что случайная составляющая обусловлена только невключением в модель объясняющих переменных. Тогда, если значение 𝜀𝑖 в i-м наблюдении должно быть независимым от его значения в предыдущем (i - L)-oм наблюдении 𝜀𝑖−𝐿 , то и значение любой факторной переменной, «скрытой» в ε, должно быть некоррелированным с ее значением в предыдущем наблюдении. Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных. Автокорреляция может быть как положительной, так и отрицательной. Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результат. Отрицательная автокорреляция означает разнонаправленное действие неучтенных в модели факторов на результат, что приводит к отрицательной корреляции между последовательными значениями случайной составляющей. Выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии уравнения и коэффициента детерминации R 2 , возможно, будут неверными. Вследствие этого ухудшаются прогнозные качества модели.

Фиктивные переменные сдвига. Пример.

Фиктивная переменная – это качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков, принимающих два значения, но и несколько возможных. В этом случае добавляются несколько фиктивных переменных.

Фиктивная переменная сдвига – это фиктивная переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной.

К примеру, если рассматривается модель затрат на обучение в зависимости от количества учащихся и типа школы: общеобразовательной и специализированной.

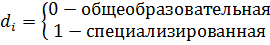
В таком случае спецификационную модель можно записать как: y_i=b₀+b₁x_i+b₂d_i+e_i, где x – непрерывная переменная (количество учащихся), а d – фиктивная (тип школы). В таком случае у нас получится уравнение регрессии, из которого получается две отдельные модели (путем присвоения переменной d значений 1 и 0):

y_i=b₀+b₁x_i+e_i – для обычных школ

y_i=(b₀+b₂)+b₁x_i+e_i – для специализированных школ.

Таким образом, в зависимости от типа школы график моделей сместиться вверх или вниз относительно оси ординат.

Фиктивные переменные наклона. Пример.

Фиктивная переменная – это качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. При этом фиктивные переменные позволяют учесть влияние не только качественных признаков, принимающих два значения, но и несколько возможных. В этом случае добавляются несколько фиктивных переменных.

Фиктивная переменная наклона – это фиктивная переменная, которая изменяет наклон линии регрессии в случае использования качественной переменной. Фиктивные переменные сдвига оказываются полезными при моделировании процессов, в которых при достижении некоторого определенного значения количественной переменной (например, времени) изменяется угол наклона прямой.

К примеру, приобретение дополнительного электроприбора изменяет интенсивность потребления электроэнергии, но не скачкообразно, а непрерыво. Предположим, что электроприбор был приобретен в третий год измерений, тогда необходимо ввести фиктивную переменную d и перекрестную (фиктивную наклона) q=d*t.

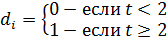
Тогда спецификационную модель можно записать в виде: y_i=b₀+b₁t_i+b₂d_i+b₃q+e_i. Соответственно, график такой модели будет выглядеть следующим образом: дорисовать график, где прямая от 0 до 2 идет под углом вверх, а с 2 и дальше под более крутым углом вверх.

Фиктивные переменные наклона в уравнении регрессии. Пример

Любые примеры обеспечивали интерпретацию сдвига графиков (вверх, вниз) при изменении качественного признака. При этом предполагалось, что наклон графика не зависит от качественного признака, что не всегда верно. В связи с этим введем фиктивную переменную для коэффициента наклона, называемый иногда фиктивной переменной взаимодействия. В любом ранее примере с рождением первенца/не первенца уравнение регрессии имело вид: D=0- если первенец; D=1-если не первенец

Введем дополнительную фиктивную переменную для коэффициента наклона графика:

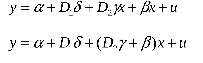
D1=0,D2=0, если первенец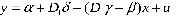

D1=0,D2=0, если первенец

D1=1,D2=1, если не первенец

Доугерти провел исслед-ие и получил: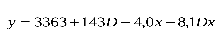

Если первенец=(3363-4х)гр. Если матери курят, (график)

Если не перв.=(3410-12х)гр. то вес меньше

58. Какие существуют способы построения систем линейных одновременных уровнений? Чем они отличаются друг от друга?

Наибольшее распространение в эконометрических исследованиях получила система одновременных (взаимозависимых) уравнений. В ней одни и те же зависимые (исследуемые) переменные в одних уравнениях входят в левую часть, а других – в правую часть системы. Даже в простейшем случае системы одновременных линейных уравнений (eё также называют структурной формой модели – СФМ) :

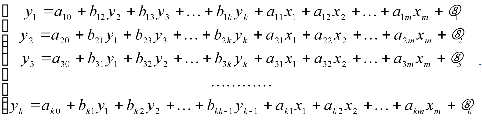
определение параметров модели сталкивается с большими трудностями и не всегда возможно в принципе. Для нахождения параметров модели исходная система одновременных линейных уравнений сводится к приведённой форме модели (ПФМ), которая имеет вид системы независимых переменных:

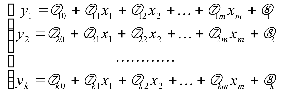
Такое сведение всегда возможно произвести с помощью алгебраических преобразований исходной системы уравнений. Параметры приведённой системы δij можно находить с помощью МНК. Основная трудность заключается в том, что не всегда возможно по коэффициентам приведённой системы восстановить коэффициенты исходной системы уравнений, то есть осуществить обратный переход (подобно тому, как мы это делали, сводя нелинейное уравнение к линейному, находя параметры линейной модели, а затем производя обратный пересчёт параметров нелинейной модели).

Проблема перехода от приведённой формы (ПФМ) системы уравнений к исходной СФМ называется проблемой идентификации. Различаются идентифицируемые, неидентифицируемые и сверхидентифицируемые модели.

Модель идентифицируема, если все коэффициенты исходной модели определяю