Система взаимозависимых эконометрических моделей. Свойства моделей и их влияние на их качество оценок параметров. Структурная и приведенная формы системы моделей.

Взаимозависимые системы наиболее полно описывают экономическую систему, содержащую, как правило, множество взаимосвязанных эндогенных и экзогенных переменных. Такие модели задаются системой взаимозависимых уравнений следующего вида (п - число эндогенных переменных, т - число экзогенных переменных):

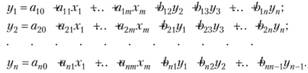
Для нахождения параметров системы взаимозависимых уравнений используются более сложные методы: двух- и трехшаговый метод наименьших квадратов, методы максимального правдоподобия с полной и неполной информацией и др.

На практике стремятся упростить взаимозависимые системы и привести их к так называемому рекурсивному виду. Для этого сначала выбирают эндогенную переменную (внутренний показатель), зависящую только от экзогенных переменных (внешних факторов), обозначают ее у1. Затем выбирается внутренний показатель, который зависит только от внешних факторов и от у1 и т.д.; таким образом, каждый последующий показатель зависит только от внешних факторов и от внутренних предыдущих. Такие системы называются рекурсивными. Параметры первого уравнения рекурсивных систем находят методом наименьших квадратов, их подставляют во второе уравнение, и опять применяется метод наименьших квадратов, и т.д.

Общая задача оценивания заключается в получении каких-либо выводов о параметре У, на основании наблюдений Х1, Х 2,…,. Х n

Существуют следующие критерии оценок параметров:

· несмещенность,

· состоятельность

· эффективность.

Несмещенность оценки означает, что при ее использовании мы не получаем систематической ошибки, и только при наличии этого свойства оценки могут иметь практическую значимость. Математически несмещенность оценки означает, что математическое ожидание остатков равно 0 или E(y)=y .

Следовательно, при большом числе выборочных оцениваний остатки не будут накапливаться и найденный параметр можно рассматривать как среднее значение из возможно большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

Состоятельность оценки гарантирует приближение оценки к истинному значению (т.е. увеличение их точности) при увеличении объема выборки, т.е. должно выполняться равенство

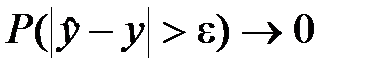
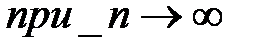
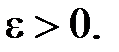
Состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объеме выборки вне зависимости от значений входящих в нее конкретных наблюдений. Состоятельность обычно рассматривается как самое важное свойство оценки (это минимальное требование, предъявляемое к любой оценке).

Признаком несостоятельности оценки является резкое изменение коэффициентов регрессии при изменении объема выборки.

Эффективная оценка является наилучшей в смысле минимума среднеквадратичного отклонения. Оценки, полученные методом наименьших квадратов при выполнении всех необходимых предпосылок (гипотез), являются эффективными.

Несмещенность и эффективность - это свойства, не зависящие от объема выборки n, в то время как состоятельность является асимптотическим свойством при стремлении n к бесконечности.

Для определения качества оценок, полученных методом наименьших квадратов (МНК), необходимо учитывать статистические свойства имеющихся данных.

ei — ошибка (случайные величины).

yi —объясняемая (зависимая) переменная

xi — объясняющая (независимая) переменная или регрессор.

Можно считать, что ei — случайная величина с некоторой функцией распределения, которой соответствует функция распределения случайной величины yi .

Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзоген­ные переменные.

Эндогенные переменные обозначены в приведенной ранее системе одновременных уравнений как у. Это зависимые пере­менные, число которых равно числу уравнений в системе.

Экзогенные переменные обозначаются обычно как х. Это пре­допределенные переменные, влияющие на эндогенные перемен­ные, но не зависящие от них.

Простейшая структурная форма модели имеет вид:

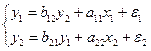
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эн­догенные, а в других — как экзогенные переменные. Внеэкономические переменные (например, климатические условия) вхо­дят в систему как экзогенные переменные. В качестве экзоген­ных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые пере­менные). Так, потребление текущего года (уt) может зависеть не только от ряда экономических факторов, но и от уровня потреб­ления в предыдущем году (уt-1).

Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регу­лирования. Меняя их и управляя ими, можно заранее иметь целе­вые значения эндогенных переменных.

Структурная форма модели в правой части содержит при эн­догенных и экзогенных переменных коэффициенты bi и aj (bi ‒ коэффициент при эндогенной переменной, aj ‒ коэффициент при экзогенной переменной), которые называются структурные коэффициенты модели. Все переменные в модели выражены в от­клонениях от среднего уровня, т. е. под х подразумевается , а под у — соответственно . Поэтому свободный член в каждом уравнении системы отсутствует.

Использование МНК для оценивания структурных коэффи­циентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

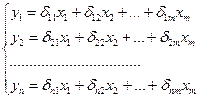
где ‒ 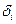коэффициенты приведенной формы модели.

По виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оценива­ются традиционным методом наименьших квадратов. Применяя МНК, можно оценить , а затем оценить значения эндогенных переменных через экзогенные.

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной фор­мы модели () через коэффициенты структурной модели (bi и aj). Для упрощения в модель не введены случайные переменные.

Для структурной модели вида:

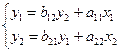
приведенная форма модели имеет вид:

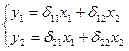
в которой у2 из первого уравнения структурной модели можно выразить следующим образом:

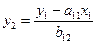
Тогда система одновременных уравнений будет представлена как:

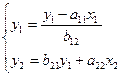
Отсюда имеем равенство:

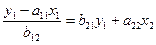
или

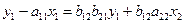
Тогда:

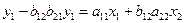
Или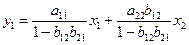

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

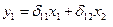
Из уравнения следует, что коэффициенты приведенной фор­мы модели представляют собой нелинейные соотношения коэф­фициентов структурной формы модели, т. е.

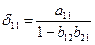и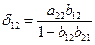

Аналогично можно показать, что коэффициенты приведенной формы модели второго уравнения системы (и ) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную у1 из второго структурного уравнения модели как

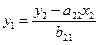
Запишем это выражение у1 в левой части первого уравнения структурной формы модели:

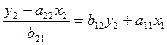
Отсюда:

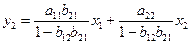
что соответствует уравнению приведенной формы модели:

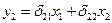
т. е.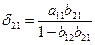

При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Иден­тификация — это единственность соответствия между приведен­ной и структурной формами модели.

С позиции идентифицируемости структурные модели можно подразделить на три вида:

· идентифицируемые;

· неидентифицируемые;

· сверхидентифицируемые.

Модель идентифицируема, если все структурные ее коэффици­енты определяются однозначно, единственным образом по коэф­фициентам приведенной формы модели, т. е. если число парамет­ров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты моде­ли оцениваются через параметры приведенной формы модели и модель идентифицируема. Рассмотренная выше структурная мо­дель

с двумя эндогенными и тремя экзогенными (предопределенными) переменными, содержащая шесть структурных ко­эффициентов, представляет собой идентифицируемую модель.

Модель неидентифицируема, если число приведенных коэф­фициентов меньше числа структурных коэффициентов, и в ре­зультате структурные коэффициенты не могут быть оценены че­рез коэффициенты приведенной формы модели. Структурная модель в полном виде содержащая n эндогенных и m предо­пределенных переменных в каждом уравнении системы, всегда неидентифицируема.

Модель сверхидентифицируема, если число приведенных ко­эффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно по­лучить два или более значений одного структурного коэффици­ента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Так, если в структур­ной модели полного вида

В ней пять структурных коэффициентов не могут быть одно­значно определены из шести коэффициентов приведенной фор­мы модели. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.

Структурная модель всегда представляет собой систему сов­местных уравнений, каждое из которых необходимо проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель счи­тается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверя­ется для каждого уравнения системы. Для того чтобы уравнение было идентифицируемо, нужно, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутству­ющих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других уравнениях, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие иден­тификации.