Спектральный анализ детерминированных гармонических сигналов с использованием ДПФ

6.1.2.1. Структура спектрального анализатора с использованием ДПФ

Предположим, что спектр аналогового сигнала x(t) сосредоточен в ограни­ченной полосе частот и, следовательно, может анализироваться с использованием дискретного эквивалента x[n], формируемого на выходе АЦП. Параметры АЦП выбираются таким образом, чтобы эффекты наложе­ния периодических копий спектра и шумы квантования по уровню могли не учитываться. Кроме того, будем полагать, что параметры гармонического сигнала ( амплитуда, фаза и частота) не изменяются во времени.

Спектральный анализ таких сигналов может быть выполнен с помощью дискретного преобразования Фурье (ДПФ). Причем для анализа используется взвешенная входная последовательность 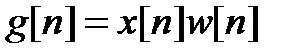, которая определяется как произведение дискретного сигнала x[n] на некоторую весовую функцию w[n] на конечном интервале N. В качестве средства оценивания спектра используется R-точечное ДПФ (БПФ), (R ³ N) (рисунок 2.1).

g[n]

´

Д П Ф   (БПФ)

w[n]

x[n]

. . .

g[0]

g[1]

g[R-1]

. . .

Канал 0

Канал 1

Канал R-1

Рисунок 2.1 – оценка спектра с использованием ДПФ

6.1.2.2. Частотная характеристика одного канала ДПФ

Рассмотрим формулу ДПФ в следующем виде:

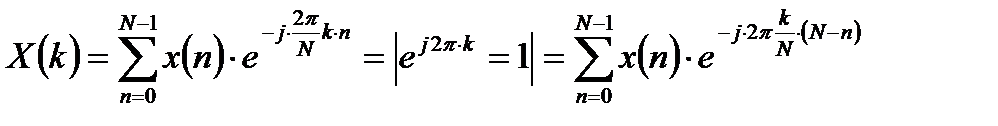. (2.1)

Выражение (2.1) для ДПФ представляет собой дискретную свертку и один из отсчетов спектра является выходным сигналом цифрового фильтра, импульсная характеристика которого определяется выражением:

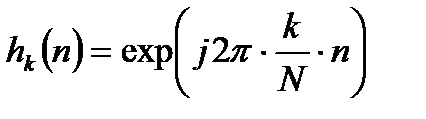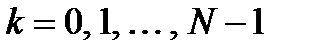, , (2.2)

где 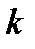- номер частотного отсчета.

Передаточная функция такого фильтра является z-преобразованием от импульсной характеристики:

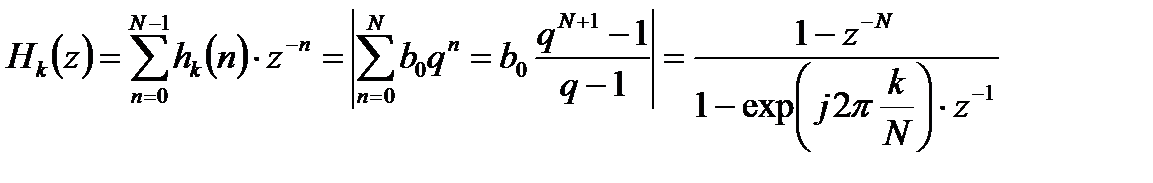. (2.3)

Частотную характеристику фильтра получим в результате использования подстановки :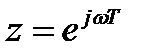

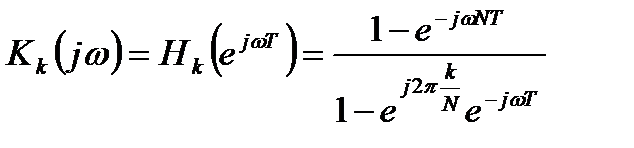. (2.4)

После выполнения преобразований АЧХ такого фильтра примет окончательный вид:

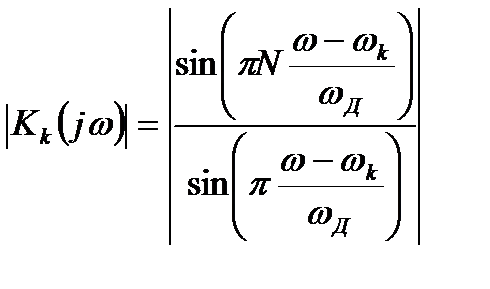, (2.5)

где 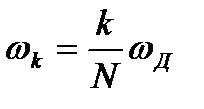- частота настройки k-ого фильтра;

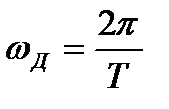- частота дискретизации входного сигнала.

График АЧХ одного из каналов ДПФ приведена на рисунке 2.2. Как видно из графика, АЧХ фильтра одного канала ДПФ имеет максимальный уровень боковых лепестков, равный:

.

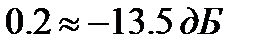Ширина главного лепестка АЧХ канала ДПФ определяет разрешающую способность спектрального анализа и определяется выражением:

.

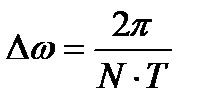Рисунок 2.2 – АЧХ одного из каналов ДПФ

6.1.2.3. Явление растекания спектра

При вводе понятия ДПФ предполагалось, что последовательность анализируемых отсчетов периодически продолжается за пределами окна анализа. Если значения начальных и конечных отсчетов сигнала сильно отличаются, то при периодическом продолжении сигналов возникают сильные скачки на стыках окон. Это приводит к явлению растекания спектра.

Пусть вычисляется спектр дискретного гармонического сигнала:

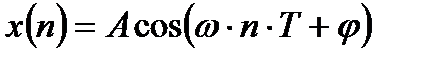. (2.6)

Пусть анализируемая последовательность содержит целое число периодов гармонического сигнала:

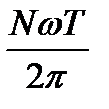- целое число.

В этом случае периодически продолженный сигнал не содержит скачков и характеризуется только двумя спектральными отсчетами, отличными от нуля:

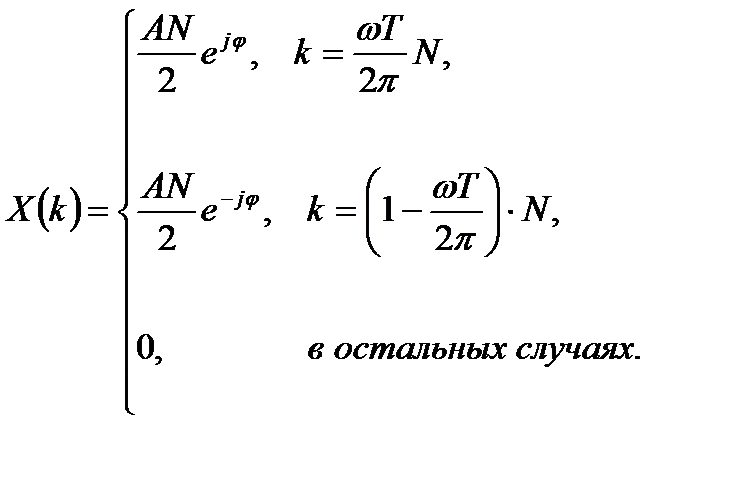
Таким образом, аналогично спектру непрерывного гармонического сигнала, ДПФ в этом случае отличается от нуля для двух значений 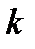, символизирующих положительную и отрицательную частоту.

Однако если величина 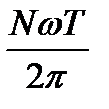не является целым числом, то дискретный спектр становится более сложным, так как в этом случае периодически продолженная последовательность не может являться отсчетами непрерывной синусоиды. Поэтому в дискретном спектре появляются дополнительные составляющие.

Примерные графики дискретного гармонического сигнала и модуля его спектра для случаев целого и нецелого числа периодов в пределах окна анализа приведены на рисунке 2.3.

Явление растекания спектра можно пояснить и с использованием спектров дискретизированных синусоид с различными частотами, спектры которых показаны на рисунке 2.4. Ранее было получено, что спектры дискретизированных сигналов представляют собой периодические непрерывные функции. Однако в случае целого числа периодов синусоиды в пределах окна анализа все дискретные значения отсчетов ДПФ попадают на границы между боковыми лепестками. При нецелом числе периодов синусоиды в пределах окна анализа этого не происходит.

Рисунок 2.3 – дискретный гармонический сигнал и его спектры

Рисунок 2.4 – спектры дискретизированных гармонических сигналов

6.1.2.4. Использование весовых функций

Для уменьшения явления растекания спектра при спектральном анализе с использованием ДПФ применяют весовые функции. В этом случае перед расчетом ДПФ сигнал 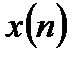умножается на весовую функцию :

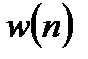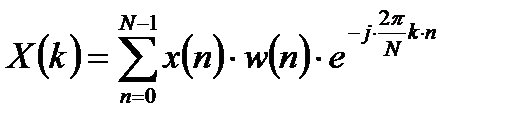. (2.7)

Используемая весовая функция является спадающей по краям анализируемого сегмента времени. Это приводит к ослаблению эффектов, связанных со скачком сигнала при его периодическом продолжении за пределами сегмента анализа.

Использование весовой функции приводит к уменьшению уровня боковых лепестков частотных характеристик, соответствующих отсчетам ДПФ. Выражение для частотной характеристики в этом случае должно учитывать весовую функцию:

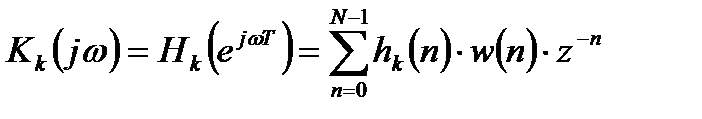. (2.8)

Платой за уменьшение уровня боковых лепестков частотных характеристик отдельных каналов ДПФ является расширение центрального лепестка частотной характеристики: рисунок 2.5.

Рисунок 2.5 – АЧХ одного из каналов ДПФ до и после использования весовой обработки

Наиболее известны следующие весовые функции:

· Хэмминга: 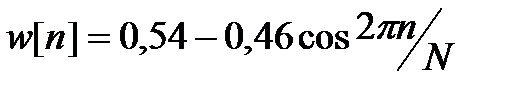, d_бл= -43 дБ;

· Блэкмана: 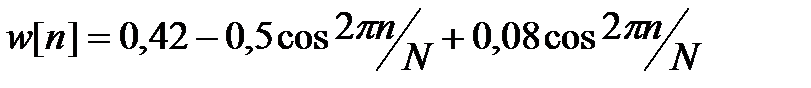, d_бл= -58 дБ.