Вычисление части линейной свертки и секционирование
Ранее предполагалось, что две функции, подлежащие свертке, имеют конечную длительность. Однако на практике входные данные имеют бесконечную длительность либо за счет непрерывного потока входных данных, либо за счет ограниченности доступной памяти устройства цифровой обработки, которая не может в себя вместить требуемый объем выборки. В таких случаях свертку можно выполнить поэтапно, разделив входные данные на отдельные блоки, выполнив необходимые вычисления для каждого блока и затем объединив результаты.
При использовании блочной фильтрации необходимо решать проблему формирования блоков и объединения выходных сигналов, полученных при обработке отдельных блоков.
Эти проблемы решаются двумя методами:
- методом перекрытия с суммированием (overlap-add);
- методом перекрытия с накоплением (overlap-save).
Для метода перекрытия с суммированием входной сигнал разбивается на неперекрывающиеся блоки длиной 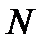 . Результаты линейной свертки отдельных блоков суммируются.
. Результаты линейной свертки отдельных блоков суммируются.
Так как входной сигнал разбивается на участки длины 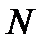 , а результаты фильтрации участков имеют длину
, а результаты фильтрации участков имеют длину 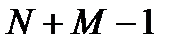 , то отфильтрованные сегменты перекрываются друг с другом в
, то отфильтрованные сегменты перекрываются друг с другом в 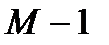 точках, причем для получения искомого результата налагающиеся друг на друга участки необходимо просуммировать. Поэтому такая процедура вычисления результата фильтрации называется перекрытием с суммированием: рисунок 3.1.
точках, причем для получения искомого результата налагающиеся друг на друга участки необходимо просуммировать. Поэтому такая процедура вычисления результата фильтрации называется перекрытием с суммированием: рисунок 3.1.
Перекрытие получается потому, что линейная свертка каждого участка получается длиннее, чем сворачиваемый участок. Метод перекрытия с суммированием в общем случае не привязан к ДПФ и циклической свертке. Однако может использоваться вычисление линейной свертки с применением быстрой круговой свертки.
Для метода перекрытия с накоплением входной сигнал разбивается на блоки длиной N, перекрывающиеся по краям на 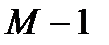 отсчетов (рисунок 3.2). У выходного сигнала для каждого блока, полученного методом круговой свертки, отбрасываются крайние «хвосты» по
отсчетов (рисунок 3.2). У выходного сигнала для каждого блока, полученного методом круговой свертки, отбрасываются крайние «хвосты» по 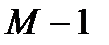 отсчетов. После этого выходные блоки объединяются без перекрытия: рисунок 3.3. Соответственно, перед круговой сверткой импульсная характеристика фильтра длиной М дополняется нулями до длины N.
отсчетов. После этого выходные блоки объединяются без перекрытия: рисунок 3.3. Соответственно, перед круговой сверткой импульсная характеристика фильтра длиной М дополняется нулями до длины N.
Рисунок 3.1 – Разложение входной последовательности на непересекающиеся сегменты длины N с последующей сверткой каждого сегмента
Рисунок 3.2 – Способ сегментации последовательности на перекрывающиеся участки длины 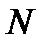 с накоплением
с накоплением
Рисунок 3.3 – Результат свертки каждого сегмента с импульсной характеристикой (зачеркнуты интервалы, сигналы которых отбрасываются при вычислении линейной свертки)
При проектировании возникает задача выбора оптимального по критерию минимума времени свертки значения 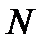 при фиксированном
при фиксированном 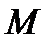 . При малых значениях
. При малых значениях 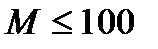 оптимальное значение длины блока определяется выражением
оптимальное значение длины блока определяется выражением 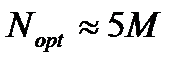 .
.
Литература
Маркович И.И. Цифровая обработка сигналов в системах и устройствах: монография / И.И. Маркович; Южный федеральный университет. – Ростов н/Д: Издательство Южного федерального университета, 2012. – 236 с. (стр. 138)
Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с. (с. 129)
