Цифровые фильтры. Методы реализации и синтеза фильтров
Проектирование цифровых фильтров
4.1.1. Основные определения проектирования ЦФ
Под цифровым фильтром (ЦФ) в широком смысле понимают любую цифровую систему, которая осуществляет извлечение цифрового сигнала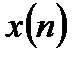 
либо его параметров из существующей на входе системы смеси 
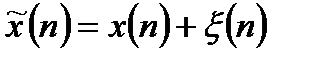сигнала с помехой.
Цифровой фильтр в узком смысле представляет собой частотно-избирательную цепь, обеспечивающую селекцию цифровых сигналов по частоте.
К цифровым фильтрам в широком смысле относят:
- амплитудные и фазовые корректоры частотных характеристик;
- дифференциаторы;
- преобразователи Гильберта;
- согласованные фильтры.
К цифровым фильтрам в узком смысле относят частотно-избирательные фильтры:
- фильтр нижних частот (ФНЧ);
- фильтр верхних частот (ФВЧ);
- полосовой фильтр (ПФ);
- режекторный фильтр (РФ).
Цифровые фильтры могут быть реализованы:
- аппаратно;
- программно;
- аппаратно-программно.
Аппаратная реализация подразумевает использование функциональных элементов в виде регистров, сумматоров, умножителей, устройств памяти, логических элементов.
Программная реализация означает, что фильтр представлен в виде программы, написанной на языке программирования.
Аппаратно-программная реализация означает выполнение части функций фильтра аппаратно (АЦП, ЦАП, умножение, прием/передача данных) при программном выполнении другой части функций.
Под проектированием ЦФ понимают процесс, в результате которого предъявляется программа или цифровое устройство, отвечающее заданным требованиям.
Проектирование ЦФ включает в себя этапы:
1. Синтез.
2. Разработка алгоритмов вычислений.
3. Проверка моделированием.
4. Практическая реализация и отладка.
Результатом синтеза является структурная схема фильтра и набор коэффициентов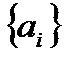 
и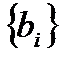 
разностных уравнений и передаточных функций.
Разработка алгоритма вычислений зависит от разрядности регистров, количества аккумуляторов процессора, возможности распараллеливания операций, наличия устройств перемножения и накопления. Конечный алгоритм должен обеспечить функционирование фильтра в реальном масштабе времени при минимальных потерях качества.
Проверка моделированием осуществляется в нереальном масштабе времени по стандартным сигналам с использованием программных эмуляторов. При этом устраняются логические ошибки и проверяется соответствие фильтра заданным характеристикам.
Практическая реализация и отладка осуществляется в реальном времени с помощью отладочных модулей.
Общие сведения о синтезе ЦФ
В процессе синтеза выполняются следующие действия:
- задаются требования к фильтру;
- рассчитываются коэффициенты передаточной функции или разностного уравнения;
- формируется структурная схема ЦФ.
Требования к ЦФ могут задаваться либо во временной, либо в частотной области в зависимости от назначения фильтра.
Требования во временной области задаются как правило к согласованным фильтрам через требуемую импульсную характеристику.
Требования в частотной области задаются как правило к частотно-избирательным фильтрам.
Например, требования к полосовому фильтру характеризуются пятью частотными полосами (рисунок 2.1):
- центральной полосой пропускания (ПП);
- двумя полосами задержания (ПЗ1, ПЗ2);
- двумя переходными полосами.
Рисунок 2.1 – диаграмма требований к АЧХ ПФ
На рисунке 1 обозначены:
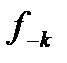- граничная частота первой полосы задержания ПЗ1, ширина которой 
;
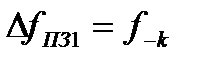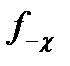- левая частота среза полосы пропускания;
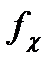- правая частота среза полосы пропускания, ширина полосы пропускания 
;
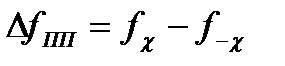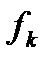- граничная частота второй полосы задержания ПЗ2, ширина которой 
;
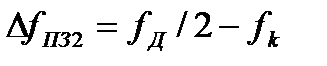Переходные полосы 1 и 2 имеют ширину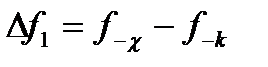 
, 
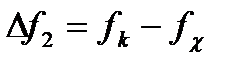, соответственно.
Величина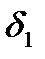 
характеризует максимально допустимое отклонение АЧХ от 1 в пределах полосы пропускания. Величина 
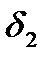характеризует максимально допустимое отклонение АЧХ от 0 в пределах полос задержания. Требования к характеристикам АЧХ в пределах переходных полос обычно не задаются.
Существуют следующие разновидности методов синтеза:
- прямые методы синтеза;
- методы синтеза с использованием аналогового прототипа.
Прямые методы делятся на две категории:
- оптимальные методы;
- субоптимальные методы.
В оптимальных методах численными методами ищется минимум заданной функции качества. В качестве минимизируемой меры отклонения характеристики фильтра от заданной используется норма ошибки:
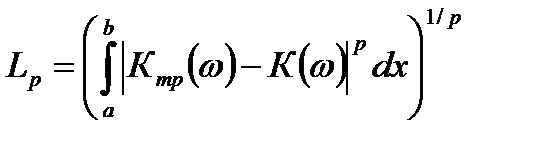. (2.1)
Субоптимальные методы позволяют упростить вычисления за счет учета специфики задачи.