БПФ с прореживанием по частоте

В БПФ с прореживанием по частоте выделяют в исходном ДПФ два слагаемых, соответствующих двум следующим друг за другом половинам исходной последовательности:

. (3.1)

Из второй суммы можно выделить множитель

.

Этот множитель равен 1 или -1 в зависимости от четности номера вычисляемого спектрального отсчета , поэтому в последующем четные и нечетные номера отсчетов частоты рассматриваются отдельно.

После выделения множителя ±1 комплексные экспоненты в обеих суммах (для четных и нечетных номеров спектральных отсчетов) становятся одинаковыми и их можно вынести за скобки:

, (3.2)

. (3.3)

Записанные суммы представляют собой ДПФ суммы и разности половин исходной последовательности, при этом разность перед вычислением ДПФ умножается на комплексные экспоненты . Каждое из двух используемых здесь ДПФ имеет размерность N/2.

Таким образом, при вычислении БПФ с прореживанием по частоте из исходной последовательности длиной N получают две последовательности и длиной N/2:

, (3.4)

. (3.5)

ДПФ последовательности дает спектральные отсчеты с четными номерами, ДПФ последовательности - с нечетными номерами:

, (3.6)

. (3.7)

Процесс вычисления 8-точечного ДПФ путем разбиения его на два 4-точечных ДПФ с прореживанием по частоте показан на рисунке 3.1.

Так как комплексный экспоненциальный множитель в данном алгоритме применяется к результату вычитания двух сигналов, то «бабочка» БПФ с прореживанием по частоте имеет другую структуру: рисунок 3.2.

Алгоритм БПФ с прореживанием по частоте применяется реже, чем с прореживанием по времени, так как в последнем случае на выходе получаем отсчеты ДПФ в естественном порядке следования.

Рисунок 3.1 – вычисление 8-точечного ДПФ с использованием двух 4-х точечных ДПФ путем прореживания по частоте

Рисунок 3.2 – условное обозначение «бабочки» и ее структурная схема при прореживании по частоте

Свойства БПФ

1. Наибольшее ускорение вычислений благодаря применению БПФ достигается при длине исходной последовательности, равной целочисленной степени 2. Снижение вычислительных затрат по сравнению с непосредственным использованием ДПФ составляет 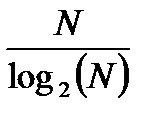раз.

2. Экономия вычислительных затрат достигается за счет объединения всех слагаемых, умножаемых на одинаковые множители и трансформации некоторых множителей в 1 или -1.

3. Если длина исходной последовательности – простое число, вычисление ДПФ возможно только по формуле ДПФ либо за счет дополнения исходной последовательности нулями.

4. БПФ не является приближенным алгоритмом. При отсутствии вычислительных погрешностей он дает точно такой же результат, что и исходное ДПФ.

5. Алгоритм БПФ предназначен для одновременного расчета всех спектральных отсчетов. Если необходимо получить лишь отдельные отсчеты, то может оказаться предпочтительной прямая формула ДПФ или известный алгоритм Герцеля.

Линейные дискретные системы