БПФ с прореживанием по времени
Основная идея алгоритма БПФ с прореживанием по времени заключается в поэтапном вычислении ДПФ на 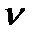 этапах, при этом на каждом последующем этапе ДПФ определяется через ДПФ вдвое меньшей размерности.
этапах, при этом на каждом последующем этапе ДПФ определяется через ДПФ вдвое меньшей размерности.
Пусть 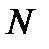 - четное число. Выделим в исходном ДПФ два слагаемых, соответствующих элементам исходной последовательности с четными и нечетными номерами:
- четное число. Выделим в исходном ДПФ два слагаемых, соответствующих элементам исходной последовательности с четными и нечетными номерами:
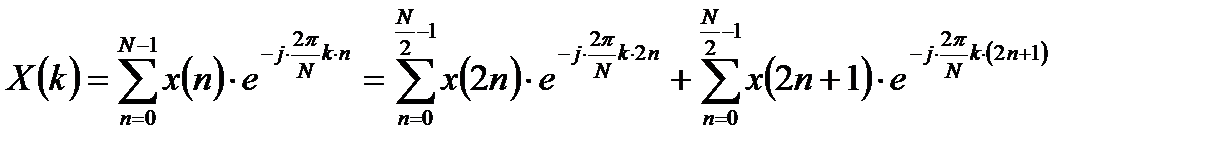 . (2.1)
. (2.1)
Введем обозначения 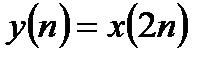 и
и 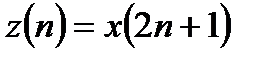 и вынесем из второй суммы множитель
и вынесем из второй суммы множитель 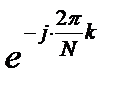 . В этом случае можно записать:
. В этом случае можно записать:
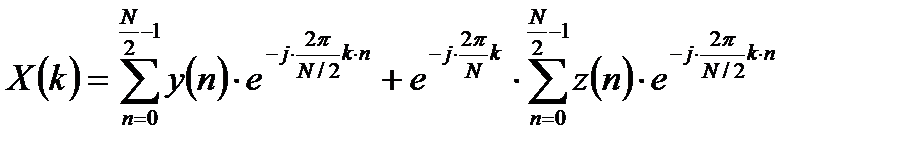 . (2.2)
. (2.2)
В последнем выражении две суммы представляют собой ДПФ последовательностей 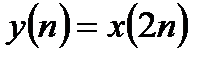 и
и 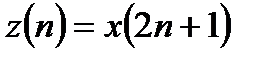 , причем каждое из ДПФ имеет размерность
, причем каждое из ДПФ имеет размерность 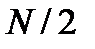 . Следовательно, можно записать:
. Следовательно, можно записать:
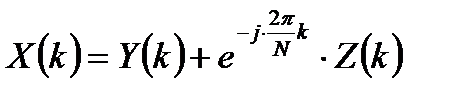 , (2.3)
, (2.3)
где 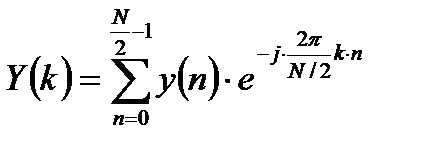 - ДПФ последовательности отсчетов с четными номерами;
- ДПФ последовательности отсчетов с четными номерами;
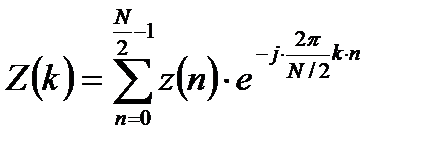 - ДПФ последовательности отсчетов с нечетными номерами.
- ДПФ последовательности отсчетов с нечетными номерами.
Так как ДПФ размерностью 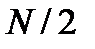 дает лишь
дает лишь 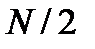 спектральных коэффициентов, то непосредственно использовать выражение (2.3) можно только при
спектральных коэффициентов, то непосредственно использовать выражение (2.3) можно только при 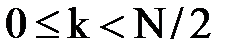 . Однако для остальных индексов
. Однако для остальных индексов 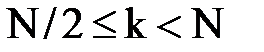 можно воспользоваться периодичностью спектра дискретного сигнала:
можно воспользоваться периодичностью спектра дискретного сигнала:
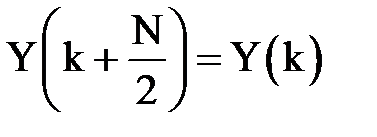 ,
,
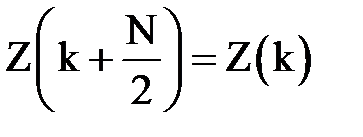 .
.
Соответственно, для аргументов 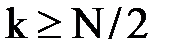 выражение (2.3) примет вид:
выражение (2.3) примет вид:
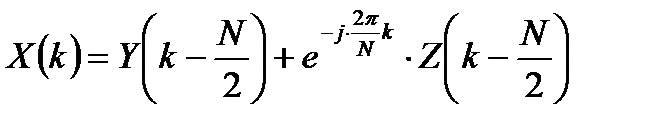 ,
, 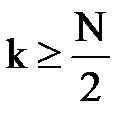 . (2.4)
. (2.4)
Процесс вычисления 8-точечного ДПФ путем его разбиения на два 4-точечных ДПФ иллюстрируется рисунком 2.1.
Рисунок 2.1 – вычисление 8-точечного ДПФ с использованием двух 4-х точечных ДПФ
Объединение результатов двух ДПФ реализуется с помощью 4-х дополнительных блоков. Каждый из блоков имеет два входных и два выходных сигнала. Один из входных сигналов умножается на комплексную экспоненту 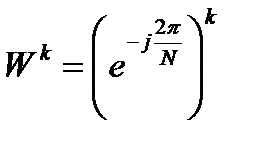 , после чего суммируется со вторым сигналом и вычитается из него, формируя два выходных сигнала. Это соответствует реализации формул (2.2) и (2.3). Данная операция получила название «бабочки». Структура бабочки представлена на рисунке 2.2.
, после чего суммируется со вторым сигналом и вычитается из него, формируя два выходных сигнала. Это соответствует реализации формул (2.2) и (2.3). Данная операция получила название «бабочки». Структура бабочки представлена на рисунке 2.2.
Рисунок 2.2 – условное обозначение «бабочки» и ее структурная схема при прореживании по времени
Определим количество операций на выполнение ДПФ рассмотренным способом. Каждое из двух ДПФ половинной размерности требует 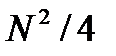 арифметических операций. Кроме того, при вычислении окончательных результатов каждый спектральный коэффициент
арифметических операций. Кроме того, при вычислении окончательных результатов каждый спектральный коэффициент 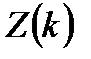 умножается на комплексный весовой множитель. Это добавляет
умножается на комплексный весовой множитель. Это добавляет 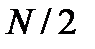 операций умножения. В результате имеется
операций умножения. В результате имеется
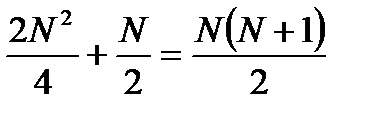
арифметических операций, что почти в 2 раза меньше, чем при вычислении ДПФ прямым способом.
Наибольшая степень ускорения вычислений может быть достигнута при продолжении деления последовательностей на две части до тех пор, пока не получатся двухэлементные последовательности. ДПФ двухэлементных последовательностей рассчитывается вообще без использования операции умножения за счет вычисления суммы и разности двух отсчетов:
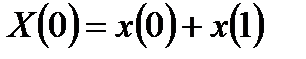 ,
,
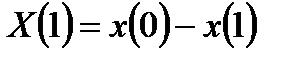 .
.
Любой из алгоритмов БПФ выполняется за следующее число этапов: 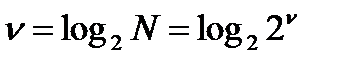 . Количество «бабочек», выполняемых на каждом этапе, одинаково и равно
. Количество «бабочек», выполняемых на каждом этапе, одинаково и равно 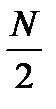 . Результирующее число требуемых при этом пар операций «умножение-сложение» можно оценить как
. Результирующее число требуемых при этом пар операций «умножение-сложение» можно оценить как
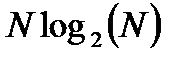 .
.
Таким образом, снижение вычислительных затрат по сравнению с использованием ДПФ составляет 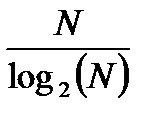 раз. Например, при
раз. Например, при 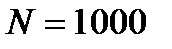 достигается ускорение вычислений в 102.4 раза.
достигается ускорение вычислений в 102.4 раза.
Экономия вычислительных затрат достигается за счет:
- объединения всех слагаемых, умножаемых на одинаковые множители;
- трансформации некоторых множителей в 1 или -1.
