Модель дискретного и дискретизированного сигналов во временной области

Введение

1.1. Предмет и задачи ЦОС

Цифровая обработка сигналов (ЦОС) – это область науки и техники, в которой изучаются общие для разных дисциплин алгоритмы и средства обработки сигналов на основе численных методов с использованием вычислительной техники.

Предмет исследований теории ЦОС полностью связан с самим процессом обработки цифровых сигналов в конкретной вычислительной среде и, как правило, не зависит от цели преобразования, которая определяется областью применения. Для разработчика системы или устройства ЦОС, реализующего заданный математический оператор преобразования, неважно как будут использоваться результаты преобразования, задача заключается прежде всего в минимизации вычислительных и аппаратурных затрат. При этом дополнительно могут учитываться отведенные ресурсы памяти программ и данных, а также допустимая погрешность измерений.

На основании анализа развития теории и техники ЦОС можно сделать следующие выводы:

- цифровая обработка сигналов – информатика реального времени – это научное направление, связанное с разработкой и оптимизацией алгоритмов преобразования цифровых сигналов с учетом особенностей их реализации;

- эволюция теории и техники ЦОС – это развитие и взаимное сближение математических методов обработки информации и компьютерных технологий на базе новых технических решений, использующих малые ЭВМ, микропроцессоры, цифровые процессоры обработки сигналов (ЦПОС) и программируемых логических интегральных схем (ПЛИС).

Задачи, которые необходимо решать на пути разработки устройств и систем ЦОС можно свести к следующим проблемам:

1. Представление аналогового сигнала в цифровой форме;

2. Выбор класса цифровых преобразований, обеспечивающих воспроизведение заданного оператора 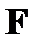с требуемой точностью (цифровые цепи с бесконечной или конечной импульсными характеристиками);

3. Аппроксимация математического оператора 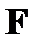в заданном классе цифровых цепей: характеристики реального оператора 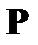могут отличаться от желаемых и задача аппроксимации заключается в расчете оптимальных параметров цифровой цепи, минимизирующих отклонение характеристик оператора 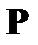от желаемого оператора ;

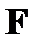4. Синтез структуры оператора 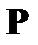и оптимизация ее параметров: воспроизведение желаемых характеристик оператора 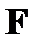с заданной точностью является основной целью синтеза структуры оператора 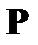и последующего расчета параметров цифровой цепи, которые могут быть реализованы различными путями, характеризуемыми разными затратами при практической реализации (объем вычислений в единицу времени, емкость памяти, потери из-за собственных шумов и округления коэффициентов);

5. Анализ влияния собственных шумов и неточного представления коэффициентов оператора 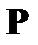на точность воспроизведения желаемых характеристик (анализ устойчивости, причин возникновения переполнений и предельных циклов, выбор масштабирующих множителей и разрядности представления данных и коэффициентов);

6. Синтез малошумящих и низкочувствительных к неточному представлению коэффициентов структур оператора преобразования ;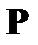

7. Выбор схемотехнического решения (класса сигнальных процессоров, семейства процессорных модулей, создания эффективного программного обеспечения).

В теории ЦОС обычно выделяют следующие разделы:

- дискретные сигналы;

- дискретное преобразование Фурье (ДПФ) и быстрое преобразование Фурье (БПФ);

- линейные дискретные системы;

- КИХ и БИХ фильтры;

- эффекты квантования в цифровых системах;

- спектральный анализ сигналов;

- многоскоростная обработка данных;

- адаптивная обработка сигналов;

- технология проектирования систем ЦОС на базе цифровых процессоров и программируемых логических интегральных схем (ПЛИС).

Иногда теорию ЦОС разделяют на две части: методы ЦОС и средства ЦОС. В этом случае вторая части теории ЦОС посвящается технология проектирования систем ЦОС на базе цифровых процессоров и программируемых логических интегральных схем.

1.2. История развития теории и техники ЦОС

Можно выделить следующие этапы развития теории и техники ЦОС.

0-й этап: начало пути. В 40-х годах появились первые ЭВМ, однако их ограниченные вычислительные ресурсы не позволяли проводить обработку сигналов в реальном масштабе времени. Речь шла только о моделировании реальных процессов. Только в 60-х годах появились малые ЭВМ, обеспечивающие обработку сигналов в реальном масштабе времени. Возможность обработки аналоговых по природе сигналов цифровыми методами привлекла внимание специалистов в области связи, гидроакустики и обработки речевых сигналов. С этого времени ЦОС формируется как самостоятельное научное направление.

1-й этап: цифровая фильтрация и спектральный анализ. На данном этапе развития (1965 – 1975 гг.) основной предметной областью ЦОС была цифровая фильтрация и спектральный анализ. Первый крупный вклад в теорию ЦОС внесли ученые Б. Голд и Ч. Рэйдер. Итоги первого этапа развития теории ЦОС подводит книга Л. Рабинера и Б. Голда. Позже появилось первое учебное пособие авторов А. Оппенгейма и Р. Шафера. Первые цифровые устройства обработки обладали низкой эффективностью и применялись как правило в военной области.

2-й этап: появление однокристальных микропроцессоров и становление современной теории ЦОС. В начале 70-х годов появляются первые однокристальные микропроцессоры (МП), а теория ЦОС входит в новый этап своего развития, который ограничен периодом с 1975 по 1985 г. В этот период формируются основные направления современной теории ЦОС.

3-й этап: оптимальное проектирование на сигнальных процессорах. В первой половине 80-х годов фирма Texas Instruments (США) объявила о промышленном выпуске первых сигнальных процессоров TMS32010 и открыла новую эру в технике ЦОС – эру СБИС обработки сигналов. Теория ЦОС все в большей степени развивается в направлении практического использования имеющихся СБИС с учетом имеющихся ресурсных ограничений. Методы и техника ЦОС из военной области переходит в сферу интенсивных коммерческих разработок. Произошел прорыв в области методологии и техники проектирования систем ЦОС. Создаются мощные программные средства поддержки автоматизированного проектирования.

4-й этап: оптимальное проектирование на ПЛИС. Современный этап развития теории и техники ЦОС со второй половины 90-х годов отличается применением архитектурно перепрограммируемых СБИС цифровой обработки сигналов на базе программируемых логических интегральных схем (ПЛИС).

ПЛИС обработки сигналов прочно занимают положение между специализированными заказными СБИС и универсальными цифровыми процессорами обработки сигналов, вытесняя с рынка высоких технологий сигнальные процессоры. Системы на ПЛИС сочетают в себе сверхвысокую производительность заказных СБИС и высокую гибкость цифровых процессоров обработки сигналов, а также возможность размещения на кристалле всей структуры системы, включая нестандартную периферию.

В случаях, когда система ориентирована на решение сложных, разветвленных алгоритмов обработки в реальном времени на различных скоростях потоков входных данных, наивысшая эффективность достигается совместным использованием ПЛИС и сигнальных процессоров.

Литература: Цифровая обработка сигналов – информатика реального времени. / Цифровая обработка сигналов. - 1999. - №1. – с. 5 – 17.

1.3. Общая структура системы ЦОС

Системы цифровой обработки сигналов оперируют с последовательностями цифровых кодов, которые называют цифровыми сигналами. Цифровой сигнал образовывается в результате аналого–цифрового преобразования непрерывных сигналов. Аналого-цифровое преобразование (АЦП) включает три этапа:

- дискретизацию сигнала по времени;

- квантование по уровню;

- цифровое кодирование.

На первом этапе образуется дискретный сигнал x(nT_d), который является функцией дискретной переменной nT_d, принимающей только фиксированные значения. В этом случае дискретный сигнал определяют функцией номера отсчета x(n). Говорят, что T_¶=1/f_¶ это период дискретизации, f_¶ - частота дискретизации, а n - номер отсчета.

Второй этап АЦП дает дискретный квантованный сигнал x_кв(nT_¶), отличающийся конечным множеством принимаемых им значений.

На третьем этапе получается цифровой сигнал x_ц(nT_¶) в виде последовательности цифровых кодов с заданным числом разрядов.

Вычислительные средства в соответствии с заданным алгоритмом цифровой обработки F преобразуют сигнал x_ц(nT_¶) в выходной цифровой сигнал y_ц(nT_¶) = F{x_ц(nT_¶)}.

В цифровых системах с аналоговым выходом цифровой выходной сигнал y_ц(nT_¶) преобразуется в аналоговый сигнал y(t) с помощью цифро-аналогового преобразования (ЦАП).

Процесс обработки дискретных сигналов можно представить в следующей последовательности. Каждому отсчёту ставится в соответствие двоичное кодовое слово, а действия над отсчётами заменяются на действия над кодовыми словами. Дискретная цепь становится цифровой цепью, цифровым фильтром (ЦФ). Перевод отсчётов в двоичные кодовые слова происходит в аналогово-цифровом преобразователе (АЦП). На выходе ЦФ осуществляется обратная операция: кодовые слова в цифро-аналоговом преобразователе превращаются в отсчёты дискретного сигнала и, наконец, на выходе, синтезирующего фильтра (СФ) формируется обработанный аналоговый сигнал.

Рисунок 1.4 – общая структура системы ЦОС

Литература

Якимов Е.В. Цифровая обработка сигналов: учебное пособие / Е.В. Якимов, Г.В. Вавилова, И.А. Клубович. – Томск: Изд-во Томского политехн. ун-та, 2008. – 307 с. (с. 20)

1.4 . Области применения и возможности ЦОС.

Область применения ЦОС определяется видами радиотехнических систем:

- системы передачи информации;

- системы радиолокации;

- системы радионавигации;

- системы радиоуправления;

- системы разрушения информации.

В каждом виде радиотехнических систем методами ЦОС могут решаться следующие задачи:

- задачи первичной обработки сигналов (фильтрация сигналов на этапах внутрипериодной и междупериодной обработок);

- задачи вторичной обработки сигналов (обнаружение, разовое измерение, фильтрация и экстраполяция разовых измерений).

Типовыми алгоритмами, использующимися при ЦОС являются алгоритмы:

- свертки;

- линейной фильтрации;

- спектрального преобразования и анализа.

По сравнению с аналоговой обработкой сигналов имеют место следующие преимущества ЦОС:

- гарантированная инструментальная точность, зависящая от используемой разрядности чисел;

- высокая стабильность характеристик за счет отсутствия параметрических уходов из-за влияния температуры, старения;

- возможность реализации сложных алгоритмов обработки;

- высокая гибкость с возможностью перепрограммирования цифровых устройств без изменения оборудования;

- возможность запоминания и задержки сигналов на неограниченное время;

- полная и неоднократная воспроизводимость сигналов без ухудшения качества;

- высокая надежность, малые размеры, стоимость и энергопотребление;

- автоматизация проектирования и эксплуатации.

К недостаткам ЦОС относят:

- ограниченная ширина полосы обрабатываемых сигналов;

- дополнительная погрешность из-за ограниченной разрядности аналого-цифровых и цифро-аналоговых преобразователей.

Карташов В.Г. Основы теории дискретных сигналов и цифровых фильтров. – М.: Высш. школа, 1982. – 109. (с. 12)

Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с. (с. 8)

1.5. Рекомендованная литература.

Минимально необходимые сведения о теории дискретной обработке сигналов и о цифровой фильтрации на фоне общих сведениях о сигналах и их обработке приведены в учебных пособиях по курсу «Радиотехнические цепи и сигналы». Наиболее удачными пособиями является следующие:

Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы: Учебник для вузов. – М.: Радио и связь, 1994.

Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. Для вузов по спец. «Радиотехника». – 3-е изд., перераб. и доп. – М.: Высш. шк., 2000. – 462 с.: ил.

Карташов В.Г. Основы теории дискретных сигналов и цифровых фильтров. – М.: Высш. школа, 1982. – 109.

Первый крупный вклад в теорию ЦОС внесли ученые Б. Голд и Ч. Рэйдер в своей книге:

Голд Б., Рэйдер Ч. Цифровая обработка сигналов / Пер. с англ.; Под ред. А.М. Трахтмана. – М.: Сов. Радио, 1973, 368 с.

Итоги первого этапа развития теории ЦОС подводит книга Л. Рабинера и Б. Голда:

Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов / Пер. с англ.; Под ред. Ю. И. Александрова. – М.: Мир, 1978.

Последние две книги не потеряли своей актуальности, в них подробно изложена теория дискретных сигналов, дискретной фильтрации и дискретного спектрального анализа. Главы, посвященные аппаратной реализации ЦОС, являются устаревшими.

Позже появилось первое учебное пособие авторов А. Оппенгейма и Р. Шафера:

Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. М.: Связь, 1979. – 416 с.

В последние годы в Санкт-Петербурге изданы современные учебники А.Б. Сергиенко и коллектива авторов во главе с А.И. Солониной:

Сергиенко А.Б. Цифровая обработка сигналов / А.Б. Сергиенко. – Спб.: БХВ -Петербург, 2011.768 с.

Основы цифровой обработки сигналов. Курс лекций / А.И. Солонина, Д.А. Улахович, С.М. Арбузов и др. – Спб.: БХВ – Петербург, 2005.768 с.

Солонина А.И., Арбузов С.М. Цифровая обработка сигналов. Моделирование в MATLAB / А.И. Солонина, С.М. Арбузов. – СПб.: БХВ – Петербург, 2008. 816 с.

Учебные пособия Солониной А.И. носят более полный, строгий и подробный характер и содержат некоторые факультативные вопросы цифровой обработки. Однако пособие Сергиенко А.Б. являются более методичными с точки зрения восприятия материала, что подтверждается ссылками Солониной А.И. на этого автора. Учебное пособие Солониной А.И. содержит список литературы из 53 источников. В пособии Сергиенко А.Б. приводится характеристика основных рекомендованных к использованию книг общим количеством 19 без ссылок на них в тексте.

Имеется следующее учебное пособие, объединяющее сведения о методах и средствах ЦОС и ориентированное на обработку речевых сигналов и изображений:

Бондарев В., Трестер Г., Черняга В. Цифровая обработка сигналов: методы и средства. – Х.: Конус, 2001. – 398 с.

Удачным является учебное пособие, оптимизированное по объему и качеству излагаемого материала:

Глинченко А.С. Цифровая обработка сигналов: в 2 ч. Ч.1. Красноярск: Изд-во КГТУ. 2001. 199 с.

Глинченко А.С. Цифровая обработка сигналов: в 2 ч. Ч.2. Красноярск: ИПЦ КГТУ. 2001. 184 с.

В учебнике приводится обширный список литературы (61 в Ч.1 и 46 в Ч.2), на который по тексту делаются ссылки, что способствует углубленному изучению материала в случае необходимости. Учебник в большей степени направлен на практическое применение методов цифровой обработки по сравнению с предыдущими авторами Солониной А.И. и Сергиенко А.Б. Как правило, приводятся структурные схемы алгоритмов программной реализации цифровой обработки сигналов.

Кривошеев В.И., Медведев С.Ю. Цифровая обработка сигналов. Лекции. 2002. – 241 с.

Подробно АЦП. Есть цифровые процессоры. Основная часть глубоко и хорошо изложена.

Баженов А.В. Цифровые методы реализации пространственно-временной обработки сигналов в авиационных радиоэлектронных комплексах / Ставрополь: СВВАИУ, 2006. – 219 с.

Рассмотрены классические разделы ЦОС без корреляции с остальными авторами. Подробно рассматриваются периодическая свертка и секционирование. Подробно рассмотрены классификация и варианты практической реализации ЦОС.

Якимов Е.В. Цифровая обработка сигналов: учебное пособие / Е.В. Якимов, Г.В. Вавилова, И.А. Клубович. – Томск: Изд-во Томского политехн. ун-та, 2008. – 307 с.

При самостоятельном изучении ЦОС возникает проблема выбора соответствующей литературы. Большинство авторов книг по ЦОС стремится изложить максимальное количество сведений с использованием усложненной обобщенной теории. При самостоятельном изучении дисциплины это может вызвать трудности в понимании материала. Учебное пособие Якимова Е.В. позволяет обеспечить самостоятельную подготовку студентов по магистерской программе по дисциплине «Цифровая обработка сигналов». В пособии излагаются основы теории математического описания цифровых систем, методов синтеза фильтров, теории БПФ и его применений, особенности аппаратной реализации систем ЦОС на основе специализированных процессоров. В пособии приведены примеры анализа и расчета цифровых систем. В приложении даны методические рекомендации по выполнению лабораторных работ.

Гетманов В.Г. Цифровая обработка сигналов: Учебное пособие. Изд. 2-е, расш. и перераб. М.: НИЯУ МИФИ, 2010. – 232 с.

Оригинальный незаимствованный материал по основным разделам дисциплины. Каждый раздел сопровождается контрольными вопросами по усвоению материала.

Микулович В.И. Цифровая обработка сигналов: курс лекций / В.И. Микулович. – Минск: БГУ, 2011. – 447 с.

Рассмотрены классические разделы ЦОС. Как правило, выводятся соотношения, но простым и наглядным образом.Много иллюстраций и примеров. Дополнительно рассмотрены вопросы практической реализации на процессорах и описываются основные особенности различных вариантов процессоров. Подробно рассматривается вопрос выбора частоты дискретизации и разрядности.

Маркович И.И. Цифровая обработка сигналов в системах и устройствах: монография / И.И. Маркович; Южный федеральный университет. – Ростов н/Д: Издательство Южного федерального университета, 2012. – 236 с.

Монография Марковича И.И. написана на базе лекций и кроме основных положений теории цифровой обработки сигналов содержит результаты ее практического использования в различных системах и устройствах. Рассматриваются спектральные характеристики шумов квантования АЦП, цифровой фильтр Герцеля, цифровое формирование квадратурных составляющих, цифровая обработка сигналов в РЛС. Блестяще рассмотрены характеристики фильтров с линейными фазочастотными характеристиками.

Бизин А.Т. Введение в цифровую обработку сигналов / Сибирская Государственная Академия телекоммуникаций и информатики. – Новосибирск, 1998. – 40 с.

Обсуждены основные положения теории дискретных сигналов и способы их обработки. Рассмотрены особенности цифровой реализации дискретных систем. Изложены методы расчета цифровых фильтров, получившие наибольшее распространение. Эффекты конечной разрядности ЦФ и их учет рассмотрены применительно к системам с фиксированной запятой, подробно рассмотрены вопросы масштабирования и каскадного представления фильтров. Обсуждены погрешности дискретизации и восстановления сигналов. Каждый вопрос, как правило, иллюстрирован численным примером и задачей (в том числе для метода перекрытия с накоплением при секционировании). В том числе рассмотрены фильтры с линейной фазой.

Малинкин В.Б. Основы адаптивной цифровой обработки сигналов: Учебное пособие / Сиб ГУТИ. – Новосибирск, 2010 г. – 202 с.

Васильев К.К. Методы обработки сигналов: Учебное пособие. – Ульяновск, 2001. – 80 с.

Рассматривается синтез и анализ алгоритмов обнаружения сигналов и оценивания их постоянных или изменяющихся параметров. Особое внимание уделено проблемам представления и рекуррентного оценивания гауссовских марковских процессов. Приводятся примеры применения результатов для реализации задач обработки сигналов в радиотехнических системах.

Тропченко А.Ю., Тропченко А.А. Цифровая обработка сигналов. Методы предварительной обработки. Учебное пособие по дисциплине «Теоретическая информатика»: СПб: СПбГУ ИТМО, 2009. – 100 с.

Борисов Д.Н., Винокурова Н.Н. Цифровая обработка сигналов. Конспект лекций. Учебно-методическое пособие для вузов. Издательско-полиграфический центр Воронежского государственного университета, 2010. – 99 с.

Капустин А.С. Методы цифровой обработки сигналов в радиотехнических системах: электрон. Учеб. пособие / А.С. Капустин, Д.В. Корнилин, И.А. Кудрявцев; Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С.П. Королева. – Самара, 2012.

С помощью пособия магистрантам предоставляется возможность изучения теоретических основ построения устройств дискретных систем, используемых в радиотехнических системах, а также методов линейной и нелинейной цифровой обработки сигналов.

Гадзиковский В.И. Цифровая обработка сигналов. М.: СОЛОН-ПРЕСС, 2013. – 766 с.

Рассмотрены алгоритмы цифрового моделирования аналоговых систем (с. 155). Рассматриваются вопросы синтеза цифровых фильтров среде MATLAB. Аппроксимация селективных цепей ПЧ рассматривается на с. 608. Методы синтеза скалярных нерекурсивных и рекурсивных цифровых фильтров подвергнуты методической переработке автором. При этом многие результаты впервые получены автором. Новизна результатов в основном обусловлена проектированию комплексных цифровых фильтров. Блестяще рассмотрены фильтры с линейной ФЧХ. При классификации дополнительно рассматриваются минимально-фазовые и неминимально-фазовые фильтры. Неплохо детализировано БПФ с прореживанием по времени и частоте. Подробно рассматривается использование пакета MATLAB для проектирования цифровых фильтров. Детально рассматриваются эффекты ограниченной разрядности. У автора имеется книга: Гадзиковский В.И. Методы проектирования цифровых фильтров. – М.: Горячая линия – Телеком, 2012. – 416 с.

Наиболее последними разработками курса цифровой обработки сигналов являются следующие учебные пособия:

Основы цифровой обработки сигналов: учебное пособие / Ю.А. Брюханов, А.А. Приоров, В.И. Джиган, В.В. Хрящев; Яросл. гос. ун-т им. П.Г. Демидова. - Ярославль: ЯрГУ, 2013. – 344 с.

Пособие отличается более глубоким и доступным рассмотрением некоторых основных разделов дисциплины, направлено на лучшее и углубленное понимание предмета, однако некоторые разделы отсутствуют. Наиболее глубоко рассмотрен раздел адаптивной цифровой обработки сигналов.

Цифровая обработка сигналов. Южный федеральный университет. Ростов-на-Дону, 2013. – 81 с.

Коберниченко В.Г. Расчет и проектирование цифровых фильтров: [учеб. - метод. пособие] / В.Г. Коберниченко. – Екатеринбург: Изд-во Урал. ун-та, 2013. – 64 с.

Затрагиваются вопросы использования функций МАТЛАБ для расчета цифровых фильтров.

Сюзев В.В. Основы теории цифровой обработки сигналов. Учебное пособие: - М.: Издательство «РТСофт», 2014. – 752 с.

В основном сложно о простом. Подготовлено на основе многолетнего опыта чтения лекций по ЦОС в МГТУ им. Н.Э. Баумана. Содержит оригинальные сведения из теории ортогональных базисных функций. Рекурсивная фильтрация приведена в сжатом виде.

Умняшкин С.В. Основы теории цифровой обработки сигналов: Учебное пособие. Москва: ТЕХНОСФЕРА, 2016. – 528 с.

Видеолекции по цифровой обработке сигналов доцента МФТИ Романюк Юрия Андреевича расположены по электронному адресу: http://lectoriy.mipt.ru/course/RadioTechnology-DigitalSignalProcessing-15L#lectures. Видеолекции этого же автора по математическим основам цифровой обработки сигналов расположены по электронному адресу: http://lectoriy.mipt.ru/course/RadioTechnology-MathDigitalSignalProcessing14L#lectures.

Manolakis, Dimitris G. Applied digital signal processing: theory and practice / Dimitris G. Manolakis, Vinay K/ Ingle. New York: Cambridge University Press – 2011/ - 990 p.

Orhan Gazi. Understanding Digital Signal Processing / Springer Nature Singapore Pte Ltd. 2018. – 310 p.

Sampling, multirate, DFT, Filter Design.

Справочник по радиолокации / Под ред. М.И. Сколника. Пер. с англ. под общей ред. В.С. Вербы. В 2 книгах. Книга 2. Москва: Техносфера, 2014. – 680 с. (Гл.25. Цифровая обработка радиолокационных сигналов).

Richard M.A. Principles of Modern Radar. Vol. 1: Basic Principles. Published by SciTech Publishing. Edison, NJ. 2010. – 924 p. (Part IV. Signal and Data Processing). В том числе имеется обзор элементной базы при реализации ЦОС.

Достоинством следующей книги является обширный материал практического применения методов цифровой обработки сигналов при проектировании микропроцессорных систем цифровой обработки:

Петровский А.А. Методы и микропроцессорные средства обработки широкополосных и быстропротекающих процессов в реальном времени / Под ред. Г.В. Римского. – Мн.: Наука и техника, 1988. – 272 с.

Вопросы практического проектирования цифровых фильтров и устройств рассматриваются в следующем справочнике:

Цифровые фильтры и устройства обработки сигналов на интегральных микросхемах: Справочное пособие / Ф.Б. Высоцкий, В.И. Алексеев, В.Н. Пачин и др.; Под ред. Ф.Б. Высоцкого. – М.: Радио и связь, 1984. – 216 с., ил.

Подробные сведения о функциях цифровой обработки приведены в MATLAB справочниках:

Солонина А.И. Цифровая обработка сигналов и MATLAB: учеб. Пособие / А.И. Солонина, Д.М. Клионский, Т.В. Меркучева, С.Н. Перов. – СПб.: БХВ - Петербург, 2013. – 512 с.: ил.

Солонина А.И. Цифровая обработка сигналов. – Моделирование в Simulink. – СПб.: БХВ – Петербург. 2012. – 432 с.

Дьяконов В.П. Matlab 6.5 SP 1/7 + Simulink 5/6 в математике и моделировании / В.П. Дьяконов. – М.: СОЛОН-Пресс, 2005. - 576 с.

Потемкин В.Г., Рудаков П.И. Система MATLAB 5 для студентов / В.Г. Потемкин, П.И. Рудаков. – М.: Диалог – МИФИ, 1999. - 448 с.

Дьяконов В. MATLAB. Обработка сигналов и изображений. Спец. справочник. – СПб.: Питер, 2002. – 608 с.

Рудаков П.И., Сафонов И.В. Обработка сигналов и изображений. MATLAB 5.х / Под общей ред. к.т.н. В.Г. Потемкина. – М.: ДИАЛОГ – МИФИ, 200. – 416 с.

Акчурин Э.А. Программирование в системе MATLAB. Компьютерное моделирование цифровых устройств. Методические указания к лабораторным работам / Самара: Поволжский Государственный Университет Телекоммуникаций и Информатики, - 2012. – 156 с.

Бадейкин. Синтез и анализ цифровых фильтров с использованием программного пакета Matlab. – 41 с.

Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ – Петербург, - 2005. – 320 с.

Кошкидько В.Г. Основы программирования в системе MATLAB: учебное пособие / Кошкидько В.Г., Панычев А.И.; Южный федеральный ун-т. – Таганрог: Издательство Южного федерального университета, 2016. – 84 с.

Дащенко А.Ф. MATLAB в инженерных и научных расчетах / Одесса: Астропринт, - 2003. – 212 с.

Kumar B.P. Digital Signal Processing Laboratory. Second Edition. CRC Press. Taylor & Francis Group. Boca Raton London New York. – 2010. - 278 p.

Кроме сведений и применении MATLAB при цифровой обработке, содержит описание разработки с использованием микропроцессора TMS320C6711 и описывает использование MATLAB в этом процессе.

http://matlab.ru MATLAB и Simulink – основные инструменты для вычислений в вузах во всем мире. Продукты MathWorks ускоряют темп обучения, преподавания и исследований в инженерных дисциплинах и науке в более чем 5000 университетов и колледжей. Продукты MathWorks также помогают готовить студентов к успешной карьере в отрасли, т.к. эти инструменты широко используются для научных исследований и разработок. Получив доступ к богатым возможностям моделирования и вычислений среды MATLAB и Simulink, студенты решают задачи из реальной практики и развивают навыки программирования. Студенты экспериментируют с алгоритмами, моделями и данными, пробуют разные сценарии.

Теории, методам и технической реализации цифровой обработки сигналов посвящен научно-технический журнал «Цифровая обработка сигналов», размещенный по электронному адресу: http://www.dspa.ru .

В России организована и ежегодно проводится Международная научно-техническая конференция «Цифровая обработка сигналов и ее применение – DSPA», содействующая общению специалистов, выявлению общих тенденций и направлений развития методов и техники ЦОС: http://www.dspa.ru/DSPA/dsparu/dsparu.php; http://www.rntores.ru. Доклады конференции доступны по электронному адресу: http://www.autex.spb.su/dspa/dspa.php.

Разработкой, производством аппаратно-программных средств сбора и цифровой обработки сигналов занимается ЗАО «Инструментальные системы», сайт которого размещен по адресу: http://www.insys.ru . Базируясь на современном опыте разработки аппаратуры цифровой обработки сигналов, новейшей элементной базе, программных средствах, компания «Инструментальные Системы» вышла на мировой уровень разработок и производства продукции.

Образовательный сайт, посвященный разработке цифровых устройств на ПЛИС фирмы Altera: http://marsohod.org/home.

Woods R., McAllister J., Lightbody G., Ying Yi. FPGA – based Implementation of Signal Processing Systems. Second Edition / 2017 John Willey&Sons, Ltd. – 488 p.

Соловьев В.В. Архитектуры ПЛИС фирмы Xilinx: CPLD и FPGA 7-ой серии. – М.: Горячая линия – Телеком, 2016. – 392 с.: ил.

Строганов А.В. Цифровая обработка сигналов в базисе программируемых логических интегральных схем: Учебное пособие. – 2-е изд., испр. и доп. – СПб.: Издательство «Лань», 2015. – 310 с.

Дискретные сигналы

2.1. Описание дискретных сигналов

Дискретные сигналы могут описываться во временной области, в спектральной области и с использованием z – преобразования.

Общие сведения о БПФ

Термином «быстрое преобразование Фурье» (БПФ) описывают алгоритмы вычисления дискретного преобразования Фурье, обеспечивающие экономию в требуемом числе арифметических операций и в первую очередь операций умножения.

Для вычисления одного коэффициента ДПФ необходимо выполнить операций комплексного умножения и суммирования. Таким образом, расчет всего ДПФ, содержащего коэффициентов, потребует 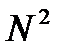пар операций «умножение – сложение».

Однако, если 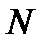не является простым числом и может быть разложено на множители (в частности, является целочисленной степенью 2: 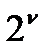, 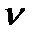- целое число), то процесс вычислений можно ускорить, разделив исходную последовательность на части, вычислив для них ДПФ и объединив результаты.

При реализации БПФ возможно несколько вариантов организации вычислений в зависимости от способа деления исходной последовательности на части (прореживание по времени или по частоте) и от того, на сколько фрагментов производится разбиение последовательности на каждом шаге (основание БПФ).

Первый алгоритм БПФ с основанием 2, известный как алгоритм БПФ Кули-Тьюки был опубликован в 1965 г в США учеными Кули и Тьюки.

Свойства БПФ

1. Наибольшее ускорение вычислений благодаря применению БПФ достигается при длине исходной последовательности, равной целочисленной степени 2. Снижение вычислительных затрат по сравнению с непосредственным использованием ДПФ составляет 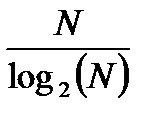раз.

2. Экономия вычислительных затрат достигается за счет объединения всех слагаемых, умножаемых на одинаковые множители и трансформации некоторых множителей в 1 или -1.

3. Если длина исходной последовательности – простое число, вычисление ДПФ возможно только по формуле ДПФ либо за счет дополнения исходной последовательности нулями.

4. БПФ не является приближенным алгоритмом. При отсутствии вычислительных погрешностей он дает точно такой же результат, что и исходное ДПФ.

5. Алгоритм БПФ предназначен для одновременного расчета всех спектральных отсчетов. Если необходимо получить лишь отдельные отсчеты, то может оказаться предпочтительной прямая формула ДПФ или известный алгоритм Герцеля.

Линейные дискретные системы

Структурные схемы ЛДС

ЛДС может быть реализована аппаратным или программным способами. В первом случае используются микросхемы в виде регистров, умножителей, сумматоров. Во втором случае составляется программа расчета с указанием, какие операции и в какой последовательности необходимо выполнить, причем элемент задержки соответствует ячейке памяти для хранения отсчетов.

По одному уравнению при аппаратной реализации можно разработать ЛДС с различным числом регистров и сумматоров, а значит с различным временем обработки, габаритными размерами и ценой.

При программной реализации ЛДС различия в структурных схемах приводят к различиям в быстродействии и ошибках, обусловленных конечной разрядностью.

Следовательно, выбор оптимальной структуры ЛДС является актуальной задачей.

Утверждается, что для ЛДС второго порядка существует около 100 вариантов структурных схем.

Сложность реализации некоторых вариантов структурных схем ЛДС отображена в Таблице 3.1.

Таблица 3.1. Сложность структурной реализации ЛДС

	Прямая форма	Обращенная форма	Каноническая форма 1	Каноническая Форма 2
Элементы задержки	2N	2N	N	N
Число умножений	2N+1	2N+1	2N+1	2N+1
Сумматоры		2N		N+1
Число точек распределения сигналов	2N		N+1

Рассмотрим наиболее распространенные варианты структурных схем ЛДС.

3.2.3.1. Прямая и обращенная структуры ЛДС

Прямая структура основана на представлении передаточной функции ЛДС в общем виде:

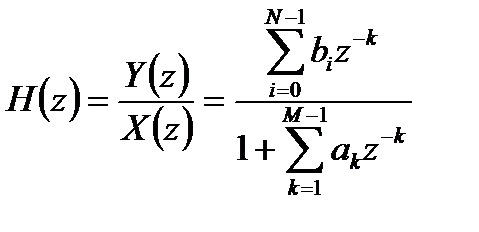. (3.1)

Такой передаточной функции соответствует разностное уравнение вида:

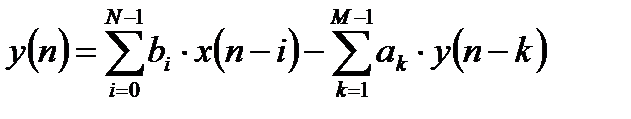. (3.2)

Прямая структура ЛДС 2-го порядка, соответствующая записанным передаточной функции общего вида и разностному уравнению, имеет вид, приведенный на рисунке 3.1.

Рисунок 3.1а – прямая структура рекурсивного фильтра 2-го порядка

Выходом ЛДС с прямой структурой является выход сумматора. В прямой форме структурной схемы четко выделены нерекурсивная и рекурсивная части. В прямой структуре ЛДС в линиях задержки хранятся непосредственно отсчеты входного и выходного сигналов и повышенная разрядность линий задержки не требуется. Однако в прямой структуре необходим сумматор повышенной разрядности.

Обращенная структура

Обращенная структура соответствует последовательному включению рекурсивной и нерекурсивной части. Один из вариантов обращенных структур (рисунок 3.1б) описывается следующими уравнениями и характеризуется использованием простых двухвходовых сумматоров:

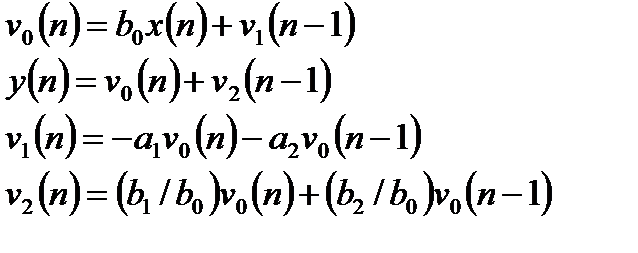. (3.2б)

Рисунок 3.1б – обращенная структура рекурсивного фильтра 2-го порядка

3.2.3.2. Канонические структуры ЛДС

Структуру ЛДС называют канонической, если число элементов задержки минимально и равно порядку передаточной функции.

Известно более 30 канонических структур ЛДС второго порядка, среди которых практическое применение нашли 2 структуры, характеризуемые минимальным количеством умножителей.

Каноническая структура 1

Эта структура основана на эквивалентном представлении передаточной функции в виде произведения:

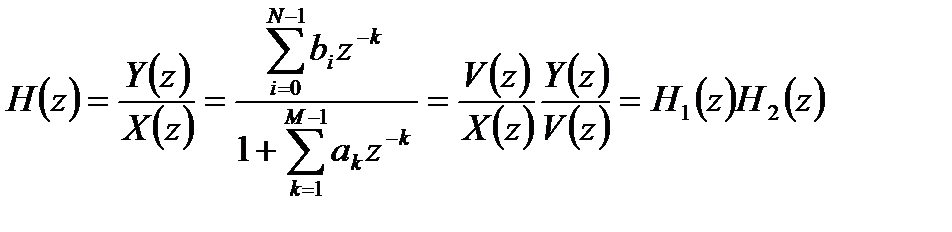, (3.3)

где ;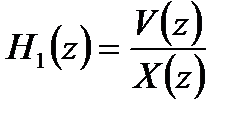

.

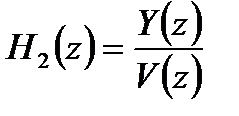Передаточным функциям 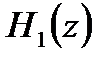и 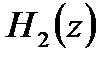соответст