Определение ускорений точек твёрдого тела

При плоском движении

Ускорения двух любых точек А и В плоской фигуры (твёрдого тела) связаны между собой зависимостью [1]:

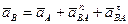, (39)

где 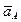– ускорение точки А (полюса);

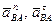– нормальное и касательное ускорения точки В при вращении фигуры вокруг полюса А.

При этом:

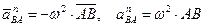; (40)

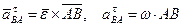, (41)

где w – угловая скорость тела,

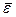– вектор углового ускорения тела, направленный перпендикулярно плоскости движения.

Вектор 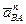всегда направлен от точки В к полюсу А,

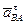– перпендикулярно отрезку АВ в сторону углового ускорения тела.

На рисунке 37 показана векторная зависимость (39), где введено обозначение 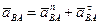– полное ускорение точки В при вращении фигуры вокруг полюса А.

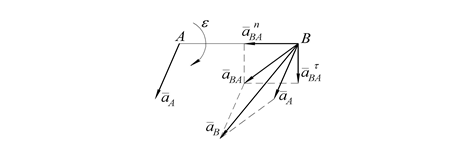
Рисунок 37 – Векторная зависимость

Таким образом, для определения ускорения произвольной точки В необходимо знать ускорение какой-либо другой точки А плоской фигуры, принимаемой за полюс, а также мгновенные угловую скорость w и угловое ускорение e фигуры. Тогда, складывая три вектора 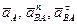(рис. 37), находим искомое ускорение точки В как сумму этих векторов.

Такой способ применим в случае, если угол поворота тела задан в виде функции о времени 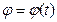, так как тогда можно определить 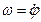и .

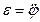Во многих задачах зависимость 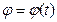неизвестна, и мгновенная угловая скорость w может быть найдена только для данного положения тела. В этом случае мгновенное угловое ускорение e тела не может быть найдено непосредственно.

Задачи на определение ускорений точек твёрдого тела, тем не менее, могут быть решены, если кроме известного ускорения полюса также будет известна траектория какой-либо другой точки тела (прямолинейная или криволинейная). Проецируя в этом случае равенство (39) на направление отрезка АВ, получаем уравнение с одним неизвестным 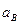(если траектория точки В прямолинейна) или 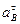(если траектория точки В криволинейна). При криволинейной траектории ускорение точки В раскладывается на нормальное и касательное ускорения, т.е.:

,

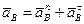где 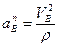(r – радиус кривизны траектории точки В).

Далее составляем второе уравнение проекций (39) на направление 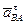, перпендикулярное к АВ. В этом уравнении будет одно неизвестное 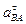, после определения которого находится угловое ускорение тела e в данный момент времени по формуле:

.

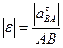В дальнейшем определение ускорений других точек тела также выполняется по формуле вида (39).

План решения задач

Тип I. Заданы скорость и ускорение одной точки плоской фигуры (или они легко находятся из условия задачи) и траектория другой точки фигуры. Требуется определить ускорения каких-либо точек фигуры.

1) Найти мгновенный центр скоростей тела и по заданной скорости точки тела и расстоянию от неё до МЦС по формуле (3.7) определить мгновенную угловую скорость w плоской фигуры. Если фигура совершает в данном положении мгновенно-поступательное движение, то w = 0.

2) Определить скорость точки тела (пусть точка В), заданная траектория которой криволинейна.

3) Найти нормальное ускорение точки В по формуле:

,

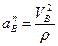где r – радиус кривизны траектории точки В.

При этом вектор 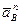направлен по нормали к траектории к центру кривизны.

4) Выбрать за полюс точку тела (например, точку А), ускорение которой известно или легко находится из условия задачи, и записать векторное выражение (39) для ускорения точки В, т.е.:

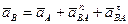. (42)

В случае криволинейных траекторий точек А и В, выражение (42) принимает вид:

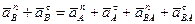. (43)

В векторных уравнениях (42) и (43) ускорения 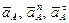известны или легко находятся из условия задачи; вектор 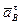направлен по касательной к траектории точки В, а вектор 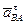– перпендикулярно отрезку АВ. Величины 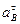, 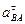– неизвестны.

5) Определить модуль нормального ускорения 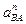точки В вокруг полюса А по формуле 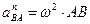. Вектор 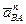направлен от точки В к точке А.

6) Спроецировать выражение (42) или (43) на направление отрезка АВ и из полученного уравнения найти ускорение 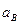или .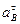

7) Спроецировать уравнение (42) или (43) на ось, перпендикулярную АВ (при этом величины ускорени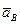й и 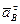уже будут известны) и из полученного уравнения определить ускорение .

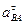8) Найти мгновенное угловое ускорение тела по формуле:

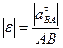. (44)

Направление углового ускорения определяется направлением вектора ускорения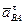

9) Определить при помощи формулы вида (42) ускорение любой точки плоской фигуры.

Тип II. Заданы ускорения двух точек плоской фигуры. Требуется определить мгновенные угловые скорость и ускорение тела, а также ускорение любой его точки.

Пример 3. Для плоского механизма, рассмотренного в примере 1, определить ускорения точек А, В и D, а также мгновенное угловое ускорение звена АВ, если угловое ускорение звена О₁А равно 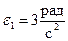(рис. 38).

Решение. Данная задача определения ускорений точек А, В и D стержня АВ, совершающего плоское движение, относится к задачам типа I, так как скорость и ускорение точки А, как точки вращающегося звена О₁А, легко находятся, а траектория точки В задана (прямолинейная направляющая ползуна).

1) Мгновенный центр скоростей и мгновенная угловая скорость звена АВ найдены в решении примера 1, т.е.:

.

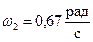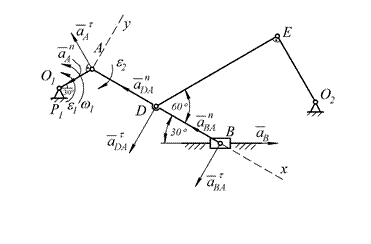
Рисунок 38 – К примеру 3

2) Определяем ускорение точки А, как точки звена О₁А, вращающегося вокруг точки О₁:

,

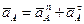где 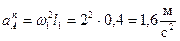– нормальное ускорение;

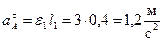– касательное ускорение;

векторы 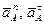показаны на рисунке 38.

Величина ускорения равна:

.

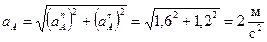3) Принимаем за полюс точку А и записываем векторное выражение для ускорения точки В:

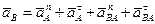, (45)

где 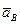– направлено по направляющей ползуна предположительно вправо;

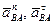– нормальное и касательное ускорения точки В вокруг полюса А (рис. 38).

4) Определяем нормальное ускорение точки В вокруг полюса А:

.

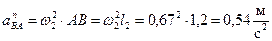5) Спроецируем выражение (3.17) на ось x, направленную по отрезку АВ (рис.3. 11):

.

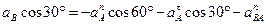Отсюда находим ускорение точки В:

.

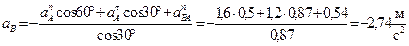Знак "–" указывает на то, что вектор ускорения точки В в действительности направлен влево.

6) Спроецируем уравнение (45) на ось y, перпендикулярную АВ (рис. 38):

.

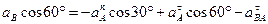Из полученного уравнения определяем ускорение :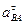

.

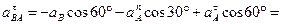
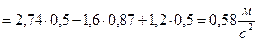Знак "+" показывает, что вектор 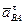в действительности направлен, как показано на рисунке 38.

7) Находим мгновенное угловое ускорение звена АВ по формуле (44):

.

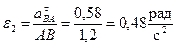Угловое ускорение 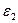направленно соответственно ускорению 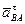, т.е. по часовой стрелке (рис. 38).

8) Определяем ускорение точки D в соответствии с формулой:

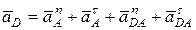, (46)

где величины 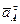и 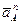найдены выше,

, .

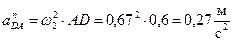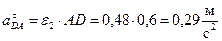Вектор 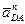направлен от D к А, а вектор 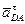– перпендикулярно АD в соответствии с направлением углового ускорения e₂ (рис. 38).

Спроецируем выражение (46) на оси x и y (рис. 38), т.е. найдём проекции ускорения точки D на эти оси:

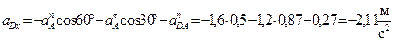
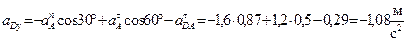
Вычисляем модуль ускорения точки D:

.

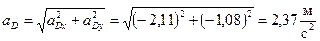Находим направляющие косинусы:

;

.

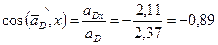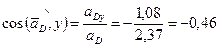Ответ: .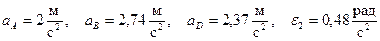

Сложное движение точки