Периодические функции и их свойства

О п р е д е л е н и е 1. Функция 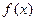называется в области 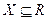периодической функцией с периодом Т (или Т– периодической функцией), если существует такое положительное число Т, при котором 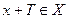и

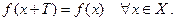(1)

Наименьшее из чисел Т, при которых выполнено условие (1), называется главным периодом функции .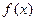

О п р е д е л е н и е 2.Процессы, описываемые периодическими с периодом 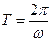функциями

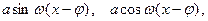(2)

где 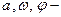постоянные числа и 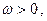называют гармоническими колебаниями. При этом называют:

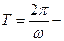периодом колебаний, 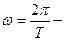круговой частотой колебаний,

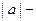амплитудой колебаний, 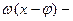фазой колебаний,

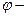начальной фазой (или сдвигом фазы).

Свойства 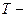периодических функций

С в о й с т в о 1.Линейная комбинация любого конечного числа 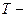периодических функций есть периодическая функция периода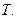

С в о й с т в о 2.Для любой 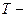периодической на 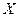функции 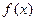справедливо равенство:

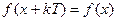, (3)

где 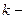целое число, такое, что .

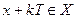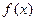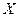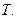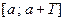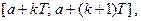С в о й с т в о 3.Пусть функция является в области периодической с периодом Тогда ее график на любых отрезках и где 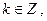целиком лежащих в 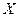и имеющих длину периода 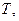связаны параллельным переносом на вектор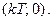

С в о й с т в о 4. Пусть функция 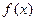является в области 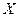периодической с периодом 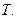Тогда справедливо равенство:

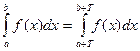(4)

при любых числах 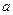и 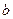таких, что ,

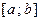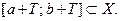
С в о й с т в о 5. Пусть функция 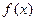является в области 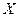периодической с периодом 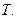Тогда справедливо равенство:

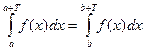(5)

при любых числах 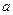и 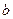таких, что ,

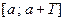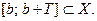
С л е д с т в и е.Пусть функция 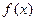является в области 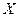периодической с периодом 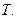Тогда справедливы равенства:

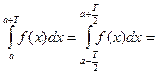
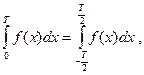
если ,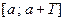

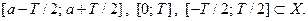
2. ОРТОГОНАЛЬНАЯ СИСТЕМА ФУНКЦИЙ

О п р е д е л е н и е 3.Система функций

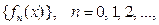
называется ортогональной на отрезке 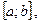если выполнены условия:

,

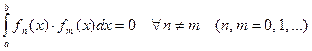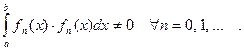
О п р е д е л е н и е 4.Система функций

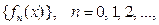
называется ортонормированной на отрезке 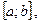если она ортогональная и выполнено условие: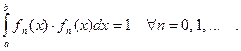

Т е о р е м а 1. Система тригонометрических функций

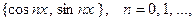(6)

является ортогональной на любом отрезке длины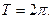

З а м е ч а н и е 2.Система функций

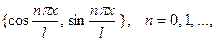(7)

где 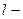некоторое положительное число, является ортогональной на любом отрезке длины 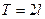. При этом справедливы равенства:

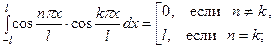
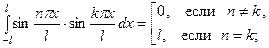
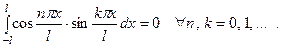
З а м е ч а н и е 3.Система функций

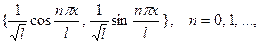(8)

где 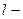некоторое положительное число, является ортонормированной на любом отрезке длины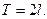

3. ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ

О п р е д е л е н и е 5.Функциональный ряд вида

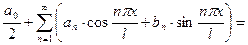
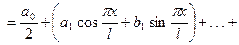
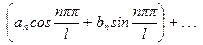(9)

называется тригонометрическим рядом. Числа 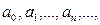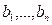,… называются коэффициентами тригонометрического ряда (9).

З а м е ч а н и е 4. Так как любая из функций 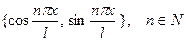, является 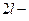периодической, то частичная сумма 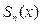ряда (9) также будет 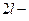периодической функцией. Следовательно, если ряд (9) сходится, то есть существует предел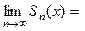 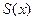, то сумма 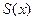ряда (9) является 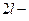периодической функцией.

Т е о р е м а 1.Пусть тригонометрический ряд (9) сходится и его сумма равна 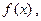то есть имеет место представление

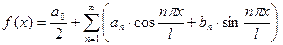, (10)

допускающее почленное интегрирование на отрезке 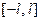. Тогда числа 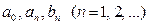связаны с функцией 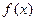по формулам:

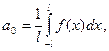
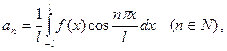(11)

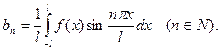(12)