Функциональные последовательности

О п р е д е л е н и е 1. Функциональной последовательностью называется бесконечная последовательность

(1)

элементами которой являются функции одной и той же переменной 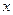, определенные на общей области

О п р е д е л е н и е 2. Если при любом ф и к с и р о в а н н о м существует конечный предел

, (2)

то есть

, (3)

то функция 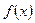называется предельной функцией для функциональной последовательности (1).

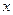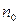З а м е ч а н и е 1.Предел (2) представляет собой функцию переменной , определенную на области . В формуле (3) номер существенно зависит от и меняется при переходе от одного значения 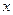к другому, принимая в общем случае бесконечное множество значений.

Поэтому естественно встает следующий вопрос: существует ли такой номер 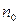, который при заданном числе будет пригодным для в с е х . Ответ на поставленный вопрос, оказывается, может быть и «да», и «нет» в зависимости от рассматриваемых функций (1).

О п р е д е л е н и е 3. Говорят, что функциональная последовательность (1) сходится равномерно в области к своей предельной функции 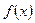(пишут ), если существует предел (2) и выполняется условие:

(4)

Если предел (2) существует, но условие (4) не выполнено, то говорят, что последовательность (1) сходится неравномерно в области (или просто сходится) к функции .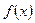

Пишут:

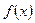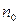Т е о р е м а 1 (условие равномерной сходимости функциональной последовательности). Для того чтобы последовательность (1) имела предельную функцию и сходилась к ней равномерно в области , необходимо и достаточно, чтобы для любого сколь угодно малого числа нашелся такой номер , зависящий от 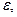что для всех и при любом натуральном числе выполнялось неравенство:

2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ. ОБЛАСТЬ СХОДИМОСТИ

О п р е д е л е н и е 4. Выражение вида

, (5)

где некоторая последовательность функций переменной 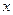, определенных в области , называется функциональным рядом и условно обозначается символом:

З а м е ч а н и е 2.При каждом фиксированном функциональный ряд (5) превращается в числовой ряд

,

который, может оказаться, при одних 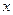сходится, при других – расходится.

О п р е д е л е н и е 5.Функция вида

(6)

называется й частичной суммой ряда (5).

О п р е д е л е н и е 6. Говорят, что ряд (5) сходится в точке , если существует конечный предел

(7)

называемый суммой ряда (5) в точке .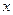

О п р е д е л е н и е 7.Остатком порядка ряда (5) в точке 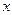называется функция вида

(8)

З а м е ч а н и е 3. Справедливо следующее свойство: если ряд (5) сходится в точке 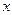к числу то при 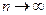остаток ряда стремится к нулю в точке 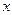, то есть

О п р е д е л е н и е 8.Множество 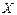всех точек при которых ряд (5) сходится, называется областью сходимостиряда (5).

З а м е ч а н и е 4. В частных случаях область сходимости функционального ряда может быть пустым множеством, может принадлежать или может совпадать с .

З а м е ч а н и е 5. Области определения функци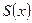й и вида (7) и (8) совпадают с областью сходимости ряда (5).