Случайные события и действия над ними. Виды случайных событий. Комбинации событий Пространство элементарных событий.

Случайные события и действия над ними. Виды случайных событий. Комбинации событий Пространство элементарных событий.

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.

Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:

а) достоверное событие – событие, которое всегда происходит при проведении опыта;

б) невозможное событие – событие, которое в результате опыта произойти не может;

в) случайное событие – событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков.

Алгебра событий.

1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.

Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В (рис. 1).

2. Произведением АВсобытий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.

Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В.

3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.

Введем еще несколько категорий событий.

4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.

Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием.

5. Говорят, что события А₁, А₂,…,А_п образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.

Замечание. В частности, если события, образующие полную группу, попарно несовмест-ны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.

6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.

Вероятность событий

При изучении случайных событий возникает необходимость количественно сравнивать возможность их появления в результате опыта. Например, при последовательном извлечении из колоды пяти карт более возможна ситуация, когда появились карты разных мастей, чем появление пяти карт одной масти; при десяти бросках монеты более возможно чередование гербов и цифр, нежели выпадение подряд десяти гербов, и т.д. Поэтому с каждым таким событием связывают по определенному правилу некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события и является вторым основным понятием теории вероятностей.

Отметим, что само понятие вероятности, как и понятие случайного события, является аксиоматическим и поэтому не поддается строгому определению. То, что в дальнейшем будет называться различными определениями вероятности, представляет собой способы вычисления этой величины.

Если все события, которые могут произойти в результате данного опыта,

а) попарно несовместны;

б) равновозможны;

в) образуют полную группу,

то говорят, что имеет место схема случаев.

Можно считать, что случаи представляют собой все множество исходов опыта. Пусть их число равно п ( число возможных исходов), а при т из них происходит некоторое событие А (число благоприятных исходов).

Вероятностью события Аназывается отношение числа исходов опыта, благоприятных этому событию, к числу возможных исходов:

- классическое определение вероятности.

Свойства вероятности.

Из определения 1.8 вытекают следующие свойства вероятности:

1. Вероятность достоверного события равна единице.

Доказательство. Так как достоверное событие всегда происходит в результате опыта, то все исходы этого опыта являются для него благоприятными, то есть т = п, следовательно,

Р(А) = 1.

2. Вероятность невозможного события равна нулю.

Доказательство. Для невозможного события ни один исход опыта не является благопри-ятным, поэтому т = 0 и р(А) = 0.

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Доказательство. Случайное событие происходит при некоторых исходах опыта, но не при всех, следовательно, 0 < m < n, и из (1.1) следует, что 0 < p(A) < 1.

Геометрическая вероятность

Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности.

Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка L не зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошен-ная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле:

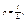(2.1)

где l – длина отрезка l, а L – длина отрезка L.Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s:

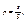(2.1`)

где s – площадь части области, а S – площадь всей области.

В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его часть v, задается формулой:

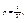(2.1``)

где v – объем части тела, а V – объем всего тела.

3.Теоремы теории вероятностей. Теорема сложения вероятностей несовместимых событий. Полная группа событий. Противоположные события.

Теорема1. (теорема сложения).Вероятность р(А + В) суммы событий А и В равна

Р (А + В ) = р (А) + р (В) – р (АВ). (2.2)

Доказательство.

Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, т_А – число исходов, благоприятных событию А, т_В – число исходов, благопри-ятных событию В, а т_АВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно т_А + т_В – т_АВ (так как в сумме (т_А + т_В) т_АВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):

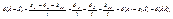
что и требовалось доказать.

Теорему1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С

Р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС)

Теорема 2. Сумма вероятностей противоположных событий равна 1:

р(А) + р( 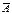) = 1. Доказательство.

Так как А и 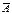образуют полную группу, то одно из них обязательно произойдет в результате опыта, то есть событие А + 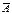является достоверным. Следовательно,

Р( А + 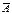) = 1. Но, так как А и 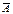несовместны, из (2.4) следует, что Р(А + 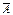) = р(А) + р( 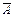). Значит, р(А) + р( 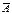) = 1, что и требовалось доказать.

Замечание. В ряде задач проще искать не вероятность заданного события, а вероятность события, противоположного ему, а затем найти требуемую вероятность по формуле (2.5).

Другие виды распределений

Биномиальное распределение.

Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний (см. лекцию 6), М(Х) можно найти, используя свойство 4 математического ожидания. Пусть Х₁ – число появлений А в первом испытании, Х₂ – во втором и т.д. При этом каждая из случайных величин Х_i задается рядом распределения вида

Xi
pi	q	p

Следовательно, М(Х_i) = p. Тогда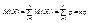

Аналогичным образом вычислим дисперсию: D(X_i) = 0²·q + 1²·p – p²= p – p² = p(1 – p), откуда по свойству 4 дисперсии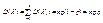

Неравенство Чебышева.

Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.

Неравенство Чебышева.

p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)

Доказательство. Пусть Х задается рядом распределения

Х	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x₁ – M(X))²p₁ + (x₂ – M(X))²p₂ + … + (x_n – M(X))²p_n . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

D(X) ≥ (x_k+1 – M(X))²p_k+1 + (x_k+2 – M(X))²p_k+2 + … + (x_n – M(X))²p_n ≥ ε² (p_k+1 + p_k+2 + … + p_n).

Отметим, что p_k+1 + p_k+2 + … + p_n есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.

Теорема Бернулли.

теорема Бернулл. Если в каждом из п независимых опытов вероятность р появления события А постоянна, то при достаточно большом числе испытаний вероят-ность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к

1: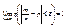

Доказательство. Введем случайные величины Х₁, Х₂, …, Х_п, где X_i – число появлений А в i-м опыте. При этом X_i могут принимать только два значения: 1(с вероятностью р) и 0 (с вероятностью q = 1 – p). Кроме того, рассматриваемые случайные величины попарно независимы и их дисперсии равномерно ограничены (так как D(X_i) = pq, p + q = 1, откуда pq ≤ ¼ ). Следовательно, к ним можно применить теорему Чебышева при M_i = p:

.

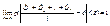Но 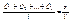, так как X_i принимает значение, равное 1, при появлении А в данном опыте, и значение, равное 0, если А не произошло. Таким образом,

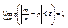
что и требовалось доказать.

Замечание. Из теоремы Бернулли не следует, что 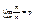Речь идет лишь о вероятно-сти того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство 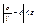выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.

Системы случайных величин. Закон распределения вероятностей дискретной двумерной случайной величины. Функции распределения двумерной случайной величины и ее свойства. Двумерная плотность вероятности и ее свойства.

Закон распределения дискретной двумерной случайной величины (Х, Y)имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(x_i, y_j), с которыми величина принимает значение (x_i, y_j):

Y	Х
x1	x2	…	xi	…	xn
y1	p(x1, y1)	p(x2, y1)	…	p(xi, y1)	…	p(xn, y1)
…	…	…	…	…	…	…
yj	p(x1, yj)	p(x2, yj)	…	p(xi, yj)	…	p(xn, yj)
…	…	…	…	…	…	…
ym	p(x1, ym)	p(x2, ym)	…	p(xi, ym)	…	p(xn, ym)

При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.

Зная закон распределения двумерной случайной величины, можно найти законы распреде-ления ее составляющих. Действительно, событие Х = х₁ представляется собой сумму несовместных событий (X = x₁, Y = y₁), (X = x₁, Y = y₂),…, (X = x₁, Y = y_m), поэтому

р(Х = х₁) = p(x₁, y₁) + p(x₁, y₂) +…+ p(x₁, y_m) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х₁). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = y_j.

Функцией распределения F(x, y)двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y: F( х, у ) = p ( X < x, Y < y ). (8.1)

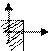Рис.1. Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у). Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины. Свойства функции распределения. 1)0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью). 2)F(x, y) есть неубывающая функция по каждому аргументу: F(x₂, y) ≥ F(x₁, y), если x₂ > x F(x, y₂) ≥ F(x, y₁), если y₂ > y₁. Доказательство. F(x₂, y) = p(X < x₂, Y < y) = p(X < x₁, Y < y) + p(x₁ ≤ X < x₂, Y < y) ≥ p(X < x₁, Y < y) = F(x₁, y). Аналогично доказывается и второе утверждение. 3)Имеют место предельные соотношения: а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1. Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств. 4)При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х: F(x, ∞) = F₁(x). При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y : F( ∞, y) = F₂(y). Доказательство. Так как событие Y < ∞ достоверно, то F(x, ∞) = р(Х < x) = F₁(x). Аналогично доказывается второе утверждение. Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности)непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения 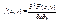. (8.2) Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при 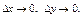Свойства двумерной плотности вероятности.

1)f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен). 2) 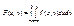(cледует из определения двумерной плотности вероятно-сти). 3) 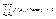(поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события).

Случайные события и действия над ними. Виды случайных событий. Комбинации событий Пространство элементарных событий.

В различных разделах науки и техники нередко возникают ситуации, когда результат каждого из многих проводимых опытов заранее предугадать невозможно, однако можно исследовать закономерности, возникающие при проведении серии опытов. Нельзя, напри-мер, точно сказать, какая сторона монеты окажется сверху при данном броске: герб или цифра – но при большом количестве бросков число выпадений герба приближается к по-ловине количества бросков; нельзя заранее предсказать результат одного выстрела из дан-ного орудия по данной цели, но при большом числе выстрелов частота попадания прибли-жается к некоторому постоянному числу. Исследование вероятностных закономерностей массовых однородных явлений составляет предмет теории вероятностей.

Основным интуитивным понятием классической теории вероятностей является случайное событие. События, которые могут произойти в результате опыта, можно подразделить на три вида:

а) достоверное событие – событие, которое всегда происходит при проведении опыта;

б) невозможное событие – событие, которое в результате опыта произойти не может;

в) случайное событие – событие, которое может либо произойти, либо не произойти. Например, при броске игральной кости достоверным событием является выпадение числа очков, не превышающего 6, невозможным – выпадение 10 очков, а случайным – выпадение 3 очков.

Алгебра событий.

1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответ-ственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.

Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В (рис. 1).

2. Произведением АВсобытий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.

Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В.

3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет.

Введем еще несколько категорий событий.

4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными.

Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек.

Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием.

5. Говорят, что события А₁, А₂,…,А_п образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы.

Замечание. В частности, если события, образующие полную группу, попарно несовмест-ны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями.

6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое.