Кафедра электроэнергетики и электротехники
МОДЕЛИРОВАНИЕ ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ
Методические указания
Санкт-Петербург
УДК 658.382.3:621.3
Рецензент канд. техн. наук, доц. Соколов В.Я.(СПбГАСУ)
Моделирование электрических цепей: метод.указ./ сост. В.В. Резниченко, О.П. Томчина; СПбГАСУ. – СПб., 2014 – с. 25
Методические указания к выполнению курсовой работы по моделированию электрических цепей для студентов специальности 140.000 «Электроэнергетика и электротехника».
Предназначены для выполнения курсовой работы по общей электротехнике, целью которой является закрепление знаний об основных методах расчета линейных цепей во временной и частотной областях.
Указания включают краткое изложение вопросов теории и пояснение к оформлению работы.
Табл. 1. Ил. 11. Библиограф. 8
Ó Санкт-Петербургский государственный
архитектурно-строительный университет, 2014
ЦЕЛЬ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
Целью данной курсовой работы является закрепление и углубление знаний, полученных на лекциях, практических и лабораторных занятиях по курсу «Общей электротехники», а также приобретение необходимых навыков и опыта при самостоятельном освоении различных методов количественного и качественного анализа процессов передачи сигналов через линейные электрические цепи.
Расчет начинается с нахождения входной и передаточной функций заданной цепи. Затем определяются переходная и импульсная характеристики для выходного сигнала. Реакция на выходе цепи находится также:
а) при воздействии сигнала в виде одиночного импульса;
б) при периодическом несинусоидальном режиме.
Для использования вычислительных средств в курсовой работе введен раздел о формировании описания заданной электрической цепи по методу пространства состояний.
В целом с учетом содержания курса «Общей электротехники и электроники» и специфики последующих дисциплин, изучаемых студентами специальности 2203, материал курсовой работы охватывает следующие разделы теории цепей: анализ линейных электрических цепей во временной области; переходные и импульсные характеристики схемы; анализ цепей при установившемся гармоническом режиме методом комплексных амплитуд; теория четырехполюсников; методы расчета сложных цепей; использование операторного и частотных методов анализа.
Задание к курсовой работе
В курсовой работе исследуется цепь второго порядка с наиболее распространенной лестничной структурой. Для заданной цепи находятся входная и передаточная функции, и затем определяются переходная и импульсная характеристики для выходного сигнала. Формируются уравнения цепи через переменные состояния. Определятся спектр входного воздействия и его ширина и частотная характеристика цепи. После этого определяется спектр реакции цепи на единичное воздействия. Реакция цепи находится:
а) при воздействии сигнала в виде одиночного импульса;
б) при периодическом несинусоидальном режиме.
Задание. Резистивная нагрузка R = 1 Ом соединена с источником при помощи пассивного линейного четырехполюсника, представляющего собой цепь типа RL, RC или RLC. Возможные схемы цепей показаны на рис. 1 и 2. В табл. 1 указаны параметры схем, форма и длительность одиночного импульса для одного из вариантов расчета. Формы импульсов представлены 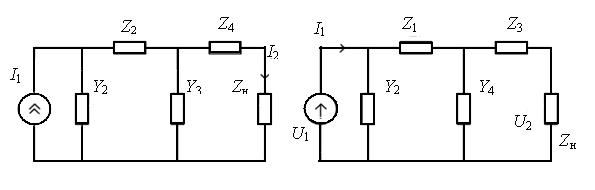
Рис. 1 Рис. 2
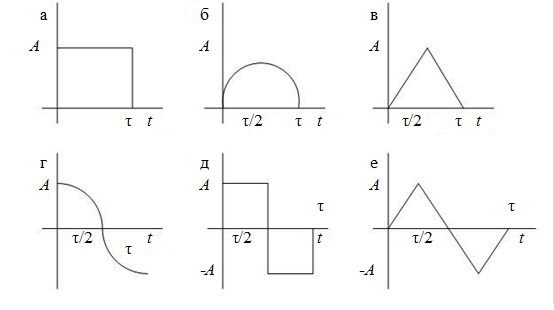
Рис.3
| Вариант | Характеристики элементов | Характеристики сигналов | ||||||
| Форма Рис.3 | t, с | Амплитуда, | n=T, t | |||||
| Схема рис.1 | ||||||||
| L = 4 | R = 1 | L = 2 | R = 2 | а | 0.1 | |||
| R = 1 | L = 4 | R = 2 | L = 1 | е | ||||
| L = 2 | R = 2 | R = 1 | L = 1 | в | ||||
| R = 2 | L = 1 | L = 4 | R= 2 | г | ||||
| R = 2 | R = 1 | L = 1 | L = 2 | д | ||||
| C = 1 | R = 1 | C = 3 | R = 2 | а | ||||
| R = 1 | C = 4 | R = 2 | C = 1 | б | ||||
| C = 3 | R = 1 | R = 2 | C = 1 | в | ||||
| R = 4 | C = 0.5 | C = 1 | R = 1 | е | ||||
| R = 0.5 | R = 0.5 | C = 2 | C = 0.5 | д | ||||
| L = 0.5 | R = 1 | C = 2 | R = 1 | а | ||||
| R = 0.5 | L = 2 | R = 2 | R = 2 | б | ||||
| L = 0.5 | R = 2 | R = 2 | C = 1 | в | 0.5 | |||
| C = 4 | R = 1 | C = 1 | R = 0.5 | д | 0.1 | |||
| R = 1 | L = 4 | R = 0.5 | C = 1 | а | ||||
| C = 2 | R = 0.5 | R = 1 | C = 1 | г | ||||
| R = 0.5 | C = 1 | C = 4 | R = 0.5 | в | ||||
| R = 0.5 | R = 1 | C = 2 | C = 1 | а | ||||
| L = I | R = 1 | L = 2 | R = 0.5 | е | ||||
| R = I | L = 4 | R = 0.5 | L = 1 | в | 0.5 | |||
| L = 3 | R = 1 | R = 0.5 | L = 1 | а | ||||
| R = 0.25 | L = 2 | L = 1 | R = 1 | е | ||||
| R = 0.25 | R = 1 | L = 1 | L = 2 | в | ||||
| C = 2 | R = 1 | L = 2 | R = 0.25 | д | ||||
| R = 1 | C = 4 | R = 0.2 | L = 2 | в | ||||
| C = 2 | R = 1 | R = 0.2 | L = 4 | г | 0.5 |
L – Гн; С – Ф; R – Oм.
