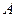Свойства операции умножения вектора на число
1. 1×  =
=  , -1×
, -1×  = -
= -  .
.
2. a×(b×  ) = (a×b)×
) = (a×b)×  .
.
3. a×(  +
+  ) = a×
) = a×  + a×
+ a×  .
.
4. (a + b)×  = a×
= a×  + b×
+ b×  .
.
Для доказательства свойств воспользуемся простым фактом: два вектора равны, если равны их длины и они сонаправлены.
Доказательство свойства1. 1). Если  =
= 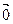 , то по определению операции умножения вектора на число получим, что правый вектор и левый вектор нулевые. Следовательно, равенство верно.
, то по определению операции умножения вектора на число получим, что правый вектор и левый вектор нулевые. Следовательно, равенство верно.
2). Покажем, что 1×  =
=  . Рассмотрим вектор 1×
. Рассмотрим вектор 1×  . Его длина, согласно определению 1, равна |1×
. Его длина, согласно определению 1, равна |1×  | = |1| ×|
| = |1| ×|  | = |
| = |  |. С другой стороны, длина вектора
|. С другой стороны, длина вектора  так же равна |
так же равна |  |. Следовательно, длины рассматриваемых векторов равны. Так как мы умножаем вектор
|. Следовательно, длины рассматриваемых векторов равны. Так как мы умножаем вектор  на положительное число 1, то 1×
на положительное число 1, то 1× 
 . Рассматриваемые вектора 1×
. Рассматриваемые вектора 1×  и
и  имеют одинаковую длину и одно направление. Следовательно, они равны. Вторая часть свойства 1 также верна, так как длины рассматриваемых векторов равны |-1×
имеют одинаковую длину и одно направление. Следовательно, они равны. Вторая часть свойства 1 также верна, так как длины рассматриваемых векторов равны |-1×  | = |-1| ×|
| = |-1| ×|  | = |
| = |  | и |-
| и |-  |= |
|= |  |, и их направления одинаковы: -1×
|, и их направления одинаковы: -1×  ¯
¯  , -
, -  ¯
¯  - то есть, они противоположно направлены одному и тому же вектору.
- то есть, они противоположно направлены одному и тому же вектору.
Свойство 1 доказано.
Доказательство свойства 2. Покажем, что a×(b×  ) = (a×b)×
) = (a×b)×  . (1)
. (1)
Для этого рассмотрим несколько случаев. 1). Пусть одно из чисел a или b равно нулю. Тогда по определению операции умножения вектора на число получаем, что и левый вектор и правый вектор равны нулевому вектору, то есть равенство (1) верно. Аналогично, если  =
= 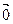 , то равенство (1) также верно.
, то равенство (1) также верно.
2). Пусть числа a и b - одного знака. Например, они отрицательные. Тогда b×  ¯
¯  , a×(b×
, a×(b×  ) ¯ b×
) ¯ b×  . Следовательно, a×(b×
. Следовательно, a×(b×  )
)  .
.
С другой стороны, (a×b)× 
 , так как a×b > 0.
, так как a×b > 0.
Таким образом, a×(b×  ) (a×b)×
) (a×b)×  .
.
Для длин рассматриваемых векторов, независимо от знаков рассматриваемых чисел a и b, в силу определения операции умножения вектора на число, имеем:
|a×(b×  )| = |a|×|(b×
)| = |a|×|(b×  )| = |a|×|b|×|
)| = |a|×|b|×|  |,
|,
|(a×b)×  | = |a×b|×|
| = |a×b|×|  | = |a|×|b|×|
| = |a|×|b|×|  |.
|.
Таким образом, рассматриваемые векторы имеют одинаковую длину и одинаковое направление. Следовательно, равенство (1) верно.
Аналогично рассмотреть случай, когда числа a и b - положительные.
3). Пусть числа a и b - разного знака. Например, a > 0 , b < 0. Тогда
b×  ¯
¯  , a×(b×
, a×(b×  ) b×
) b×  . Следовательно, a×(b×
. Следовательно, a×(b×  )¯
)¯  .
.
С другой стороны, (a×b)×  ¯
¯  , так как a×b < 0.
, так как a×b < 0.
Таким образом, a×(b×  ) (a×b)×
) (a×b)×  .
.
Аналогично рассмотреть случай, когда числа a < 0 и b > 0.
Таким образом, рассматриваемые векторы имеют одинаковую длину и одинаковое направление. Следовательно, равенство (1) верно и в этом случае. Свойство 2 доказано.
Доказательство свойства 3: a×(  +
+  ) = a×
) = a×  + a×
+ a×  . Если a = 0 или хотя бы один из векторов нулевой, то свойство (3), очевидно, выполняется. Поэтому рассматриваем ненулевые варианты. Выберем произвольно точку О и от нее откладываем вектор
. Если a = 0 или хотя бы один из векторов нулевой, то свойство (3), очевидно, выполняется. Поэтому рассматриваем ненулевые варианты. Выберем произвольно точку О и от нее откладываем вектор 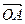 =
=  , а от точки А откладываем вектор
, а от точки А откладываем вектор 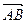 =
=  . При этом получили
. При этом получили 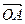 +
+ 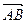 =
= 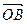 . Итак,
. Итак, 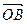 =
=  +
+  . Рассмотрим гомотетию с центром О и коэффициентом a. Пока считаем, что a > 0.
. Рассмотрим гомотетию с центром О и коэффициентом a. Пока считаем, что a > 0.
Пусть при рассматриваемой гомотетии: 
Тогда треугольники ОАВ и ОА`В` имеют попарно параллельные стороны.


При этом  = a
= a  ,
,  = a
= a  ,
,  = a
= a 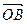 = a (
= a (  +
+  ) и
) и  +
+  =
=  . Отсюда получаем равенство
. Отсюда получаем равенство
a×(  +
+  ) = a×
) = a×  + a×
+ a×  .
.
Если a < 0, то сначала рассмотрим равенство
|a|×(  +
+  ) = |a|×
) = |a|×  +| a|×
+| a|×  ,
,
а затем умножив обе части этого равенства на ( - 1), получим:
-|a|×(  +
+  ) = -|a|×
) = -|a|×  -| a|×
-| a|× 
или
a×(  +
+  ) = a×
) = a×  + a×
+ a×  .
.
Свойство 3 доказано.
Доказательство свойства 4: (a + b)×  = a×
= a×  + b×
+ b×  .
.
Доказательство распадается на несколько отдельных случаев. 1) a > 0 и b > 0. В этом случае a×  b×
b×  и равенство (a + b)×
и равенство (a + b)×  = a×
= a×  + b×
+ b×  - верно.
- верно.
2) Если a < 0 и b < 0, то, в силу первого случая, будет верным следующее равенство
(|a| + |b|)×  =|a|×
=|a|×  + |b|×
+ |b|×  .
.
Умножая это равенство на (-1) получим равенство
(-|a|- |b|)×  = - |a|×
= - |a|×  - |b|×
- |b|×  ,
,
а, следовательно, и равенство
(a + b)×  =a×
=a×  + b×
+ b×  .
.
3) Здесь мы должны рассмотреть случай, когда a и b разных знаков. При этом можно считать, что a > 0, а b < 0. Но мы должны учесть два различных случая: a > |b| и a < |b| .
Рассмотрим, например, случай a > |b|. Тогда a + b > 0. Очевидно числовое равенство a + b + |b| = a. Согласно первому случаю, выполняется равенство
((a + b)+|b|) ×  = (a + b)×
= (a + b)×  + |b|×
+ |b|× 
или
a ×  = (a + b)×
= (a + b)×  + |b|×
+ |b|×  .
.
Отсюда получим
(a + b)×  = a×
= a×  − |b|×
− |b|×  ,
,
а, следовательно, и равенство
(a + b)×  = a×
= a×  + b×
+ b×  .
.
Аналогично рассматривается случай a < |b|.
Свойство 4 доказано.
Пример 1. Дан треугольник АВС и произвольная точка О пространства. М – точка пересечения медиан треугольника АВС (ее называют центром тяжести треугольника). Доказать, что  .
.
Доказательство. Рассмотрим медиану АК треугольника АВС. 

Тогда, в силу свойств медианы имеем:  . С другой стороны,
. С другой стороны,

 ,
,
 ,
,  ,
,  .
.
Следовательно,  .
.
Находим: 
 (
(  .
.

 .
.
Пример 2.В трапеции АВСD с основаниями ВС и AD точки M и N являются серединами оснований, точка О – точка пересечения прямых, содержащих боковые стороны. Доказать, что точки О, М, N лежат на одной прямой.
Решение. Рассмотрим векторы  и
и  . Для того , чтобы доказать, что точки О, М, N лежат на одной прямой достаточно доказать, что
. Для того , чтобы доказать, что точки О, М, N лежат на одной прямой достаточно доказать, что  ||
||  .
.
|





|
|
|


 (1),
(1),
|

|
 (2).
(2).
|
 и
и  с коэффициентом подобия k следует, что
с коэффициентом подобия k следует, что  (3) и
(3) и  (4).
(4).
Из равенств (2), (3) и (4) получаем следующее равенство:
 . Следовательно,
. Следовательно,  , откуда
, откуда  , а это означает, что точки O, M, N лежат на одной прямой.
, а это означает, что точки O, M, N лежат на одной прямой.