Как и в школьном курсе геометрии, мы будем называть фигурой любое множество точек. Точки будем обозначать большими латинскими буквами, прямые – малыми латинскими буквами, а плоскости, в основном, – малыми буквами греческого алфавита. Если прямая задана точками А и В, то ее будем обозначать (А,В). Отрезок с концами А и В будем обозначать [A,B], а луч с началом в точке А и промежуточной точкой В - [А,В). Длину отрезка c концами А и В будем обозначать |AB|. Параллельные прямые 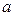 и
и 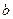 обозначаем:
обозначаем: 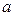 ||
|| 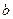 .
.
В школьном курсе геометрии параллельными прямыми называются прямые, лежащие в одной плоскости и при этом не пересекающиеся. Лучи [А,В) и [С,D) называются параллельными, если они лежат на параллельных прямых. Прямая (А,В) называется параллельной плоскости α, если они не пересекаются. Луч [А,В) называется параллельным плоскости α, если плоскость α и прямая (А,В) параллельны. Если два луча [А,В) и [С,D) параллельны, то они имеют либо одно направление, либо противоположные направления.
Определение 1. Параллельные лучи [А,В) и [С,D), лежащие на разных прямых (А,В) и (С,D) называются сонаправленными, если они лежат в одной полуплоскости с границей (А,С). Лучи [А,В) и [С,D), лежащие на одной прямой (А,В) называются сонаправленными, если их пересечением является луч.




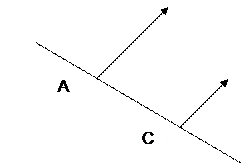
Определение 2. Параллельные лучи [А, В) и [С, D), которые не являются сонаправленными, называются противоположно направленными.


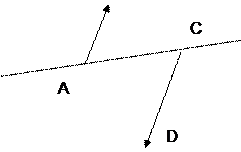

Обозначаем сонаправленные лучи: [А,В) [С,D), а противоположно направленные лучи: [А,В) ¯ [С,D).
Теорема 1. Свойство лучей быть сонаправленными является свойством эквивалентности, то есть это свойство лучей рефлексивно, симметрично и транзитивно.
Доказательство. Докажем свойство рефлексивности: [А,В)[А,В). Так как луч [А,В) лежит на одной прямой сам с собой и пересечение [А,В) Ç[А,В) = [А,В), то согласно определению луч [А,В) сам себе сонаправлен, то есть, свойство рефлексивности доказано.
Докажем свойство симметричности:если [А,В)[С,D), то [С,D) [А,В). Так как [А,В) [С,D), то лучи [А,В) и [С,D) лежат либо на одной прямой и их пересечение есть луч, но тогда и лучи [С,D) и [А,В) лежат на одной прямой и их пересечение есть луч, то есть [С,D) [А,В), либо лежат на разных параллельных прямых (А,В) и (С,D) в одной полуплоскости с границей (А,С). Тогда и лучи [С,D) и [А,В) так же лежат на разных параллельных прямых (С,D) и (А,В) в одной полуплоскости с границей (А,С). Следовательно, [С,D) [А,В), свойство симметричности доказано.
Докажем свойство транзитивности. Пусть даны три луча, при этом [А,В) [С,D), [С,D) [Е,F). Если хотя бы одна пара лучей лежит на одной прямой, то, очевидно свойство транзитивности выполняется. Поэтому будем считать, что лучи лежат на разных прямых, при этом точки А, С и Е определяют единственную плоскость α, относительно которой все лучи лежат в одном полупространстве, а, следовательно, лучи [А,В) и [Е,F) лежат в одной полуплоскости определяемой прямой (Е,F). Учитывая, что параллельность прямых обладает свойством транзитивности, получим параллельность лучей [А,В) и [Е,F).
Теорема доказана.
Как известно, свойство эквивалентности разбивает рассматриваемое множество на классы эквивалентности.
Определение 3. Отношение сонаправленности лучей пространства разбивает все лучи пространства на классы, каждый из которых мы называем направлением в пространстве.
Определение 4. Отрезок называется направленным, если для него указано начало и конец.
Например, если мы говорим , что [А,В] направленный отрезок, то это означает, что А – начало отрезка, а В – его конец, и в дальнейшем будем его обозначать чертой сверху:  . На рисунке направленный отрезок отмечается стрелкой, указывающей конец отрезка. Часто приходится рассматривать так называемый вырожденный или нулевой направленный отрезок, то есть отрезок, у которого концы совпадают:
. На рисунке направленный отрезок отмечается стрелкой, указывающей конец отрезка. Часто приходится рассматривать так называемый вырожденный или нулевой направленный отрезок, то есть отрезок, у которого концы совпадают: 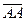 .
.
Под длиной ненулевого направленного отрезка  понимаем число |А,В|, а для нулевого направленного отрезка длина считается равной нулю.
понимаем число |А,В|, а для нулевого направленного отрезка длина считается равной нулю.
Определение 5. Ненулевые отрезки  и
и  называется сонаправленными, если соответствующие лучи [А,В) и [С,D) сонаправленные, соответственно, противоположно направленными, если соответствующие лучи [А,В) и [С,D) противоположно направленные.
называется сонаправленными, если соответствующие лучи [А,В) и [С,D) сонаправленные, соответственно, противоположно направленными, если соответствующие лучи [А,В) и [С,D) противоположно направленные.
Обозначаем аналогично: 
 ,
,  ¯
¯  .
.
Для нулевого направленного отрезка можно говорить, что он сонаправлен с любым направленным отрезком, но сам направления не определяет.
Определение 6. Отрезки  и
и  называются эквиполлентными, если они имеют одинаковое направление и их длины равны.
называются эквиполлентными, если они имеют одинаковое направление и их длины равны.
Будем обозначать эквиполлентные направленные отрезки:  ~
~  .
.
Теорема 2. Отношение эквиполлентности направленных отрезков является отношением эквивалентности.
Доказательство. Рефлексивность  ~
~  , симметричность, если
, симметричность, если  ~
~  , то
, то  ~
~  и транзитивность, если
и транзитивность, если  ~
~  , а
, а  ~
~ 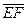 , то
, то  ~
~ 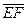 очевидны, так как длина отрезка и направление (теорема 1) соответствующих лучей обладают этими свойствами.
очевидны, так как длина отрезка и направление (теорема 1) соответствующих лучей обладают этими свойствами.
Теорема 3. Направленные отрезки  и
и  эквиполлентны тогда и только тогда, когда середины отрезков [AD] и [BC] совпадают.
эквиполлентны тогда и только тогда, когда середины отрезков [AD] и [BC] совпадают.
Доказательство. Пусть направленные отрезки  и
и  эквиполлентны и не лежат на одной прямой. Тогда мы имеем параллелограмм АВDC. Отрезки [AD] и [BC] являются диагоналями этого параллелограмма. Следовательно, середины отрезков [AD] и [BC] совпадают.
эквиполлентны и не лежат на одной прямой. Тогда мы имеем параллелограмм АВDC. Отрезки [AD] и [BC] являются диагоналями этого параллелограмма. Следовательно, середины отрезков [AD] и [BC] совпадают.
Пусть середины отрезков [AD] и [BC] совпадают. Тогда АВDC – параллелограмм, так как его диагонали пересекаются и делятся этой точкой пополам. Отсюда получим, что направленные отрезки  и
и  лежат на параллельных прямых, имеют одинаковую длину и лежат по одну сторону от прямой (АС), то есть направленные отрезки
лежат на параллельных прямых, имеют одинаковую длину и лежат по одну сторону от прямой (АС), то есть направленные отрезки  и
и  эквиполлентны.
эквиполлентны.
Если направленные отрезки  и
и  эквиполлентны и лежат на одной прямой, то, очевидно, середины отрезков [AD] и [BC] совпадают. Верно и обратное. Теорема доказана..
эквиполлентны и лежат на одной прямой, то, очевидно, середины отрезков [AD] и [BC] совпадают. Верно и обратное. Теорема доказана..
Пример 1. Дан параллелограмм АВСD и точка пересечения его диагоналей О. Сколько направленных отрезков задают данные точки А, В, С, D, О. Указать среди них ненулевые сонаправленные и противоположно направленные отрезки. Решение.
О
Для решения задачи достаточно перечислить все направленные отрезки, рассматривая рисунок. Итак,  ,
, 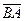 ,
, 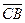 ,
, 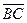 ,
,  ,
, 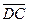 ,
, 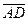 ,
, 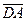 ,
, 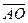 ,
, 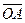 ,
, 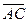 ,
, 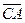 ,
, 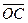 ,
, 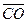 ,
, 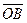 ,
, 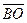 ,
, 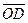 ,
, 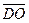 ,
, 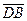 ,
, 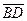 ,
, 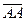 ,
, 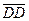 ,
, 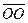 ,
, 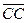 ,
, 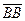 . Всего мы имеем 25 направленных отрезков. Из них выбираем сонаправленные направленные отрезки :
. Всего мы имеем 25 направленных отрезков. Из них выбираем сонаправленные направленные отрезки :  ↑↑
↑↑ 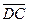 ,
, 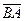 ↑↑
↑↑  ,
, 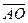 ↑↑
↑↑ 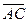 ↑↑
↑↑ 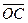 ,
, 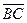 ↑↑
↑↑ 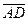 ,
, 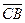 ↑↑
↑↑ 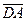 ,
, 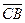 ↑↑
↑↑ 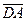 ,
, 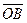 ↑↑
↑↑ 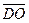 ↑↑
↑↑ 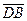 ,
, 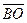 ↑↑
↑↑ 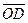 ↑↑
↑↑ 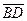 .
.
Противоположно направленные отрезки:  ↑↓
↑↓ 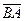 ,
,  ↑↓
↑↓ 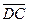 ,
,  ↑↓
↑↓  ,
,
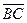 ↑↓
↑↓ 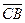 ,
, 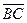 ↑↓
↑↓ 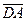 ,
, 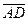 ↑↓
↑↓ 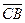 ,
, 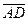 ↑↓
↑↓ 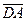 ,
, 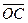 ↑↓
↑↓ 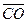 ,
, 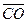 ↑↓
↑↓ 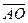 ,
, 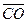 ↑↓
↑↓ 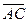 ,
, 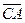 ↑↓
↑↓ 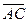 ,
, 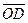 ↑↓
↑↓ 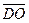 ,
, 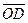 ↑↓
↑↓ 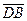 ,
, 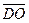 ↑↓
↑↓ 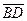 ,
, 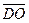 ↑↓
↑↓ 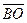 и т. д.
и т. д.
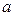 и
и 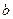 обозначаем:
обозначаем: 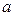 ||
|| 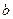 .
.








 . На рисунке направленный отрезок отмечается стрелкой, указывающей конец отрезка. Часто приходится рассматривать так называемый вырожденный или нулевой направленный отрезок, то есть отрезок, у которого концы совпадают:
. На рисунке направленный отрезок отмечается стрелкой, указывающей конец отрезка. Часто приходится рассматривать так называемый вырожденный или нулевой направленный отрезок, то есть отрезок, у которого концы совпадают: 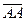 .
. понимаем число |А,В|, а для нулевого направленного отрезка длина считается равной нулю.
понимаем число |А,В|, а для нулевого направленного отрезка длина считается равной нулю. и
и  называется сонаправленными, если соответствующие лучи [А,В) и [С,D) сонаправленные, соответственно, противоположно направленными, если соответствующие лучи [А,В) и [С,D) противоположно направленные.
называется сонаправленными, если соответствующие лучи [А,В) и [С,D) сонаправленные, соответственно, противоположно направленными, если соответствующие лучи [А,В) и [С,D) противоположно направленные.
 ,
,  ¯
¯  .
. и
и  называются эквиполлентными, если они имеют одинаковое направление и их длины равны.
называются эквиполлентными, если они имеют одинаковое направление и их длины равны. ~
~  .
. ~
~  , симметричность, если
, симметричность, если  ~
~  , то
, то  ~
~  и транзитивность, если
и транзитивность, если  ~
~  , а
, а  ~
~ 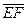 , то
, то  ~
~ 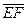 очевидны, так как длина отрезка и направление (теорема 1) соответствующих лучей обладают этими свойствами.
очевидны, так как длина отрезка и направление (теорема 1) соответствующих лучей обладают этими свойствами. и
и  эквиполлентны тогда и только тогда, когда середины отрезков [AD] и [BC] совпадают.
эквиполлентны тогда и только тогда, когда середины отрезков [AD] и [BC] совпадают. и
и  эквиполлентны и не лежат на одной прямой. Тогда мы имеем параллелограмм АВDC. Отрезки [AD] и [BC] являются диагоналями этого параллелограмма. Следовательно, середины отрезков [AD] и [BC] совпадают.
эквиполлентны и не лежат на одной прямой. Тогда мы имеем параллелограмм АВDC. Отрезки [AD] и [BC] являются диагоналями этого параллелограмма. Следовательно, середины отрезков [AD] и [BC] совпадают. и
и  лежат на параллельных прямых, имеют одинаковую длину и лежат по одну сторону от прямой (АС), то есть направленные отрезки
лежат на параллельных прямых, имеют одинаковую длину и лежат по одну сторону от прямой (АС), то есть направленные отрезки  и
и  эквиполлентны.
эквиполлентны. и
и  эквиполлентны и лежат на одной прямой, то, очевидно, середины отрезков [AD] и [BC] совпадают. Верно и обратное. Теорема доказана..
эквиполлентны и лежат на одной прямой, то, очевидно, середины отрезков [AD] и [BC] совпадают. Верно и обратное. Теорема доказана..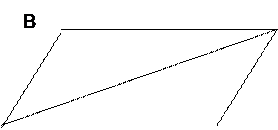

 ,
, 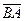 ,
, 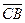 ,
, 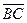 ,
,  ,
, 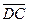 ,
, 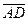 ,
, 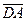 ,
, 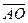 ,
, 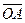 ,
, 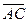 ,
, 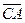 ,
, 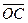 ,
, 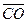 ,
, 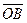 ,
, 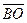 ,
, 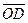 ,
, 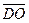 ,
, 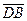 ,
, 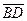 ,
, 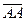 ,
, 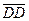 ,
, 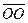 ,
, 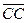 ,
, 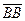 . Всего мы имеем 25 направленных отрезков. Из них выбираем сонаправленные направленные отрезки :
. Всего мы имеем 25 направленных отрезков. Из них выбираем сонаправленные направленные отрезки :  ↑↑
↑↑ 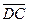 ,
, 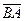 ↑↑
↑↑  ,
, 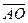 ↑↑
↑↑ 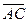 ↑↑
↑↑ 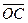 ,
, 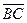 ↑↑
↑↑ 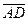 ,
, 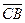 ↑↑
↑↑ 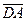 ,
, 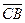 ↑↑
↑↑ 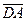 ,
, 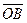 ↑↑
↑↑ 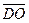 ↑↑
↑↑ 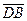 ,
, 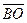 ↑↑
↑↑ 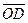 ↑↑
↑↑ 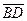 .
. ↑↓
↑↓ 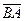 ,
,  ↑↓
↑↓ 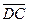 ,
,  ↑↓
↑↓  ,
,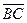 ↑↓
↑↓ 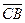 ,
, 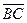 ↑↓
↑↓ 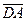 ,
, 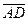 ↑↓
↑↓ 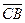 ,
, 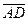 ↑↓
↑↓ 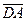 ,
, 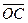 ↑↓
↑↓ 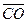 ,
, 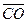 ↑↓
↑↓ 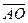 ,
, 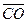 ↑↓
↑↓ 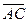 ,
, 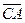 ↑↓
↑↓ 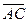 ,
, 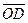 ↑↓
↑↓ 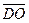 ,
, 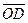 ↑↓
↑↓ 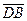 ,
, 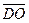 ↑↓
↑↓ 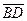 ,
, 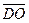 ↑↓
↑↓ 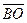 и т. д.
и т. д.