Метод симметричных составляющих

Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими.Различают симметричные составляющие прямой, обратнойи нулевойпоследовательностей, которые различаются порядком чередования фаз.

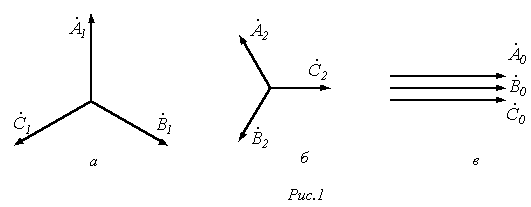
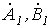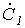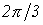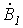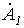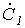Симметричную систему прямой последовательности образуют (см. рис. 1,а) три одинаковых по модулю вектора и со сдвигом друг по отношению к другу на рад., причем отстает от , а - от .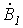

Введя, оператор поворота 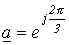, для симметричной системы прямой последовательности можно записать

.

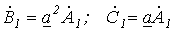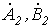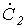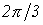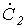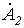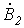Симметричная система обратной последовательности образована равными по модулю векторами и с относительным сдвигом по фазе на рад., причем теперь отстает от , а - от 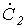(см. рис. 1,б). Для этой системы имеем

.

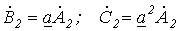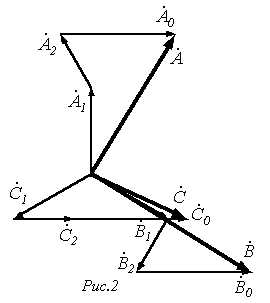Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в):

.

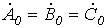При сложении трех указанных систем векторов получается несимметричная система векторов (см. рис. 2).

Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно,

;

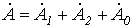(1)

;

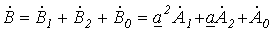(2)

.

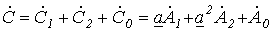(3)

Таким образом, получена система из трех уравнений относительно трех неизвестных 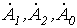, которые, следовательно, определяются однозначно. Для нахождения 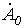сложим уравнения (1)…(3). Тогда, учитывая, что 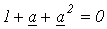, получим

.

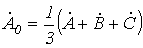(4)

Для нахождения 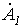умножим (2) на 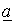, а (3) – на 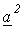, после чего полученные выражения сложим с (1). В результате приходим к соотношению

.

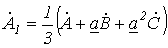(5)

Для определения 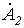с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на 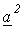и 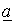. В результате имеем:

.

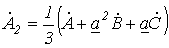(6)

Формулы (1)…(6) справедливы для любой системы векторов 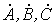, в том числе и для симметричной. В последнем случае .

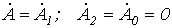В заключение раздела отметим, что помимо вычисления симметричные составляющие могут быть измерены с помощью специальных фильтров симметричных составляющих, используемых в устройствах релейной защиты и автоматики.

Свойства симметричных составляющих токов
и напряжений различных последовательностей

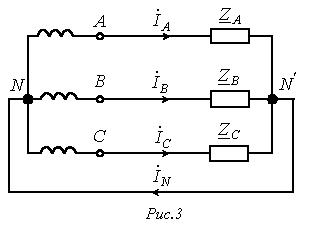Рассмотрим четырехпроводную систему на рис. 3. Для тока в нейтральном проводе имеем

.

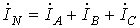Тогда с учетом (4)

,

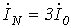(7)

т.е. ток в нейтральном проводе равен утроенному току нулевой последовательности.

Если нейтрального провода нет, то 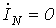и соответственно нет составляющих тока нулевой последовательности.

Поскольку сумма линейных напряжений равна нулю, то в соответствии с (4) линейные напряжения не содержат составляющих нулевой последовательности.

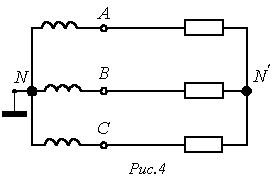Рассмотрим трехпроводную несимметричную систему на рис. 4.

Здесь

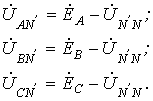
Тогда, просуммировав эти соотношения, для симметричных составляющих нулевой последовательности фазных напряжений можно записать

.

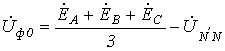Если система ЭДС генератора симметрична, то из последнего получаем

.

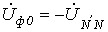(8)

Из (8) вытекает:

· в фазных напряжениях симметричного приемника отсутствуют симметричные составляющие нулевой последовательности;

· симметричные составляющие нулевой последовательности фазных напряжений несимметричного приемника определяются величиной напряжения смещения нейтрали;

· фазные напряжения несимметричных приемников, соединенных звездой, при питании от одного источника различаются только за счет симметричных составляющих нулевой последовательности; симметричные составляющие прямой и обратной последовательностей у них одинаковы, поскольку однозначно связаны с соответствующими симметричными составляющими линейных напряжений.

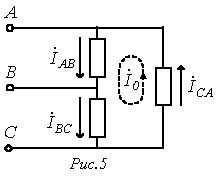При соединении нагрузки в треугольник фазные ток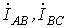и и 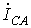могут содержать симметричные составляющие нулевой последовательности 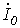. При этом 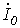(см. рис. 5) циркулирует по контуру, образованному фазами нагрузки.

Сопротивления симметричной трехфазной цепи
для токов различных последовательностей

Если к симметричной цепи приложена симметричная система фазных напряжений прямой (обратной или нулевой) последовательностей, то в ней возникает симметричная система токов прямой (обратной или нулевой) последовательности. При использовании метода симметричных составляющих на практике симметричные составляющие напряжений связаны с симметричными составляющими токов той же последовательности. Отношение симметричных составляющих фазных напряжений прямой (обратной или нулевой) последовательности к соответствующим симметричным составляющим токов называется комплексным сопротивлением прямой

,

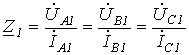Обратной

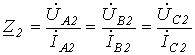
и нулевой

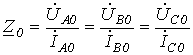
Последовательностей.

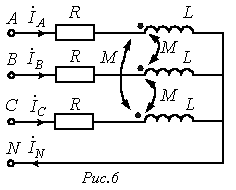
Пусть имеем участок цепи на рис. 6. Для фазы А этого участка можно записать

.

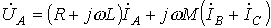(9)

Тогда для симметричных составляющих прямой и обратной последовательностей с учетом, того, что 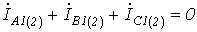, на основании (9) имеем

.

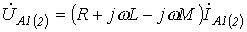Отсюда комплексные сопротивления прямой и обратной последовательностей одинаковы и равны:

.

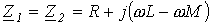Для симметричных составляющих нулевой последовательности с учетом равенства 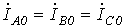соотношение (9) трансформируется в уравнение

,

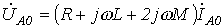откуда комплексное сопротивление нулевой последовательности

.

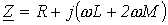В рассмотренном примере получено равенство сопротивлений прямой и обратной последовательностей. В общем случае эти сопротивления могут отличаться друг от друга. Наиболее типичный пример – различие сопротивлений вращающейся машины для токов прямой и обратной последовательностей за счет многократной разницы в скольжении ротора относительно вращающегося магнитного поля для этих последовательностей.

Применение метода симметричных составляющих
для симметричных цепей

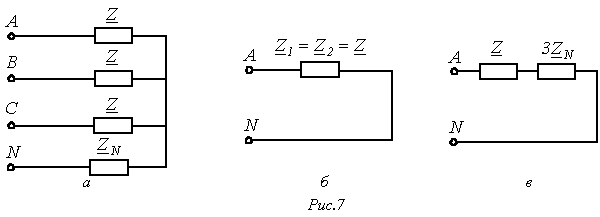
Расчет цепей методом симметричных составляющих основывается на принципе наложения, в виду чего метод применим только к линейным цепям. Согласно данному методу расчет осуществляется в отдельности для составляющих напряжений и токов различных последовательностей, причем в силу симметрии режимов работы цепи для них он проводится для одной фазы (фазы А). После этого в соответствии с (1)…(3) определяются реальные искомые величины. При расчете следует помнить, что, поскольку в симметричном режиме ток в нейтральном проводе равен нулю, сопротивление нейтрального провода никак ни влияет на симметричные составляющие токов прямой и обратной последовательностей. Наоборот, в схему замещения для нулевой последовательности на основании (7) вводится утроенное значение сопротивления в нейтральном проводе. С учетом вышесказанного исходной схеме на рис. 7,а соответствуют расчетные однофазные цепи для прямой и обратной последовательностей (рис. 7,б) и нулевой последовательности (рис. 7,в).

Существенно сложнее обстоит дело при несимметрии сопротивлений по фазам. Пусть в цепи на рис. 3 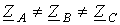. Разложив токи на симметричные составляющие, для данной цепи можно записать

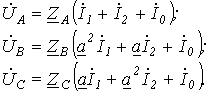(10)

В свою очередь

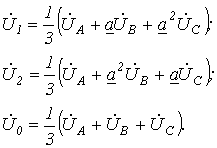(11)

Подставив в (11) значения соответствующих параметров из (10) после группировки членов получим

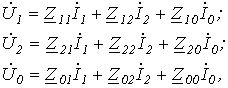(12)

где ;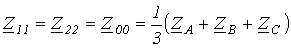

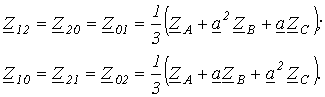
Из полученных соотношений видно, что если к несимметричной цепи приложена несимметричная система напряжений, то каждая из симметричных составляющих токов зависит от симметричных составляющих напряжений всех последовательностей. Поэтому, если бы трехфазная цепь на всех участках была несимметрична, рассматриваемый метод расчета не давал бы преимуществ. На практике система в основном является симметричной, а несимметрия обычно носит локальный характер. Это обстоятельство, как будет показано в следующей лекции, значительно упрощает анализ.

На всех участках цепи, где сопротивления по фазам одинаковы, 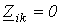для i¹k. Тогда из (12) получаем

.

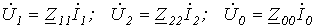Лекция N 20

Теорема об активном двухполюснике
для симметричных составляющих

В тех случаях, когда трехфазная цепь в целом симметрична, а несимметрия носит локальный характер (местное короткое замыкание или обрыв фазы, подключение несимметричной нагрузки), для расчета удобно применять теорему об активном двухполюснике.

При мысленном устранении несимметрии (несимметричного участка) для оставшейся цепи имеет место симметричный режим холостого хода. В соответствии с методом эквивалентного генератора теперь необходимо определить эквивалентные ЭДС и входные сопротивления симметричной цепи. В общем случае – при несимметрии в системе фазных напряжений источника – помимо эквивалентной ЭДС прямой последовательности 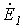будут также иметь место эквивалентные ЭДС обратной 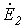и нулевой 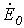последовательностей. Однако обычно напряжения генераторов симметричны – тогда 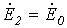. Величина 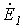, соответствующая напряжению холостого хода 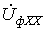на зажимах подключения локальной несимметрии, определяется при отключении локальной несимметричной нагрузки любым известным методом расчета линейных цепей, причем в силу симметрии цепи расчет проводится для одной фазы.

В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая предварительно преобразуется известными методами в пассивную цепь. При этом при расчете входного сопротивления нулевой последовательности 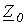необходимо учитывать только те участки цепи, которые соединены с нейтральным проводом или заземленной нейтральной точкой, т.е. принимать во внимание только те ветви, по которым могут протекать токи нулевой последовательности. Схемы для расчета входных сопротивлений прямой и обратной последовательностей одинаковы, однако в случае вращающихся машин величины этих сопротивлений различны.

Поскольку в отдельности для каждой симметричной последовательности имеет место симметричный режим, расчет указанным методом ведется на одну фазу с использованием расчетных схем для прямой (рис. 1,а), обратной (рис. 1,б) и нулевой (рис. 1,в) последовательностей.

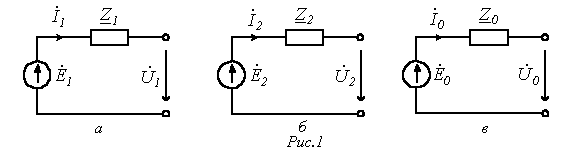
Данным схемам соответствуют соотношения

;

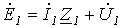(1)

;

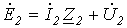(2)

.

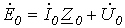(3)

Поскольку соотношений три, а число входящих в них неизвестных шесть 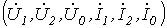, необходимо составление трех дополнительных уравнений, учитывающих конкретный вид несимметрии.

Рассмотрим некоторые типовые примеры применения метода.

Однополюсное короткое замыкание на землю (рис. 2).

.

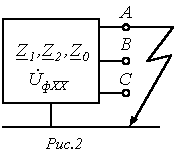
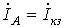Поскольку фаза А замкнута на землю, то дополнительные уравнения имеют вид

;

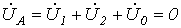(4)

;

.

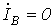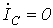Тогда

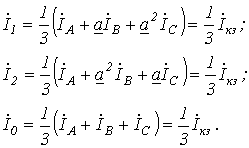
С учетом последних соотношений уравнения (1)…(3) можно записать в виде

;

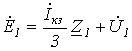(5)

;

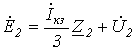(6)

.

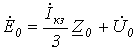(7)

Принимая во внимание (4), а также то, что источник питания симметричный 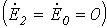, просуммируем (5), (6) и (7):

,

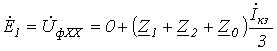откуда получаем

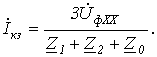
Двухполюсное короткое замыкание без земли (рис. 3).

Для рассматриваемого случая можно записать

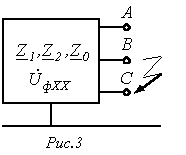
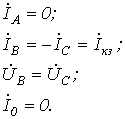
Последнее равенство объясняется отсутствием пути для протекания токов нулевой последовательности.

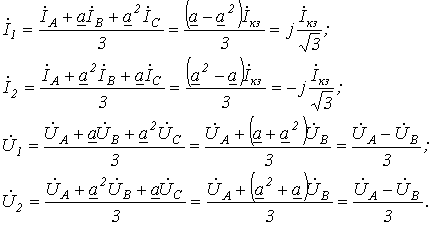
Из двух последних соотношений вытекает, что 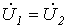. При этом 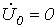, так как 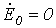и .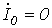

Подставив полученные выражения для напряжений и токов прямой и обратной последовательностей в (1) и (2), запишем

;

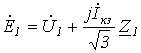(8)

.

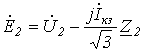(9)

Вычитая из (8) соотношение (9) и учитывая, что в силу симметрии источника 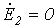, получим

,

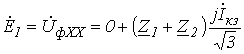откуда

.

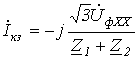Обрыв линейного провода (рис. 4) – определить напряжение в месте разрыва.

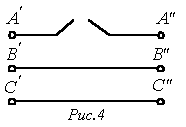В рассматриваемом случае дополнительные уравнения имеют вид

;

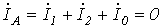(10)

;

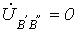(11)

.

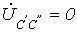(12)

Из соотношений (11) и (12) вытекает равенство:

.

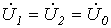(13)

На основании (1)…(3) с учетом (13) запишем

.

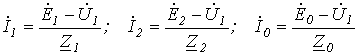Принимая во внимание симметричность источника 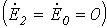, подставим последние выражения в (10):

,

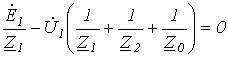- откуда

.

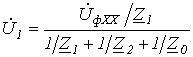Таким образом, искомое напряжение

.

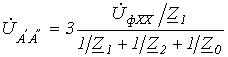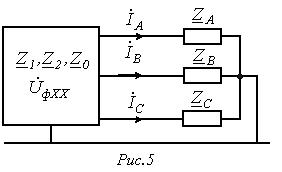
Подключение несимметричной нагрузки 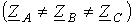к симметричной цепи (рис. 5).

Учитывая, что 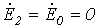, подставим в уравнения (1)…(3) определенные в предыдущей лекции выражения 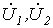и 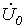(см. соотношение (12) в лекции №19):

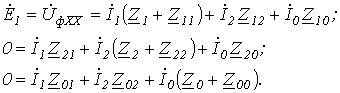
Решая данную систему уравнений, находим 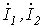и 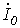. Тогда

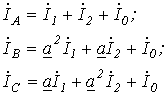
и .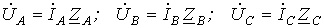

В рассмотренных примерах предполагалось, что необходимые для анализа цепи параметры 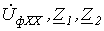и 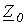предварительно определены. Рассмотрим их расчет на примере предыдущей задачи для некоторой схемы на рис. 6.

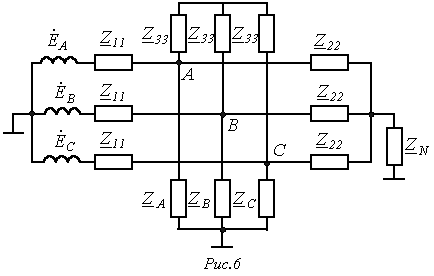
Поскольку при отключении несимметричной нагрузки 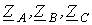оставшаяся часть схемы будет работать в симметричном режиме, для определения 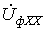получаем расчетную однофазную схему на рис. 7.

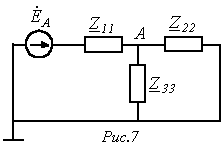Из нее

.

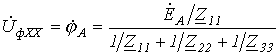Схема для определения входных сопротивлений прямой 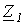и обратной 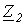последовательностей одна и та же и соответствует цепи на рис. 8,а. В соответствии с ней

.

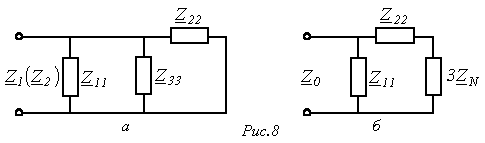
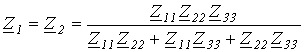Схема для определения 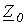, полученная с учетом возможных путей протекания токов нулевой последовательности, приведена на рис. 8,б. Из нее

.
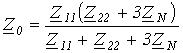