Проводимости цепи переменного тока. Треугольник проводимостей. Коэффициент мощности. Выражения проводимостей через сопротивления цепи.

Синусоидальный ток имеет ряд преимуществ по сравнению с постоянным током, поэтому в электроэнергетике наиболее распространены цепи переменного тока (в энергетике синусоидальный ток обычно называют переменным). Синусоидальный ток экономичнее при производстве, передаче и использовании электроэнергии. С помощью простого устройства (трансформатора) можно осуществить дробление электроэнергии. Устройства синусоидального тока нашли широкое применение в различных отраслях промышленности, в электроприводе, промышленной электронике, электротехнологии, радиоэлектронике, бытовой технике. В промышленности основным источником переменного напряжения является синхронный генератор, который будет рассмотрен далее. В радиоэлектронике синусоидальные колебания получают с помощью электронных схем – автогенераторов.

Рассмотрим основные понятия, характеризующие синусоидальную функцию, например, напряжение u(t):

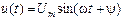, (3.1)

график которой (временная диаграмма) показан на рис. 3.1а.

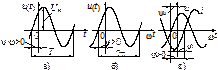
Рис. 3.1. Временные диаграммы синусоидальных функций

Наибольшее значение U_m синусоидальной функции называют амплитудой. Наименьший отрезок времени T, через который значение функции повторяется, называют периодом (рис.3.1а). Частота f=1/T – количество периодов в секунду. Частоту измеряют в герцах (Гц). Частота промышленной сети составляет 50Гц. Аргумент синусоидальной функции α=ωt+ψ называют фазой. Величина ψ равна фазе при t=0, т.е. ψ – начальная фаза. Фазу и начальную фазу измеряют в радианах. Угловой частотой ω называют скорость изменения аргумента функции, т.е. ω=dα/dt. Измеряют угловую частоту в рад/с. Угловая частота ω связана с частотой f соотношением

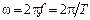. (3.2)

При изображении синусоидальных функций на временных диаграммах удобно по горизонтальной оси откладывать не время t, а величину ωt, измеряемую в радианах (рис. 3.1б). В этом случае начальная фаза ψ определяется смещением синусоиды по горизонтали относительно начала координат. Если синусоида смещена влево, то ψ>0, вправо, то ψ<0. Величину u(t), зависящую от текущего значения времени t, называют мгновенным значением и обозначают строчной (малой) буквой. Аналогично обозначают мгновенное значение тока i(t) и ЭДС e(t).

Из (3.1) следует, что синусоидальная функция имеет три параметра: 1) амплитуду U_m; 2) угловую частоту ω; 3) начальную фазу ψ. В электротехнике широко используется четвертый (производный) параметр синусоидальной функции – действующее значение U. Действующим значением периодической функции называют ее среднеквадратичное значение за период, т.е.

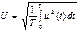. (3.3)

Если в (3.3) подставить (3.1), то получим:

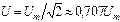, (3.4)

т.е. действующее значение синусоидальной функции меньше ее амплитуды в 2^0,5 раз. Действующее значение напряжения бытовой однофазной сети составляет 220В. Аналогично определяются действующие значения других синусоидальных величин, например тока 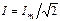, и ЭДС 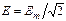. Действующие значения обозначаются прописной (большой) буквой, например U, I, E, Φ, но, в отличие от амплитуды U_m, I_m, E_m, Φ_m, не имеют индекса m.

Сдвигом фаз φ называют разность начальных фаз двух синусоидальных колебаний одинаковой частоты ω. Если сравниваются фазы напряжения u(t) и тока i(t), то для φ условились: φ=ψ_u–ψ_i. На рис. 3.1в ψ_u>0; ψ_i<0; φ>0.