Глава 1. Обыкновенные дифференциальные уравнения
Глава 1. Обыкновенные дифференциальные уравнения
Дифференциальные уравнения первого порядка
П.1.1.1. Основные понятия
Опр. Диф.уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции.
Если независимая переменная одна, то уравнение называется обыкновенным, если же независимых переменных две или более, то уравнение называется диф.уравнением в частных производных.
Обозначение: 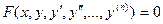 ,
, 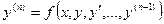 (разрешенное относительно старшей производной),
(разрешенное относительно старшей производной), 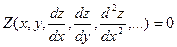 .
.
Опр. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ.
Рассмотрим примеры ДУ:
1. 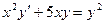 ; ОДУ ____________ порядка
; ОДУ ____________ порядка
2. 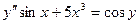 ; ОДУ ___________ порядка
; ОДУ ___________ порядка
3. 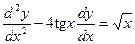 ; ОДУ _________ порядка
; ОДУ _________ порядка
4. 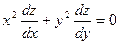 ; Уравнение в частных производных _________ порядка
; Уравнение в частных производных _________ порядка
Данная глава посвящена только ОДУ, т.е. уравнение в частных производных рассматриваться здесь не будут, поэтому говоря ДУ, мы всюду далее будем понимать ОДУ.
В данном параграфе рассматриваются ДУ первого порядка.
Общий вид ДУ первого порядка: 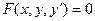 или в разрешенном виде относительно производной
или в разрешенном виде относительно производной 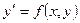 .
.
Опр. Решением ДУ называется такая дифференцируемая функция 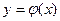 , которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
, которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
Процесс нахождения решения ДУ называется интегрированием ДУ.
Опр. Общим решением ДУ первого порядка 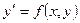 в области D называется функция
в области D называется функция 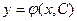 , обладающая свойствами:
, обладающая свойствами:
1) Она является решением данного уравнения при любых значениях постоянной 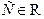 ;
;
2) Для любого начального условия 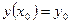 такого, что
такого, что 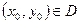 , существует единственное значение
, существует единственное значение 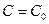 , при котором решение
, при котором решение 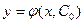 удовлетворяет заданному начальному условию.
удовлетворяет заданному начальному условию.
Опр. Всякое решение 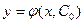 , получающееся из общего решения
, получающееся из общего решения 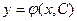 при конкретном значении
при конкретном значении 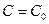 , называется частным решением.
, называется частным решением.
Опр. Задача, в которой требуется найти частное решение уравнения 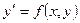 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 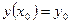 , называется задачей Коши.
, называется задачей Коши.
С геометрической точки зрения общее решение ДУ представляет собой семейство так называемых интегральных кривых на координатной плоскости, зависящее от одной произвольной постоянной С, а график частного решения, удовлетворяющего начальному условию 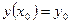 , - есть кривая этого семейства, проходящая через точку
, - есть кривая этого семейства, проходящая через точку 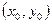 .
.
Теорема о существовании и единственности решения ДУ (теорема Коши).
Если в уравнении 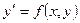 функция
функция 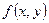 и её частная производная
и её частная производная 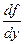 по y непрерывны в некоторой области D на плоскости Оxy, то существует единственное решение
по y непрерывны в некоторой области D на плоскости Оxy, то существует единственное решение 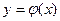 этого уравнения, удовлетворяющее начальному условию
этого уравнения, удовлетворяющее начальному условию 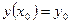 .
.
С геометрической точки зрения: существует и притом единственная функция 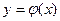 , график которой проходит через точку
, график которой проходит через точку 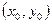 .
.
ДУ второго порядка
П.1.2.1. Основные понятия
Опр. Уравнение, связывающее независимую переменную x, неизвестную функцию y(x), а также её первые две производные 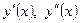 , называется ДУ второго порядка.
, называется ДУ второго порядка.
Вид: 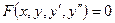 или
или 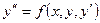 .
.
Задача Коши в случае ДУ второго порядка выглядит:
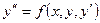 ,
, 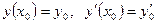 .
.
Опр. Решением ДУ второго порядка называется всякая функция 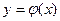 , которая при подстановке вместо
, которая при подстановке вместо 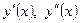 в это уравнение обращает его в тождество.
в это уравнение обращает его в тождество.
Опр. Общим решением ДУ второго порядка называется функция 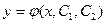 , зависящая от двух произвольных постоянных
, зависящая от двух произвольных постоянных 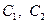 и такая, что:
и такая, что:
1) Она является решением этого уравнения при любых конкретных значениях 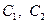 ;
;
2) При любых допустимых начальных условиях 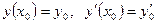 можно подобрать такие значения
можно подобрать такие значения 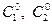 постоянных, что функция
постоянных, что функция 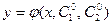 будет удовлетворять этим начальным условиям.
будет удовлетворять этим начальным условиям.
Опр. Любая функция 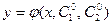 , получающаяся из общего решения при конкретных значениях
, получающаяся из общего решения при конкретных значениях 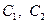 , называется частным решением этого уравнения.
, называется частным решением этого уравнения.
П.1.3.1. Основные понятия
Опр. Уравнение вида 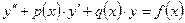 (1), где
(1), где 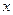 - независимая переменная,
- независимая переменная, 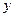 - искомая функция,
- искомая функция, 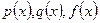 - заданные функции, причем
- заданные функции, причем 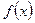 непрерывна на отрезке
непрерывна на отрезке 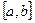 , называется линейным ДУ II порядка.
, называется линейным ДУ II порядка.
Если 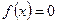 , то уравнение (1) называется однородным, если
, то уравнение (1) называется однородным, если 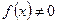 , то уравнение (1) называется неоднородным.
, то уравнение (1) называется неоднородным.
Выразим 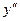 из уравнения (1):
из уравнения (1):
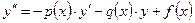 (2)
(2)
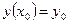 (3)
(3)
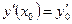 (4)
(4)
Задача (2) – (4) есть задача Коши для линейного ДУ второго порядка.
Глава 1. Обыкновенные дифференциальные уравнения
