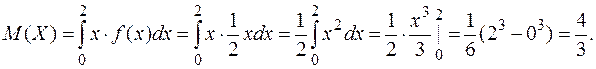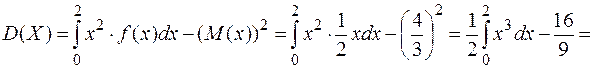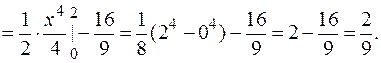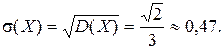Непрерывные случайные величины.
Функция распределения. Плотность распределения.
Числовые характеристики непрерывных случайных величин
Случайная величина называется непрерывной, если она принимает любое значение из некоторого конечного или бесконечного интервала возможных значений.
Функция распределения непрерывной случайной величины определяется так же, как для дискретных случайных величин и является непрерывной. Она имеет те же свойства. Кроме того, для функции распределения непрерывной случайной величины справедливы свойства:
1. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
2. 
.
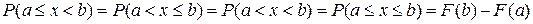Плотностью распределения вероятностей (дифференциальной функцией распределения) непрерывной случайной величины Х называют производную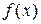 
от функции распределения 
:
.
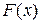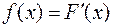Вероятность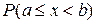 
того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a; b), равна:
.
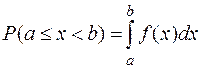Если известна функция плотности распределения 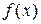, то функция распределения 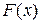находится по формуле:
.
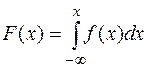Свойства плотности распределения
1. 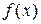является неотрицательной функцией: 
.
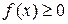2. 
.
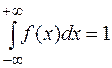Геометрический смысл свойства 2 состоит в том, что площадь криволинейной трапеции, расположенной под графиком плотности распределения, равна единице.
Математическим ожиданием непрерывной случайной величины Х называется величина:
.
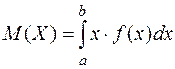Дисперсия непрерывной случайной величины вычисляется по формулам:
,
.
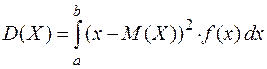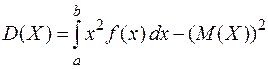Средним квадратическим отклонениемs(Х)непрерывной случайной величины Х называется корень квадратный из дисперсии:
.
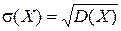Задача. Дана плотность распределения случайной величины Х:
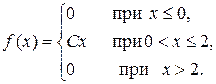
1. Найти параметр С.
2. Построить график плотности распределения .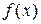
3. Найти вероятность попадания случайной величины Х в промежуток (1; 1,5).
4. Найти функцию распределения случайной величины .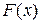
5. Построить график .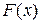
6. Найти числовые характеристики М(Х), D(X),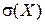
.
Решение.1.Для нахождения неизвестного коэффициента С воспользуемся свойством плотности распределения вероятности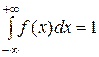 
.
.
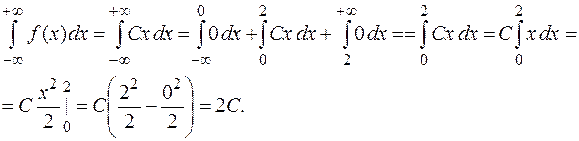
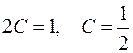С учетом найденного значения константы С, функция плотности распределения имеет вид:
.
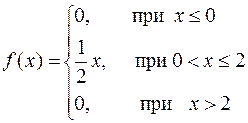2. График функции 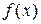имеет вид:
3. Вероятность попадания случайной величины в промежуток (1; 1,5) находится по формуле:
.
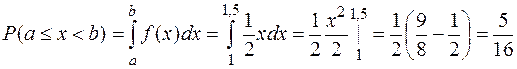4. Найдем интегральную функцию распределения величины Х.
Функция 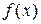задана для разных числовых промежутков разными аналитическими выражениями. С учетом этого найдем :
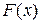при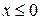 
;
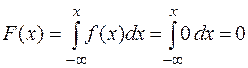при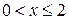 
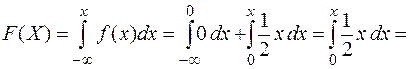
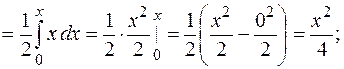
при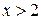 
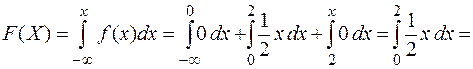
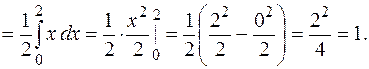
Таким образом, функция распределения имеет вид:
,
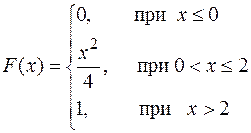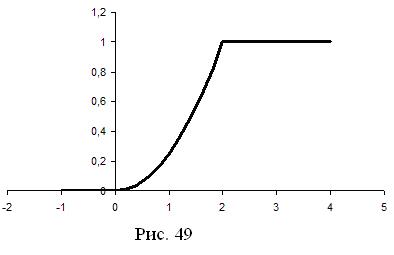
5. График функции распределения имеет вид (рис. 49):
6. Вычислим характеристики случайной величины Х с учетом того, что все ее значения попадают в интервал от 0 до 2.
