Трансформатор с ферромагнитным сердечником
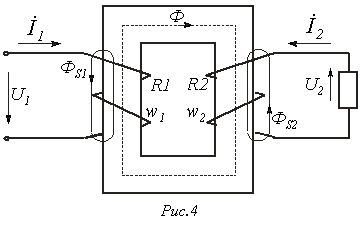 Трансформатор с ферромагнитным сердечником изображен на рис. 4. Здесь
Трансформатор с ферромагнитным сердечником изображен на рис. 4. Здесь 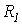 и
и 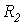 - активные сопротивления первичной и вторичной обмоток с числами витков
- активные сопротивления первичной и вторичной обмоток с числами витков 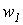 и
и 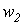 соответственно.
соответственно. 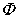 - основной поток, замыкающийся по сердечнику.
- основной поток, замыкающийся по сердечнику. 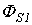 и
и 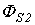 - потоки рассеяния первичной и вторичной обмоток, которым соответствуют индуктивности рассеяния
- потоки рассеяния первичной и вторичной обмоток, которым соответствуют индуктивности рассеяния 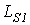 и
и 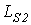 и индуктивные сопротивления рассеяния
и индуктивные сопротивления рассеяния 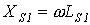 и
и 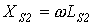 .
.
Основные соотношения, схема замещения и векторная диаграмма для трансформатора с ферромагнитным сердечником приведены в табл. 2.
Таблица 2. Трансформатор с ферромагнитным сердечником
| Вид информации | Уравнения, соотношения, векторная диаграмма | Примечание | |||
| Уравнения для первичной и вторичной цепей Коэффициент трансформации Параметры вторичной цепи, приведенные к первичной: напряжение на нагрузке ток ЭДС сопротивление вторичной обмотки сопротивление нагрузки Уравнения приведенного трансформатора | 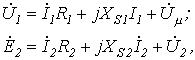 где где 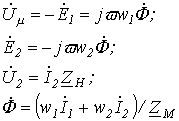 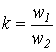 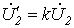 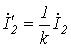 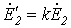 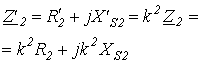 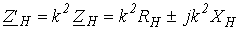 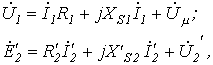 где где 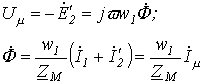 | У правильно сконструирован-ных трансформато-ров при нагрузке, близкой к номинальной, 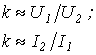 | |||
| Схема замещения | 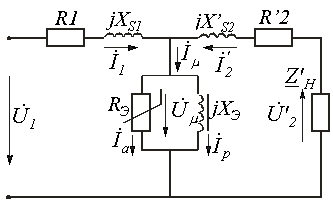 | 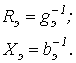 Выражения для Выражения для 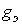 и и 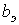 те же, что и для катушки с ферромагнитным сердечником (см. табл. 1) те же, что и для катушки с ферромагнитным сердечником (см. табл. 1) | |||
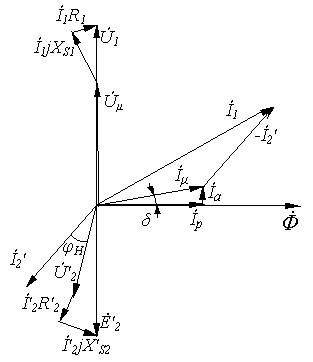
| Векторная диаграмма |
| Диаграмма строится, начиная со вторичного контура, для произвольного расположения 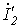 . . 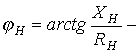 - угол нагрузки - угол нагрузки |
Литература
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретическиеосновы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Из каких составляющих складываются общие потери в стали сердечника ?
- Как на практике подсчитываются потери в стали и намагничивающая мощность ?
- Объясните понятия комплексной магнитной проницаемости и комплексного магнитного сопротивления.
- Нарисуйте последовательную и параллельную схемы замещения катушки с ферромагнитным сердечником и соответствующие им векторные диаграммы.
- Как определяются параметры
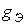 и
и 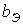 сердечника ?
сердечника ? - Как в схеме замещения нелинейной катушки учитывается воздушный зазор в сердечнике ?
- Нарисуйте схему замещения и векторную диаграмму для трансформатора с ферромагнитным сердечником.
- Катушка со стальным сердечником, имеющим
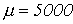 , сечение
, сечение 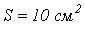 , длину
, длину 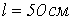 и воздушный зазор
и воздушный зазор 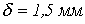 , включена на переменное напряжение
, включена на переменное напряжение 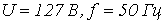 ; число витков обмотки
; число витков обмотки 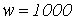 . Пренебрегая рассеянием и потерями в стали сердечника и считая активное сопротивление обмотки равным 100 Ом, определить потребляемый ток и активную мощность.
. Пренебрегая рассеянием и потерями в стали сердечника и считая активное сопротивление обмотки равным 100 Ом, определить потребляемый ток и активную мощность.
Ответ: 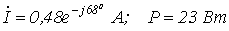 .
.
- При напряжении с действующим значением
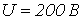 и частотой
и частотой 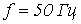 на зажимах дросселя ток в его обмотке
на зажимах дросселя ток в его обмотке 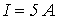 , а потребляемая мощность
, а потребляемая мощность 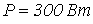 . Число витков обмотки дросселя
. Число витков обмотки дросселя 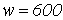 , а ее активное сопротивление
, а ее активное сопротивление 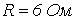 . Измерения показали, что максимальное значение рабочего потока в сердечнике
. Измерения показали, что максимальное значение рабочего потока в сердечнике 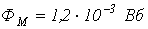 . Определить параметры элементов параллельной схемы замещения дросселя.
. Определить параметры элементов параллельной схемы замещения дросселя.
Ответ: 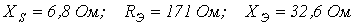 .
.
Особенности расчета переходных процессов в нелинейных цепях Переходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы. Анализ переходных режимов в электрических цепях требует использования динамических характеристик нелинейных элементов, которые, в свою очередь, зависят от происходящих в них динамических процессов и, следовательно, в общем случае наперед неизвестны. Указанное изначально обусловливает в той или иной степени приближенный характер расчета переходных процессов. Переходный процесс в нелинейной цепи может характеризоваться переменной скоростью его протекания в различные интервалы времени. Поэтому понятие постоянной времени в общем случае не применимо для оценки интенсивности протекания динамического режима. Отсутствие общности подхода к интегрированию нелинейных дифференциальных уравнений обусловило наличие в математике большого числа разнообразных методов их решения, нацеленных на различные типы уравнений. Применительно к задачам электротехники все методы расчета по своей сущности могут быть разделены на три группы: – аналитические методы, предполагающие либо аналитическое выражение характеристик нелинейных элементов, либо их кусочно-линейную аппроксимацию; – графические методы, основными операциями в которых являются графические построения, часто сопровождаемые вспомогательными вычислительными этапами; – численные методы, основанные на замене дифференциальных уравнений алгебраическими для приращений переменных за соответствующие интервалы времени. Аналитические методы расчета Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений характеристик нелинейных элементов. Основными аналитическими методами, используемыми при решении широкого круга задач электротехники, являются: – метод условной линеаризации; – метод аналитической аппроксимации; – метод кусочно-линейной аппроксимации. Метод условной линеаризации Метод условной линеаризации применяется в случаях, когда в нелинейном уравнении одно из слагаемых в левой части мало по сравнению с другими, вследствие чего, без внесения существенной погрешности, его можно соответствующим образом линеаризовать. Благодаря этому все уравнение становится линейным для одной из переменных, определяющих характеристику 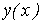 нелинейного элемента, например нелинейного элемента, например 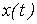 . С использованием этой характеристики находится затем временная зависимость . С использованием этой характеристики находится затем временная зависимость 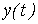 для второй определяющей ее переменной по алгоритму: для второй определяющей ее переменной по алгоритму: 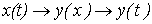 . Метод отличается простотой, однако получаемое с его использованием решение является достаточно приближенным, вследствие чего он в основном применяется для ориентировочных расчетов. В качестве примера использования метода определим максимальное значение тока в цепи на рис. 1, если . Метод отличается простотой, однако получаемое с его использованием решение является достаточно приближенным, вследствие чего он в основном применяется для ориентировочных расчетов. В качестве примера использования метода определим максимальное значение тока в цепи на рис. 1, если 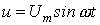 , где , где 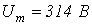 ; ; 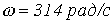 ; ; 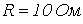 ; ; 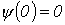 . Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2. . Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2. 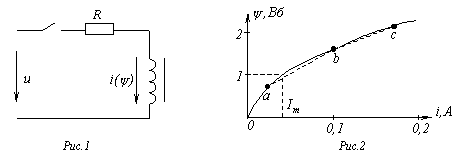 1. Запишем уравнение состояния цепи после коммутации 1. Запишем уравнение состояния цепи после коммутации
2. Используя метод условной линеаризации, определим второе слагаемое в левой части (1) как
где 3. Подставив (2) в (1), получим линейное дифференциальное уравнение
решением которого на основании классического метода расчета переходных процессов является
4. Принужденная составляющая
где Для определения Следует отметить, что в общем случае значения Определив
Поскольку по условию Таким образом,
6. Не решая трансцендентное уравнение, будем считать, что максимальное значение потокосцепления имеет место примерно через полпериода своего изменения, т.е. при
По кривой Примечания: 1. Обычно при использовании метода условной линеаризации для расчета переходного процесса при подключении нелинейной катушки индуктивности к источнику синусоидального напряжения эквивалентная линейная индуктивность 2. Если сопротивление резистора в ветви с нелинейной катушкой достаточно велико, так что
и соответственно кривая Наши рекомендации
|

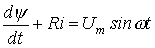 .
. 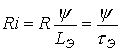 ,
, 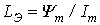 ;
; 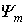 и
и 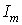 - амплитуды потокосцепления и тока в установившемся послекоммутационном режиме;
- амплитуды потокосцепления и тока в установившемся послекоммутационном режиме; 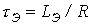 .
.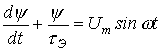 ,
,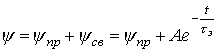 .
.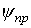 определяется соотношением
определяется соотношением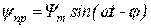 ,
,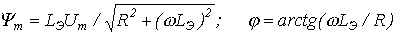 .
.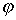 предположим (с последующей проверкой), что
предположим (с последующей проверкой), что 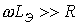 . При этом условии
. При этом условии 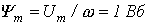 и
и 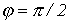 . По зависимости
. По зависимости 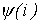 для полученного значения
для полученного значения 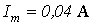 .Тогда
.Тогда 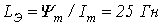 и
и 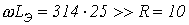 , т.е. сделанное выше предположение корректно.
, т.е. сделанное выше предположение корректно.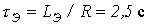 , запишем
, запишем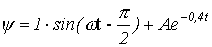 .
.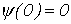 , то
, то 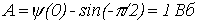 .
.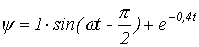 .
. 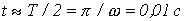 . Подставив это время в (3), получим:
. Подставив это время в (3), получим: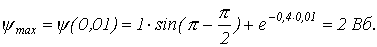
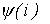 для
для 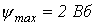 найдем максимальное значение тока
найдем максимальное значение тока 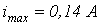 , которое в
, которое в 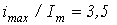 раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним, что для линейной цепи
раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним, что для линейной цепи 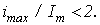
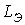 определяется исходя из амплитудных значений тока и потокосцепления в установившемся послекоммутационном режиме, как это и было сделано в рассмотренном выше примере. Однако если необходимо оценить максимально возможное значение тока, то величину индуктивности следует определять по начальному участку вебер–амперной характеристики, где
определяется исходя из амплитудных значений тока и потокосцепления в установившемся послекоммутационном режиме, как это и было сделано в рассмотренном выше примере. Однако если необходимо оценить максимально возможное значение тока, то величину индуктивности следует определять по начальному участку вебер–амперной характеристики, где 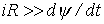 , то следует пренебречь нелинейностью слагаемого
, то следует пренебречь нелинейностью слагаемого 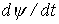 , положив
, положив 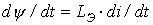 . В этом случае нелинейное уравнение (1) сводится к линейному вида
. В этом случае нелинейное уравнение (1) сводится к линейному вида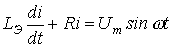 ,
,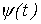 определяется по кривым
определяется по кривым 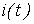 и
и