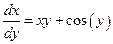Понятие об изогональных траекториях.

Задача. Пусть на плоскости XOY задано однопараметрическое семейство кривых

(I) - 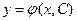. Найти уравнение семейства кривых (II) пересекающих кривые первого семейства под заданным постоянным углом 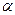. Семейство (II) называют изогональным семейству (I).

Решение.

Выведем д.у. первого семейства также как это делалось выше. Мы получим:

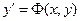
Пользуясь определением изогональности найдем связь между угловыми коэффициентами касательных и кривых семейств I и II в точках их пересечения. Пусть 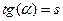, и пусть X и Y координаты точек кривых семейства II. По формуле угла между 2-мя прямыми на плоскости получим:

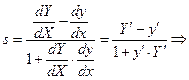
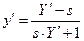
Подставляя последние выражение 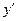в д.у. семейства кривых I получим д.у. искомого семейства II :

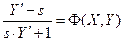
Интегральные кривые этого д.у. и будут искомыми изогональными кривыми.

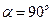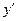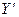Если то траектории называют ортогональными. В этом случае зависимость между и будет наиболее простой: 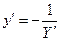, и , т.о. д.у. семейства ортогональных кривых запишется в виде: .

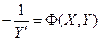Пример. Найти ортогональные траектории к семейству парабол 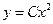. Исключая С из системы 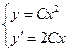получим 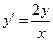тогда д.у. семейства ортогональных траекторий

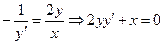интегрируя почленно.

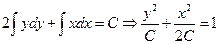-семейство подобных эллипсов.

Сказанное выше относится и к уравнениям вида:

(*)

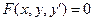
но с небольшими дополнениями. Во-первых, (*) может иметь несколько решений, относительно :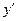

(**)

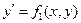
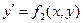и т.д.

Теорема Коши в отношении каждого уравнения обуславливает единственность и существование интегральной кривой, проходящей через 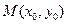. Поэтому, для (*) при выполнении дополнительного условия

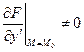
через любую 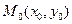, в которой выполнены условия теоремы Коши для (*), проходит столько кривых, сколько решений имеет (*). Для (*) общее решение также зависит от одной константы:

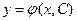
Иногда, решение д.у. приводит к выражениям вида:

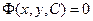
не разрешенных относительно y. Такое соотношение называют общим интегралом д.у.

Пример.

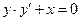будет удовлетворено, если 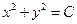- общий интеграл.

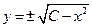- общее решение. Семейство изоклин для (*), найдем из соотношения 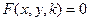, где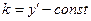

Особые точки и особые решения д.у..

Теорема Коши гарантирует существование решения д.у. 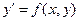, проходящего через 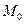, если :

a) 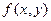непрерывна и б) 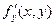- существует и ограничена.

Нарушение хотя бы одного условия может привести к тому, что решение может не существовать, либо оно может быть неединственным. Если теорема Коши нарушается только в отдельных изолированных точках, то они называются особыми точками д.у.. Поведение интегральных кривых в окрестности особых точек может быть различным ( непредсказуемым ).

Если же нарушение условий теоремы Коши имеет место вдоль некоторой кривой, то она может оказаться интегральной кривой данного д.у.. Такую интегральную кривую называют особой, а соответствующее решение – особым решением.

Опр. Решение д.у. первого порядка называется особым, если через любую точку его интегральной кривой проходит по крайней мере еще одна интегральная кривая того же д.у., имеющая в этой точке ту же касательную.

Особое решение, как правило, в общем решении не содержится, т.е. не может быть получено ни при каком выборе константы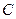

Пример. 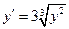- общее решение 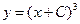, проверяется подстановкой. Условия теоремы Коши нарушены на y=0 т.к.

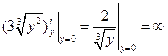
Легко видеть, что y=0 – интегральная кривая, причем особая, т.к. через каждую ее точку 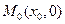проходит входящая в общее решение 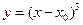, касательной к которой служит y=0. Прямую же y=0 ни при каком С не получим.

7.5. Интегрирование простейших типов д.у. 1-го порядка.

7.5.1. Д.у. с разделяющимися переменными.

Д.у. с разделяющимися переменными называют такое, что разрешив его относительно 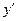получим для нее:

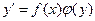
Т.к. 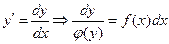- переменные разделены

Т.е. дифференциалы некоторых функци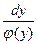й и 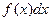и сами функции могут отличаться лишь на постоянную величину, то есть

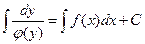- общий интеграл.

Иногда д.у. с разделяющимися переменными может быть в виде:

(A) 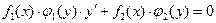или

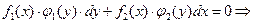
Пример.

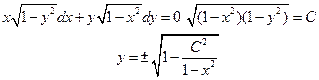
Однако переход от общего интеграла к общему решению не всегда возможен.

Замечание. При делении на 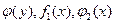возможна “потеря” решений (как в алгебре).

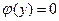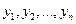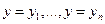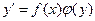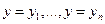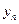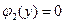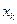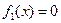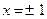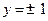Если имеет действительные решения , то прямые - интегральные кривые д.у. . Последние решения могут входить или не входить в общее решение. Чаще всего они являются особыми. Для уравнений вида (A) интегральными будут прямые , где - корни , и , где корни . В разобранном примере прямые и являются интегральными и получаются из общего решения при С=0.

7.5.2. Однородные д.у. 1-го порядка.

Д.у. называется однородным, если , разрешив его относительно 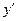, получим функцию, зависящую только от отношения .

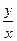(B) 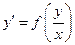, которое, заменой переменной 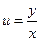преобразуется в уравнение с разделяющимися переменными:

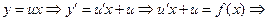
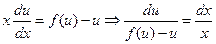- найдя его общее решение и положив в нем 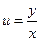, перейдем к общему решению (B).

Пример. ,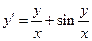

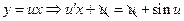
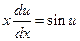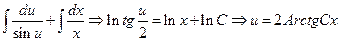или или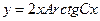

Однородные уравнения часто задаются в виде:

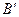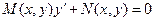( ) или

( )

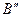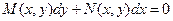
! Признак однородност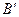и ( ) и ( 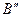) : M и N должны быть однородными функциями одного порядка т.е. :

(*)

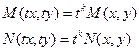
где t – произвольный множитель, k – целое.

Положим в (*)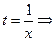

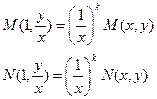
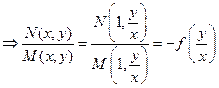
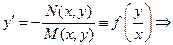
При решении ( ), ( ) 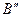нет необходимости перехода к (В) :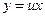

Пример.

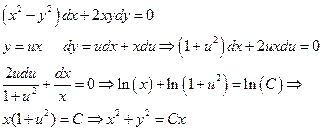
Замечание.

Интегральные кривые однородного уравнения (любого) – семейство подобных кривых с центром подобия в начале координат. Чтобы убедиться в этом достаточно заметить, что изоклины (B) образуют пучок прямых, проходящих через О. Пусть

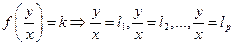(**) - есть корни (**). А это ничто иное как уравнения прямых 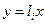. Далее, строя приближенные ломанные, убедимся в правильности замечания.

Дополнительно к уравнениям с разделяющимися переменными:

Уравнения вида 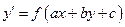с помощью подстановки 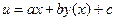сводятся к уравнениям с разделяющимися переменными.

7.5.3. Линейные уравнения 1-го порядка.

Д.у. 1-го порядка называются линейными, есл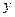и и 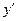входят в это уравнение только в 1-й степени, не перемножаясь друг на друга. Общий вид: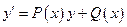

Для интегрирования применим так называемый метод вариации произвольной постоянной. Проинтегрируем линейное однородное уравнение:

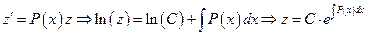
Решение же неоднородного линейного д.у. будим искать в виде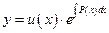

т.е. заменим С на u(x), которую необходимо найти. Т.о. константа заменяется переменной функцией, т.е. варьируется. Найдем 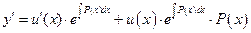и подставим в неоднородное уравнение: после приведения подобных получим:

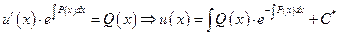
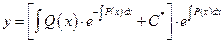- общее решение неоднородного линейного д.у. 1-го порядка.

Пример.

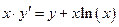найти 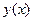проходящую через точку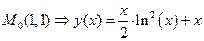

!!! Рассмотреть метод подстановки -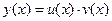

7.5.4. Уравнение Бернулли.

Уравнение вида 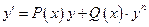, n – любое действительное число. При n=0 – линейное неоднородное, n=1 – линейное однородное. Уравнение Бернулли заменой 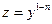, где 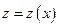новая неизвестная функция, преобразуется в линейное относительно z.

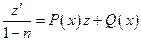
т.к. всякое линейное д.у. может быть проинтегрировано в квадратурах, то это справедливо и по отношению к д.у. Бернулли.

Практически, для интегрирования д.у. Бернулли нет необходимости предварительно преобразовывать его в линейное. Можно применить метод вариации произвольной постоянной, как и для линейного неоднородного.

Пример.

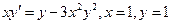, найдем сначала решение д.у. .

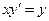Его решение 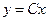. Пусть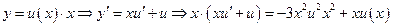

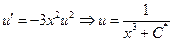Где 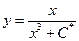- общее решение

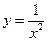- решение задачи Коши,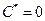

К рассмотренным выше типам д.у. сводятся многие другие с помощью преобразования переменных или перехода к обратной функции.

Пример.

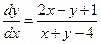заменой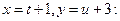

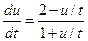
В общем случае:

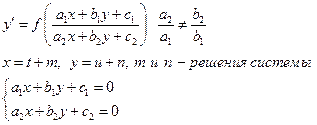
Пример.

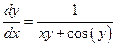сводится к линейному при переходе к обратной функции: