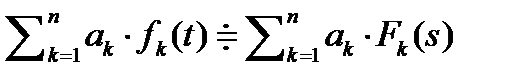Трехфазные цепи: ЭДС, напряжения и токи в системе при соединении фаз генератора и нагрузки звездой, треугольником. Преимущества трехфазной системы.

Трехфазные цепи: ЭДС, напряжения и токи в системе при соединении фаз генератора и нагрузки звездой, треугольником. Преимущества трехфазной системы.

Трехфазная система ЭДС. Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120 градусов.

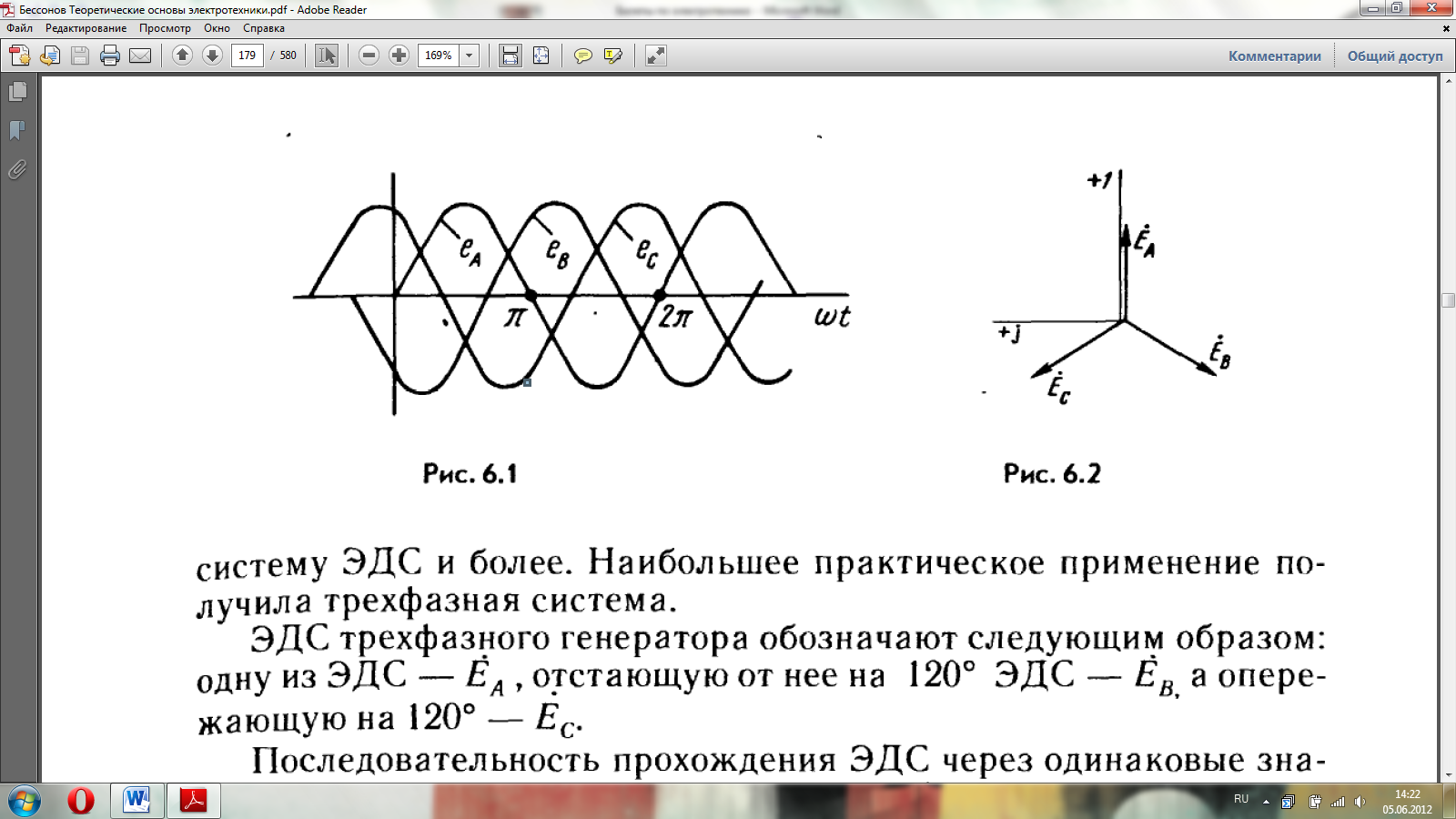
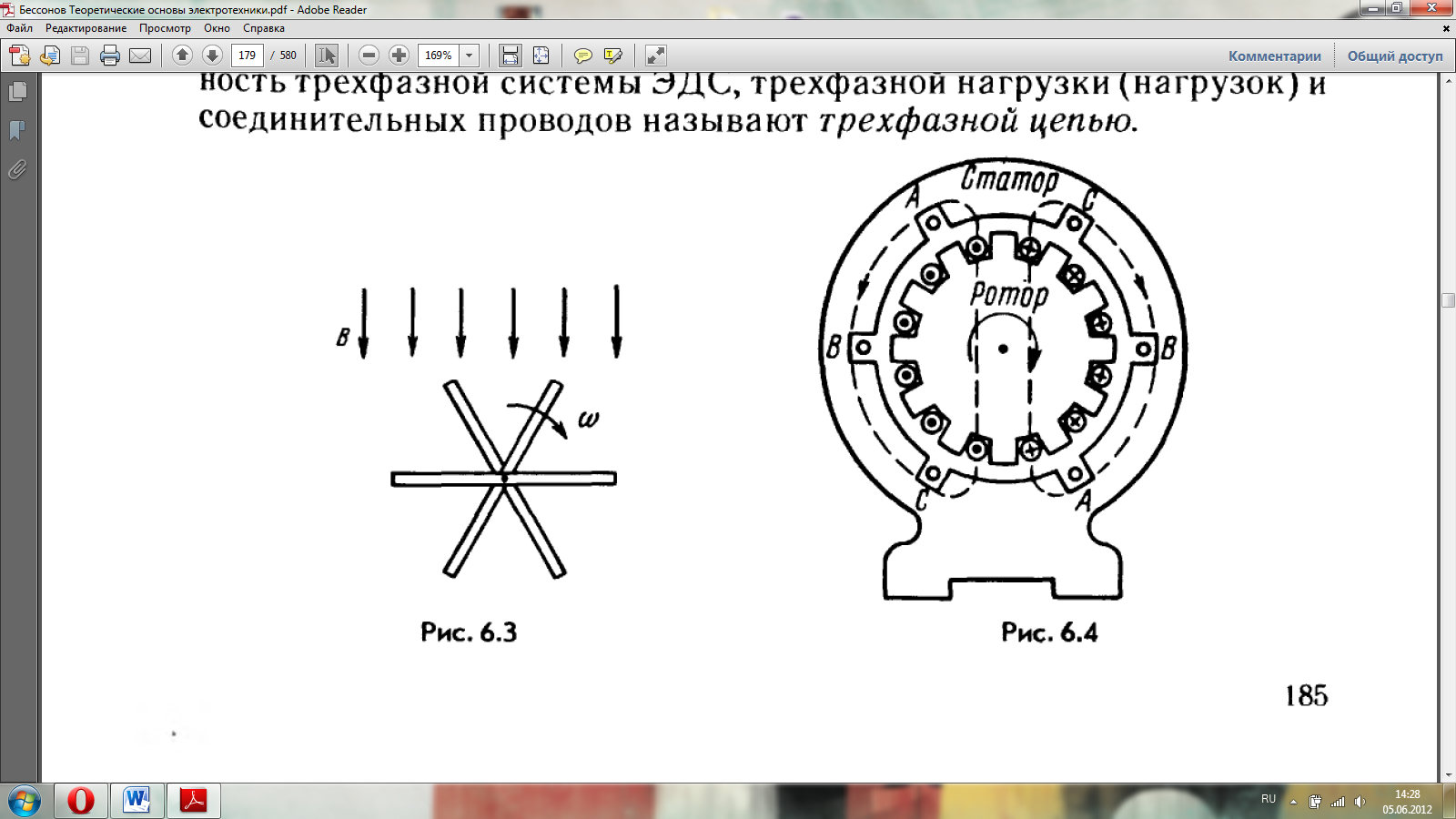
Принцип получения трехфазной системы ЭДС. В равномерном магнитном поле с постоянной угловой скоростью ω вращаются три одинаковых жестко скрепленных друг с другом катушки. Плоскости катушек смещены в пространстве друг относительно друга на 120°. В каждой катушке наводится синусоидальная ЭДС одинаковой амплитуды. По фазе ЭДС катушек сдвинуты на 120°.

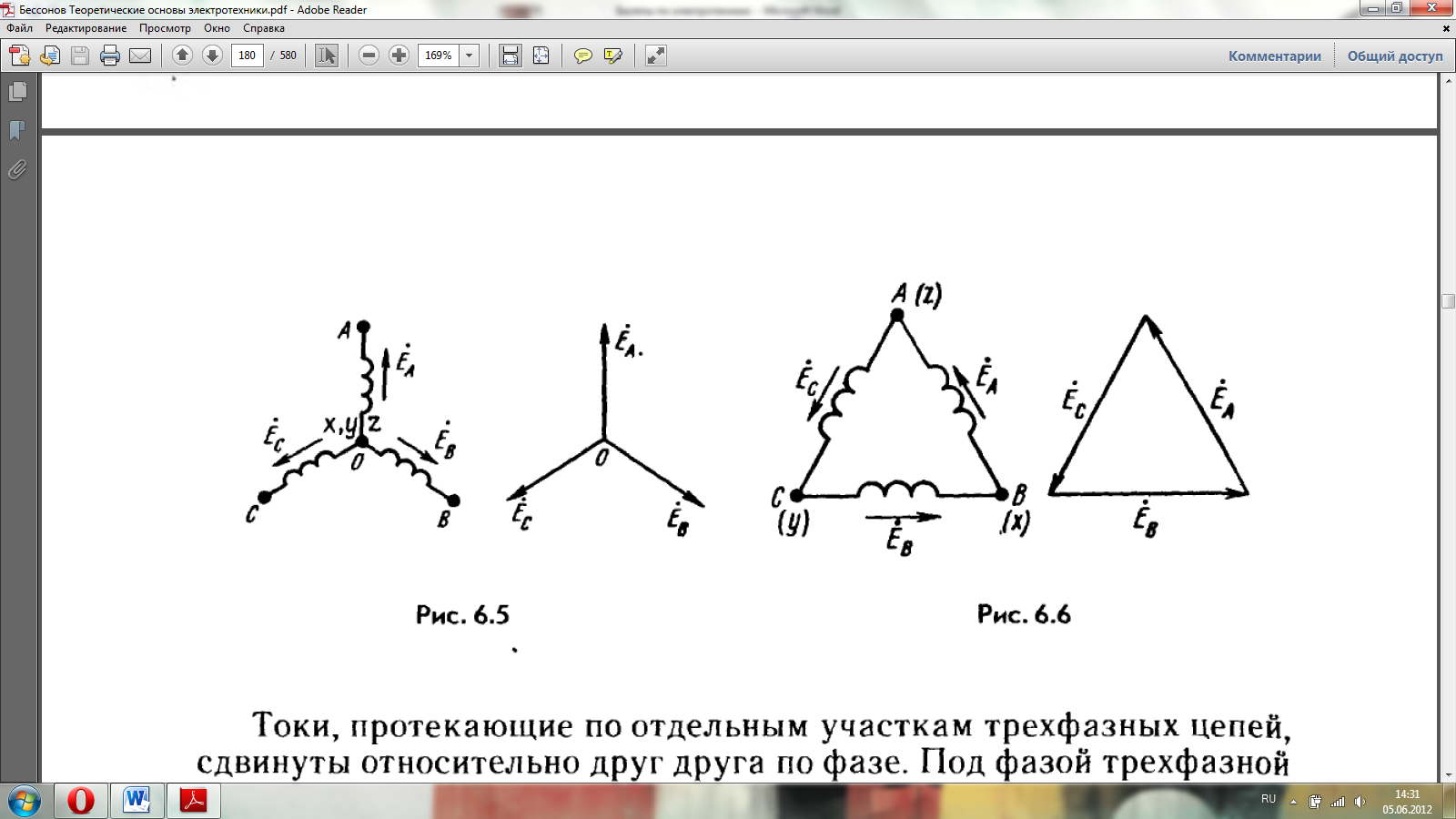
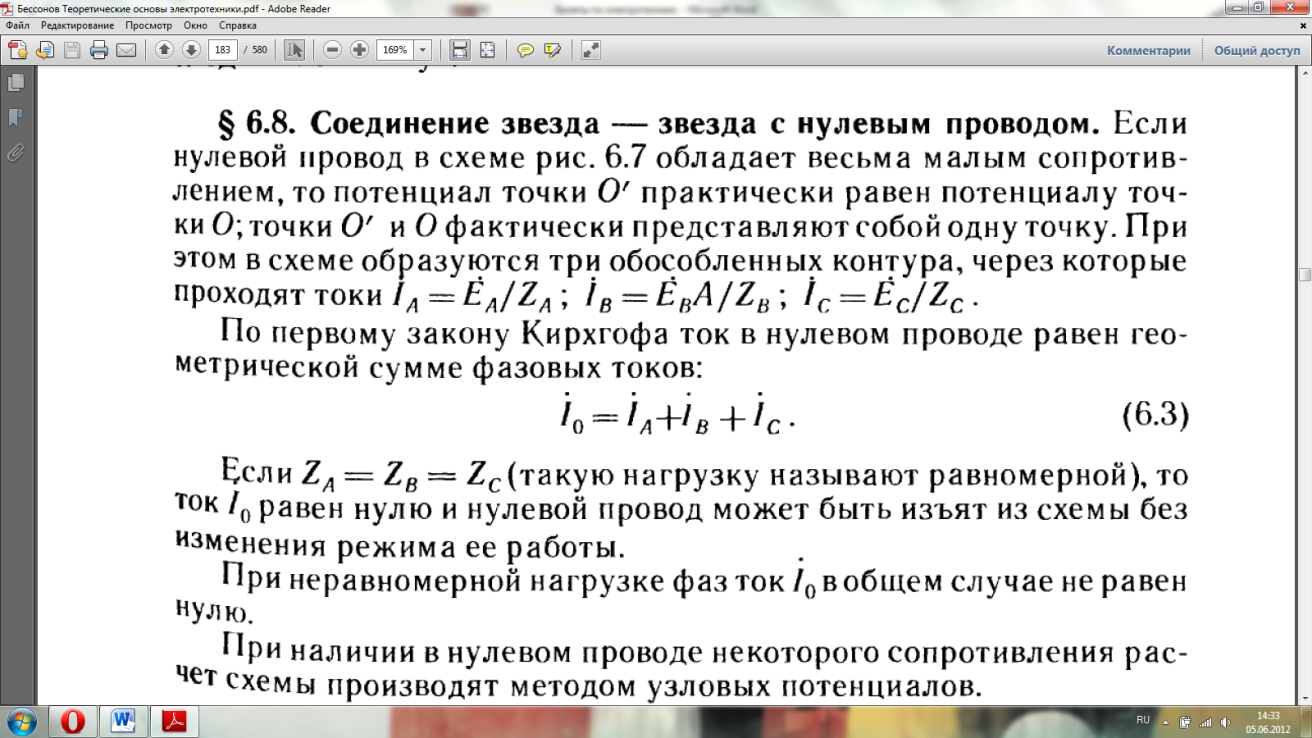
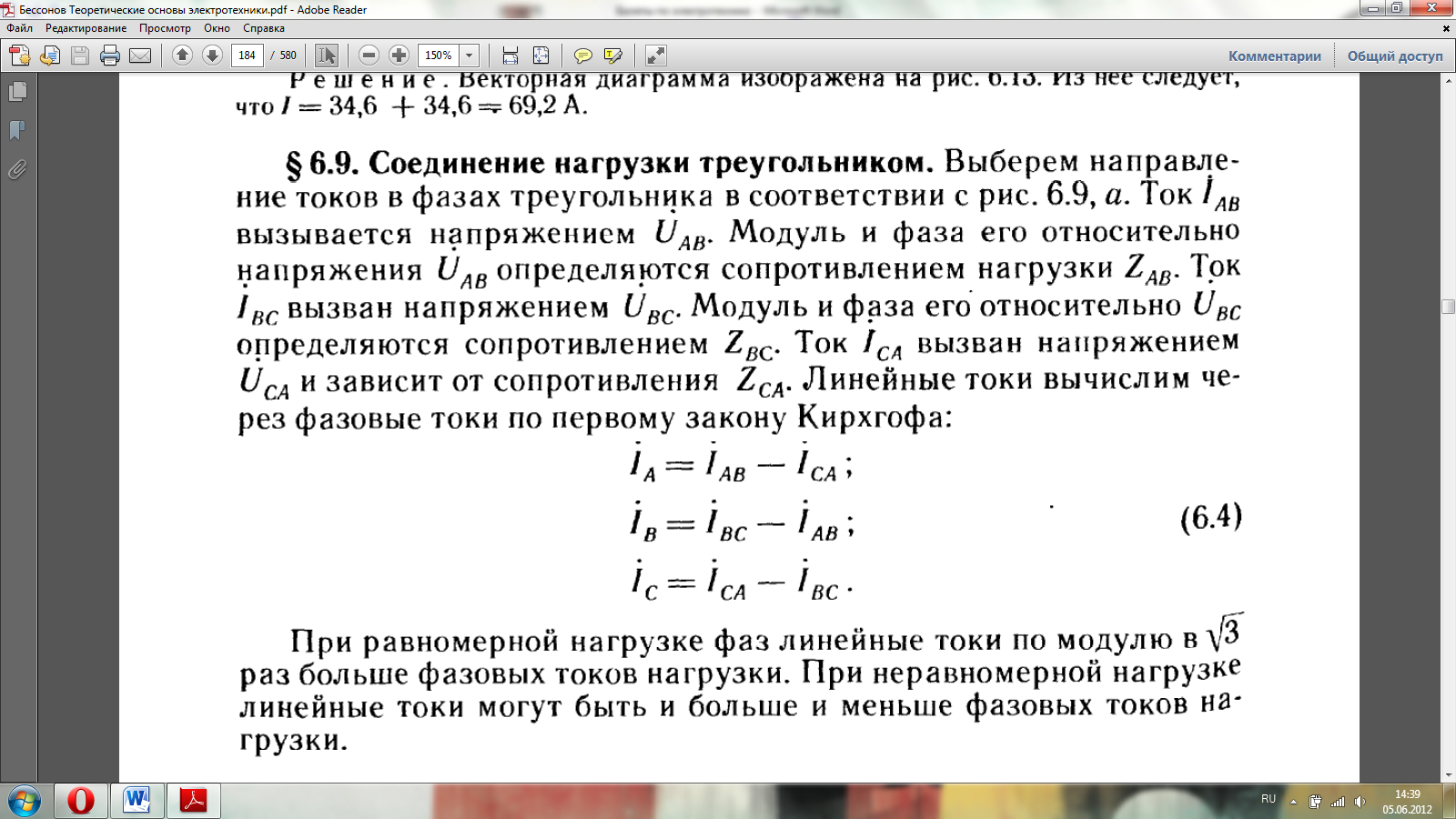
Преимущества трехфазной системы. Широкое распространение трехфазных систем объясняется главным образом тремя основными причинами: 1) передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз; 2) элементы системы – трехфазный синхронный генератор, трехфазный асинхронный двигатель и трехфазный трансформатор – просты в производстве, экономичны и надежны в работе; 3) система обладает свойствами неизменности значения мгновенной мощности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.

2. Операторный метод расчета переходных процессов: преобразование Лапласа; основные свойства преобразования Лапласа; операторное изображение некоторых типовых воздействий.

Переходный процесс – процесс перехода цепи от одного энергетического состояния к другому. Эти процессы вызываются коммутацией эл. цепи. Коммутация – любое изменение параметров цепи, ее конфигурации, а также отключение и подключение источников. Коммутацию считают мгновенной, однако перех. процесс протекает опред. время.

Преобразование Лапласа.

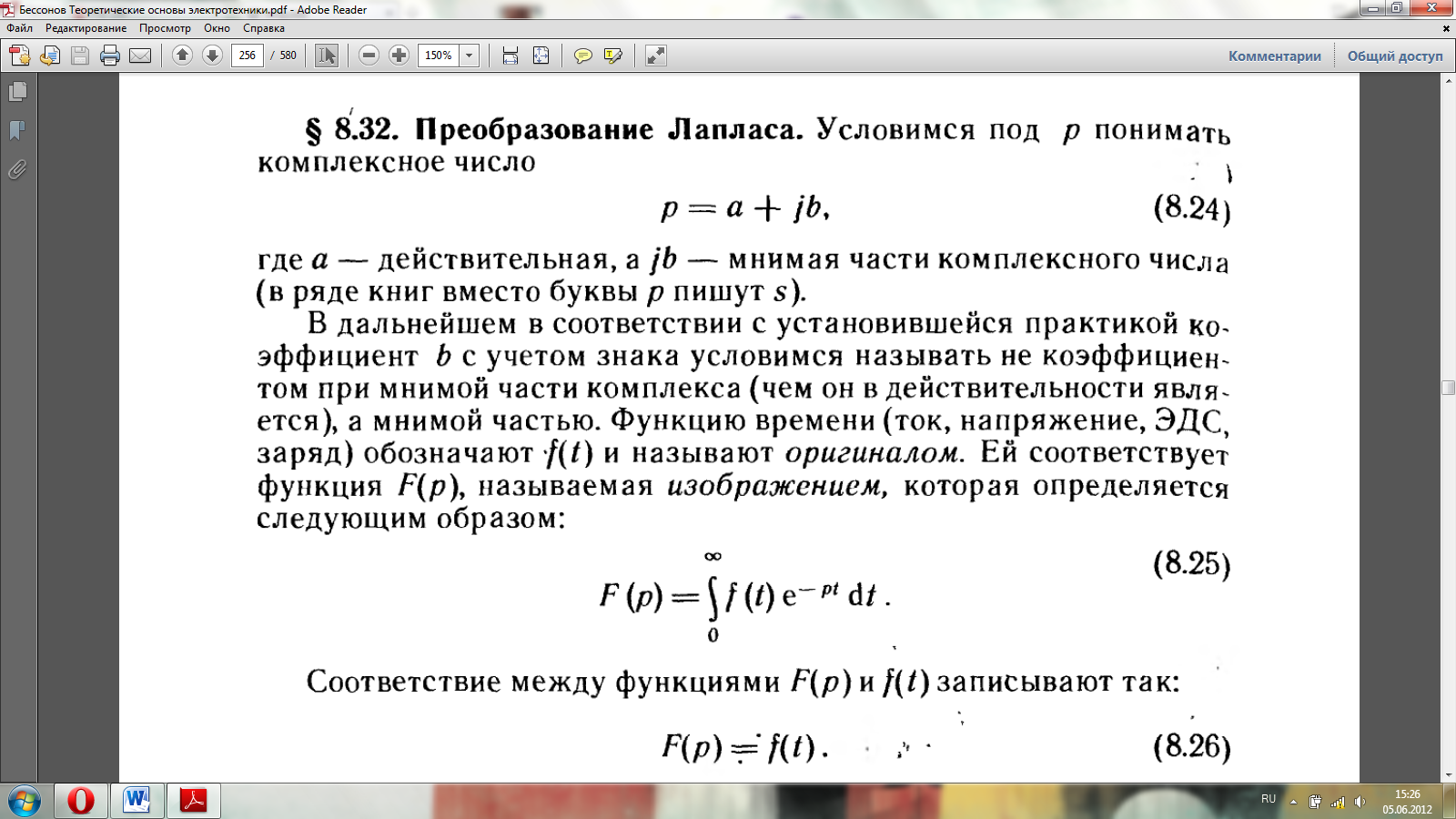
Основные свойства преобразования Лапласа.

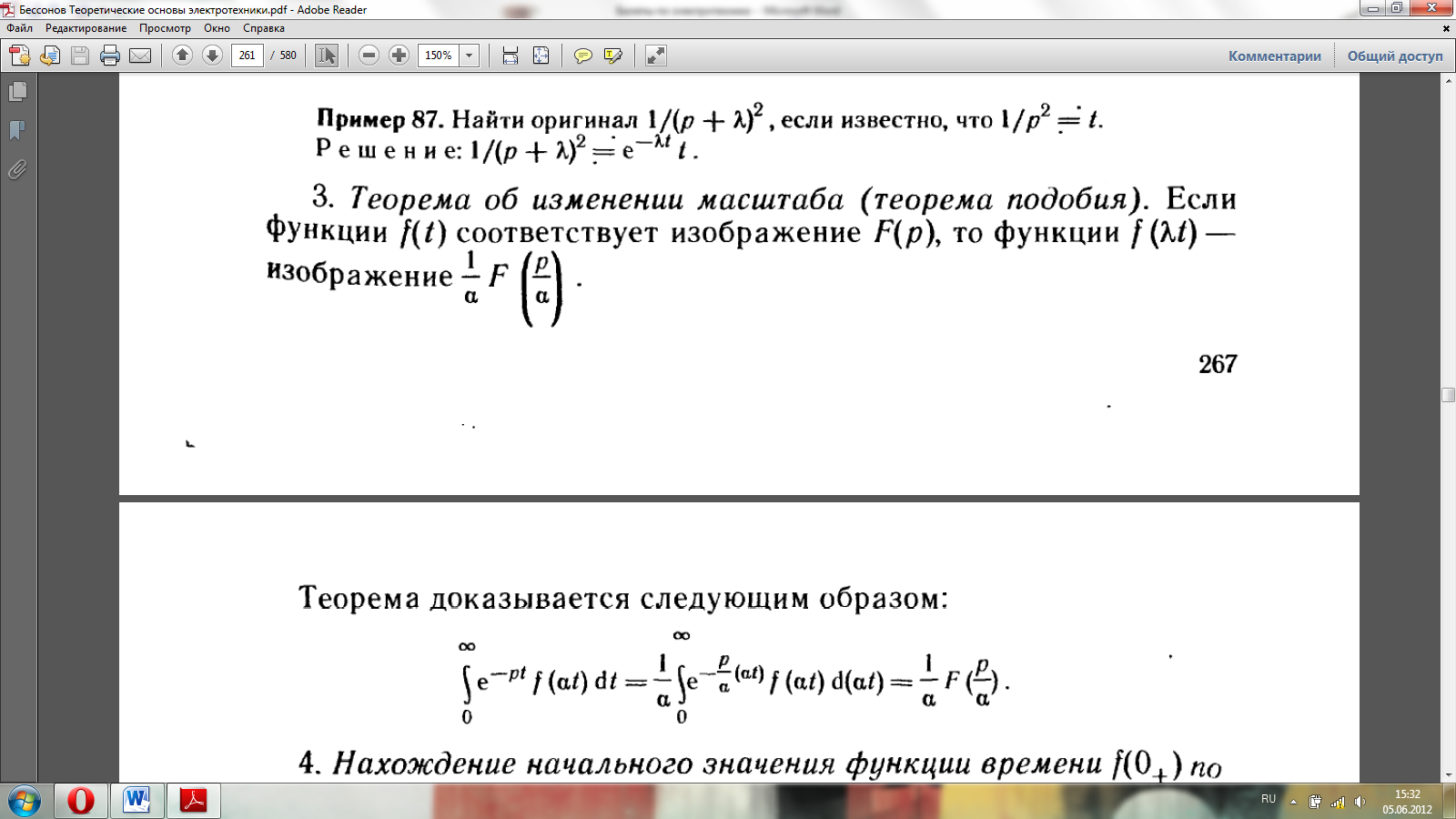
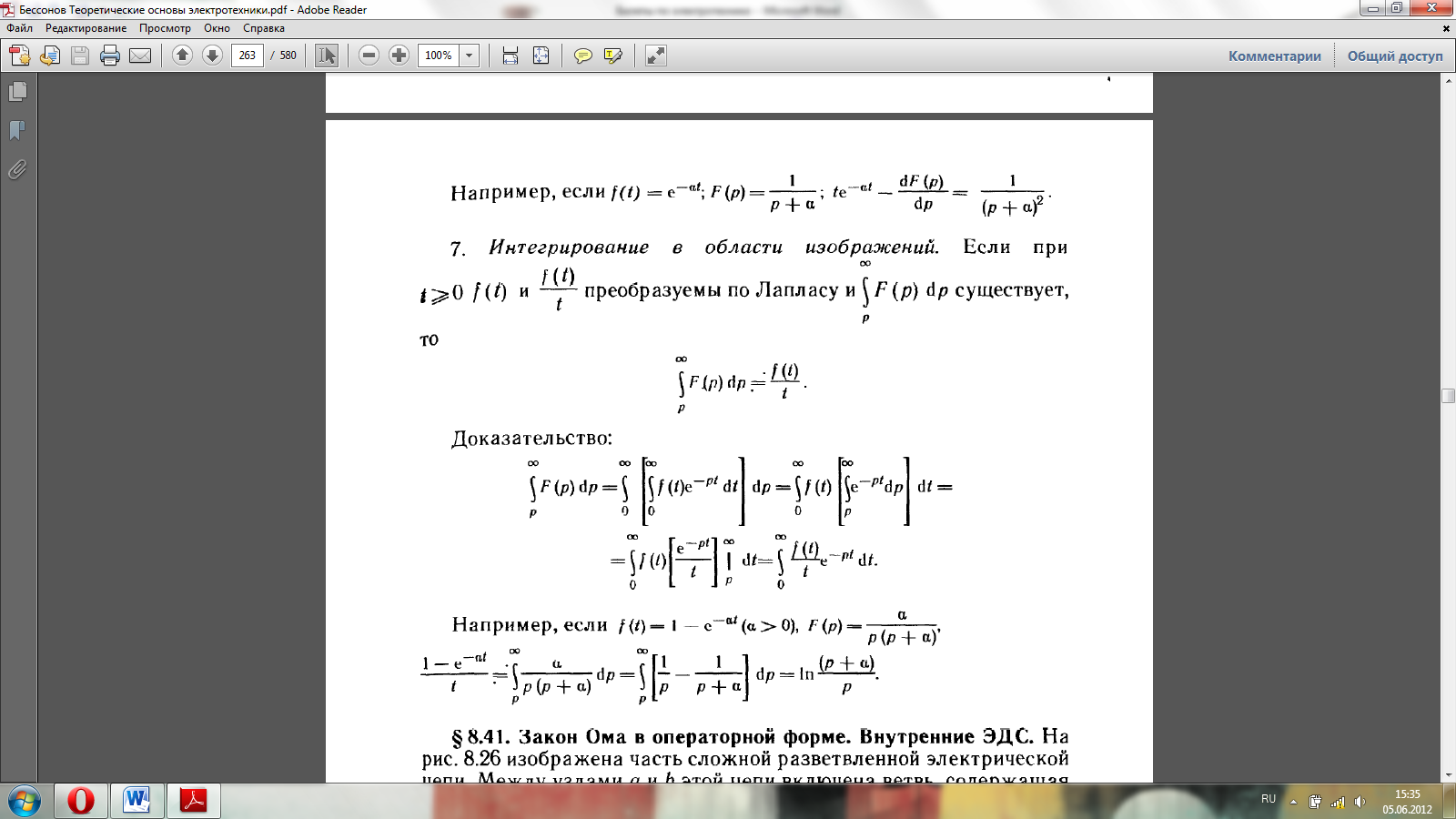
Теор. линейности: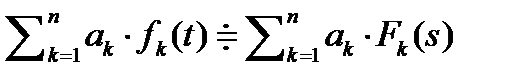

Законы Ома и Кирхгофа в операторной форме, операторные схемы замещения элементов электрической цепи. Закон Ома в операторной форме для R-L-C цепи для ненулевых начальных условий.

Закон Кирхгофа в операторной форме. Первый закон Кирхгофа.

Второй закон Кирхгофа.

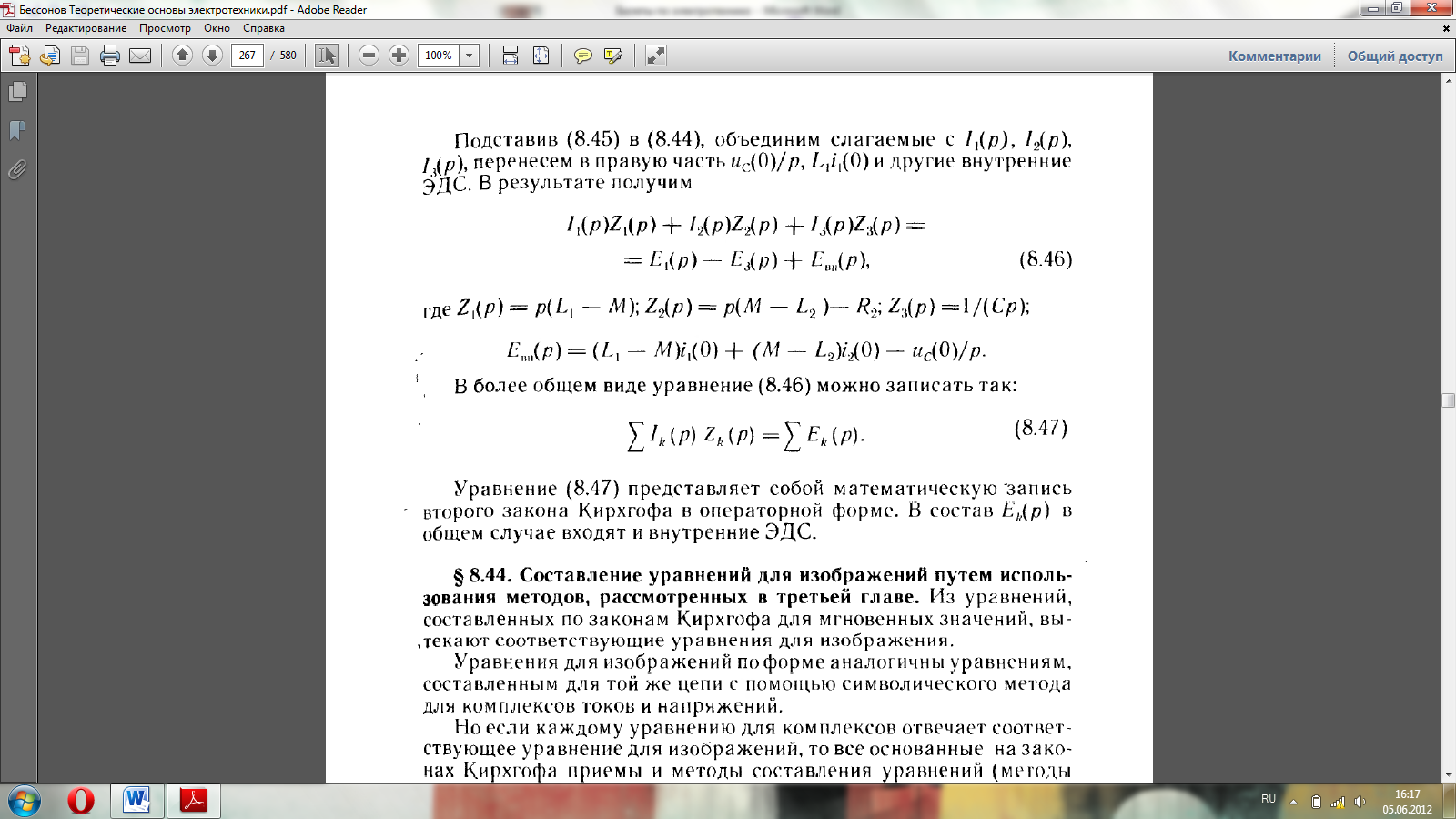
Закон Ома.

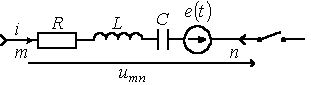
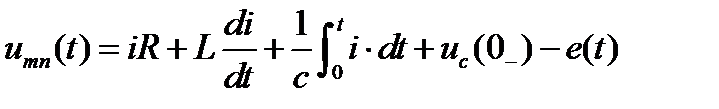
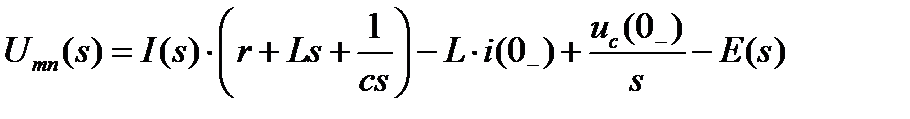
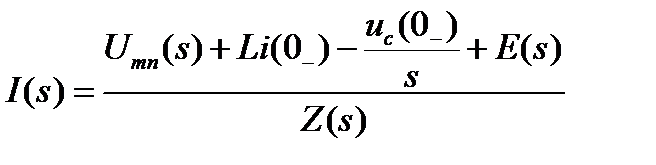
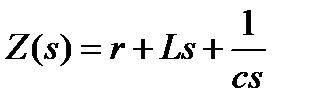
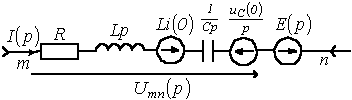
Операторные схемы замещения элементов

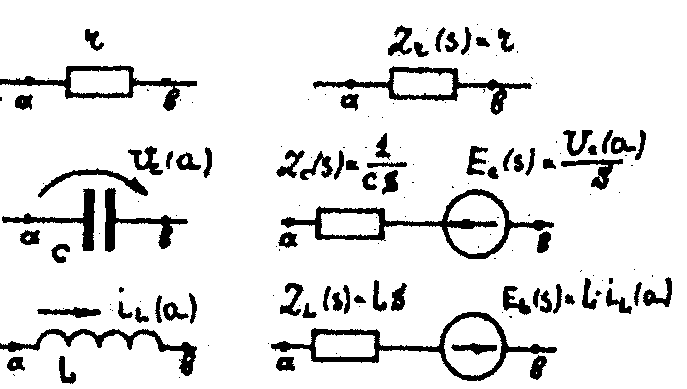
Переход от операторного изображения к оригиналу. Расчет схем с некорректной коммутацией операторным методом.

Переход от изображения к оригиналу.Для определения оригиналов, т.е. исходных токов и напряжений можно воспользоваться либо таблицами, либо применить теорему разложения. Для случая вещественных и различных корней формула разложения имеет вид 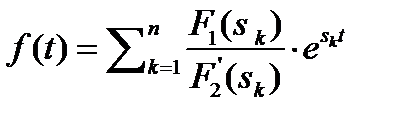(1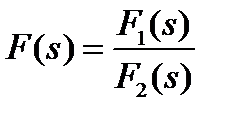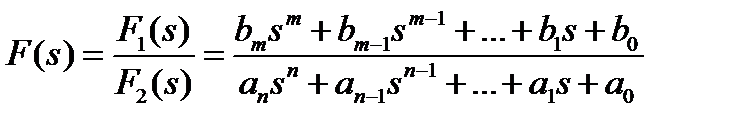), где , где 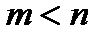, n- число корней,

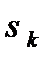- корни характеристического уравнения многочлена знаменателя 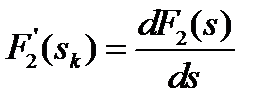при ,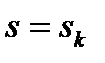

При наличии нулевого корня s=0 имеем 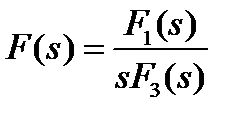и формула разложения принимает вид

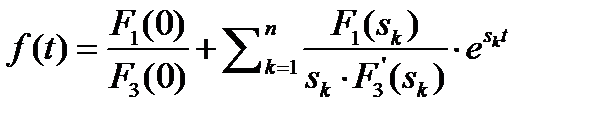Для случая комплекс.-сопряж. корней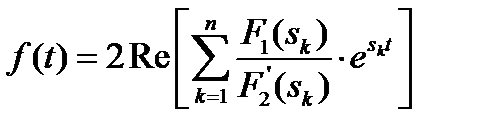

Классификация НЭ

Бывают без ферромагн-ных сердечников, с ними.

Делятся по разным признакам: В зависимости от способности рассеивать электрическую энергию в виде тепла или копить магнитную или эл-кую энергию.

Различают НЭ с симметричной относительно осей координ. (Лампа накаливания, Бареттер-стабилизатор тока в некоторых пределах) и несимметр. (диод) ВАХ. Сопр-е НЭ с несиметр-ой ВАХ зависит от величины и направления тока.

Неуправляемые и управляемые НЭ (Управл. хар-ся семейством кривых параметром которых явл-ся управляющий фактор)

Инерционные и безынерционные: Хар-терной особенностью НЭ при переменном токе явл-ся инерционность, которая определ-ся например изменением сопр-я по действием изменения температуры. Т к нагрев НЭ происходит не сразу, то такие НЭ не реагир на мгновенные всплески тока, а величина сопр-я определ действующим значением тока через НЭ. Если к инерционному сопр-ю приложить U (sin) действующее зн-е которого const, то ток через него также будет синусоидальным; а для безынерц(диод)-не sin.

Сущ-ют НЭ, которые при малых частотах рассматр-ся как безынерц-ые. Изменение сопр-я безынеционных НЭ связано с перераспределением носителей зарядов, которое происходит с большой скоростью. Величина сопр-я в этом случае зависит от мгновенного зн-я U или I на НЭ.

Параметры НЭ

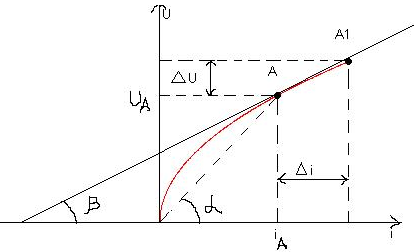В-угол между касат в т. А и i

В нектр т.А режиму в НЭ соответствуют 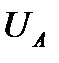и 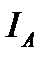. Отношение 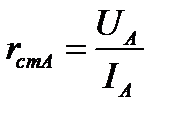наз-ся статистическим сопр-ем НЭ в точке А

В общем случае оно меняется при изменении режима в цепи 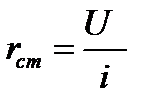. Из графика следует что 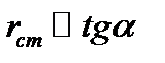, образ-ный кривой соедин. данную точку хар-ки с началом коорд. и положительной осью тока

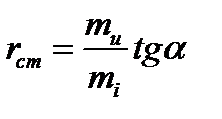, где 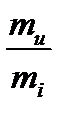-масштаб сопротивл. Для пассивных НЭ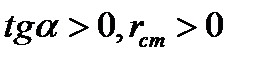

В теории НЭ вводится понятие дифференциального сопр-я: 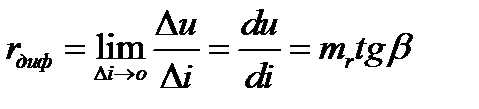. Если U на НЭ получит 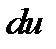то ток вырастет 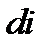. Диф. сопр-е определяет крутизну хар-ки в данной точке. Оно может быть отрицательным. (если в графике есть падения). Приизучении понятий диф и стат сопр-ий полагали что ток и напр-е в схеме меняются с малой скоростью и инерционность НЭ не сказывается на форме ВАХ. При больших скоростях изменения тока и напр-я для расчета инерц НЭ статическими ВАХ пользоваться нельзя, поэтому вводят динамическое сопр-е: 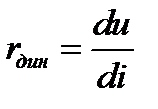Для безынерционных НЭ .

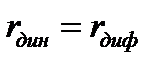ВАХ ветвей содержащие ЭДС

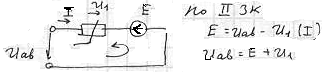а) Направление ЭДС противооложно току

Если последоват с НЭ включен ЭДС то ВАХ участка цепи, содерж-го этот НЭ и источник получается смещением хар-ки НЭ на зн-е ЭДС источника влево или вправо в зависимомти от полярности источника

б) Направление ЭДС совпадает с током

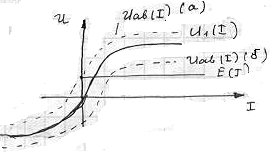
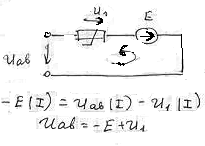
В случае смешанного соединения НЭ производят замену например двух последовательно соединенных эл-тов эквивалентным и далее рассчитывают по одной из вышеприведенных схем.

Метод эквивалентных преобразований Задана разветвл. ЭЦ, треб опр токи в ветвях (задана ВАХ, ист-ники ВАХ)

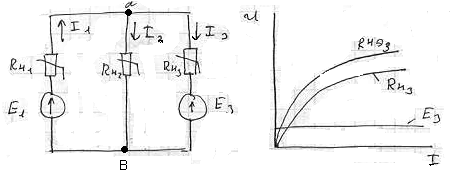
0) Задаемся произ положит напр-ем токов.

1) Строим экв-ную хар-ку третьей ветви.

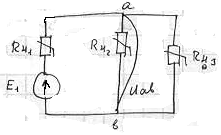
2) Строим экв-ную хар-ку второй и третьей ветвей (парал соед 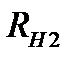и )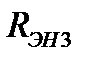

3) Строим экв-ную хар-ку последнего соединения 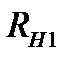и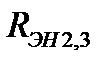

4) Откладываем данное зн-е ЭДС и определ по хар-ке 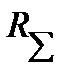ток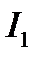

5) По хар-ке 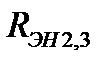и известному току 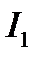определ напряж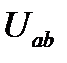

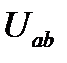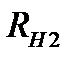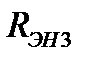6) Зная по хар-кам и определяем ток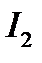и и .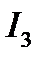

Графический метода расчета простых (с одним источником) нелинейных резистивных цепей постоянного тока при последовательном, параллельном и смешанном соединении элементов. Стабилизатор постоянного напряжения.

Трехфазные цепи: ЭДС, напряжения и токи в системе при соединении фаз генератора и нагрузки звездой, треугольником. Преимущества трехфазной системы.

Трехфазная система ЭДС. Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120 градусов.

Принцип получения трехфазной системы ЭДС. В равномерном магнитном поле с постоянной угловой скоростью ω вращаются три одинаковых жестко скрепленных друг с другом катушки. Плоскости катушек смещены в пространстве друг относительно друга на 120°. В каждой катушке наводится синусоидальная ЭДС одинаковой амплитуды. По фазе ЭДС катушек сдвинуты на 120°.

Преимущества трехфазной системы. Широкое распространение трехфазных систем объясняется главным образом тремя основными причинами: 1) передача энергии на дальние расстояния трехфазным током экономически более выгодна, чем переменным током с иным числом фаз; 2) элементы системы – трехфазный синхронный генератор, трехфазный асинхронный двигатель и трехфазный трансформатор – просты в производстве, экономичны и надежны в работе; 3) система обладает свойствами неизменности значения мгновенной мощности за период синусоидального тока, если нагрузка во всех трех фазах трехфазного генератора одинакова.

2. Операторный метод расчета переходных процессов: преобразование Лапласа; основные свойства преобразования Лапласа; операторное изображение некоторых типовых воздействий.

Переходный процесс – процесс перехода цепи от одного энергетического состояния к другому. Эти процессы вызываются коммутацией эл. цепи. Коммутация – любое изменение параметров цепи, ее конфигурации, а также отключение и подключение источников. Коммутацию считают мгновенной, однако перех. процесс протекает опред. время.

Преобразование Лапласа.

Основные свойства преобразования Лапласа.

Теор. линейности: