ОУМ 8. Теория вероятностей и математическая статистика.

Методы вычислений.

9.1. Классическое и геометрическое определение вероятности.

9.2. Формулы Бернулли, Байеса.

9.3. Интегральная формула Лапласа.

9.4. Основные законы распределения случайных величин (в том числе нормальный закон Гаусса).

9.5. Оценка доверительного интервала с заданной надежностью.

9.6. Критерии достоверной различимости статистических данных, методы Монте-Карло.

9.7. Классические методы вариационного исчисления и их приложения к решению конкретных задач из механики, математической физики: уравнения Эйлера для различных функционалов, методы отыскания оптимального значения функционалов: градиентные методы, метод Ритца, методы оптимального управления (принцип Понтрягина).

9.8. Основные квадратурные формулы (прямоугольников, трапеции, Симпсона), получение оценок точности этих формул.

9.9. Методы Эйлера, Рунге-Кутта решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка: алгоритм решения, скорость сходимости решения соответствующих разностных схем.

9.10. Построение разностных схем для основных типов дифференциальных уравнений в частных производных, доказательство устойчивости и сходимости разностных схем на основе принципа максимума, метода энергетических неравенств.

Литература

1. Лаврентьев М.А., Люстерник А.А. – Курс вариационного исчисления. М., Наука, 1979.

2. Вентцель Б.С. – Теория вероятностей. М., Наука, 1969.

3. Боровков А.А. – Теория вероятностей. М., Наука, 1986.

4. Бахвалов Н.С. – Численные методы. Т. 1,2, М., 1975.

5. Самарский А.А. – Теория разностных схем. М., 1975.

6. Самарский А.А., Гулин А.В. – Численные методы. М., Наука, 1989.

ОУМ 9. Специальные дисциплины

1. Алгебры.

2. Отношение эквивалентности на множестве. Разбиение множеств.

3. Принцип математической индукции. Примеры применения.

4. Теорема об изоморфизме циклических групп порядка n, n Î N.

5. Теорема о разложении конечной абелевой группы в прямое произведение силовских подгрупп.

6. Поле комплексных чисел как расширение поля действительных чисел.

7. Теорема о существовании и единственности простого подполя.

8. Характеристика поля.

9. Теорема о разложении абелевой группы в прямое произведение примерных циклических подгрупп.

10. Теорема об инвариантности максимальных подгрупп нильпотентной группы.

11. Теорема о подгруппе Фраттини конечной группы.

12. Непрерывный гомоморфизм группы (R, +) на группу (R, ·).

13. Непрерывный гомоморфизм группы (R, +) на группу (T, ·).

14. Автоморфизм группы (R, +).

15. Приложения предикатов.

16. Доказательство и вывод на языке предикатов.

17. Аксиоматическое построение теории.

18. Эквивалентность квадратичных форм над полем.

19. Представление нуля квадратичной формой.

20. Бинарные квадратичные формы над полем.

21. Целочисленные бинарные квадратичные формы.

22. Конечные расширения полей.

23. Модули в поле алгебраических чисел.

24. Порядки в поле алгебраических чисел.

25. Дискриминант полного модуля.

26. Полная линейная группа и ее подгруппы.

27. Группы параметрических матриц. Свойства.

28. О применении матричных групп к решению уравнений.

29. Бинарная алгебраическая операция. Свойства.

30. Фундаментальные алгебры.

31. Алгебраические структуры типа решетки.

32. Приложения алгебраических структур.

33. Автоморфизмы групп. Свойства.

34. Регулярное представление групп.

35. Нильпотентные группы автоморфизмов.

36. Матричное представление групп.

37. Ряды централов и коммутантов.

Литература

1. Курош А.Г. Курс высшей алгебры. 1971г.

2. Кострикина А.И. Введение в алгебру. 2000г., 1978г.

3. Курош А.Г. Теория групп. 1967г., 2004г.

4. Холл М. Теория групп. 1962г., 1967г.

5. Huppert B. Endliche Gruppen I. 1967г.

6. А.Х. Журтов, А.А. Цирхов. О конечных группах с независимыми подгруппами. Владикавказ. матем. ж., 12, №4 (2010), 15-20.

7. Л.И. Шидов. О конечных группах с нормализаторным условием. Сиб.матем. ж., т., 21, №6 (1980), 141-145.

8. Ф. Холл. Теория групп. М.: ИЛ, 1982.

9. M. Suzuki. Finite groups in which the centralizer of any element of order 2 is 2- closed. Ann. Math. (2), 82, #2 (1965), 191-212.

10. W. Feit, J.G. Thomson. Solvability of groups of odd order. Pacif. J. Math, 13, #4 (1963), 755-1029.

11. R.A. Wilson. The finite simple groups. Springer, 2009.

12. В.М. Бусаркин, Ю.М. Горчаков. Конечные расщепляемые группы. М., Наука, 1968.

4. Перечень вопросов, определяющих содержание вступительных испытаний

1. Алгоритм Евклида для нахождения НОД и НОК двух чисел.

2. Приложение теории сравнения к признакам делимости чисел.

3. Методы решения систем линейных алгебраических уравнений.

4. Критерий совместности системы линейных алгебраических уравнений.

5. Циклические группы. Изоморфизм циклических групп.

6. Теорема Лагранжа о конечных группах.

7. Теорема о гомоморфизме групп.

8. Делители нуля. Характеристика поля. Свойства.

9. Формулы Виета.

10. Собственные вектора и собственные значения линейного преобразования векторного пространства.

11. Критерий Сильвестра положительной определенности квадратичной формы.

12. Классификация кривых и поверхностей 2-го порядка. Канонический и нормальный вид квадратичной формы.

13. Первая и вторая квадратичные формы.

14. Теорема о дедукции в исчислении высказываний.

15. Теорема о приводимости к нормальным и совершенным формам.

16. Предел функции. Замечательные пределы.

17. Непрерывность функции одной и многих переменных.

18. Теорема о наибольшем и наименьшем значении непрерывных на сегменте функций.

19. Производная, ее геометрический и механический смысл.

20. Полный дифференциал функции многих переменных. Достаточное условие дифференцируемости.

21. Теорема Лагранжа о конечных приращениях для дифференцируемой на сегменте функции.

22. Исследование функции методами дифференциального исчисления.

23. Понятие неявной функции. Условие существования неявной функции одной переменной.

24. Интеграл Римана и его основные свойства.

25. Интеграл по переменному верхнему пределу. Формула Ньютона-Лейбница.

26. Несобственные интегралы. Признаки сходимости.

27. Кратные интегралы. Признак сходимости.

28. Криволинейные интегралы первого и второго рода.

29. Формула Грина.

30. Степенной ряд. Область сходимости степенного ряда.

31. Ряды Фурье. Достаточное условие представимости функции рядом Фурье.

32. Полные метрические пространства (примеры). Пространство Банаха. Принцип сжатых отображений.

33. Интегральные уравнения Вольтерра 1-го и 2-го рода. Резольвента интегрального уравнения Вольтерра второго рода.

34. Компактные множества в метрических пространствах. Критерий компактности пространства непрерывных функций (теорема Арцела).

35. Теорема Фредгольма для компактного оператора.

36. Теорема существования и единственности решения задачи Коши для уравнения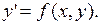

37. Теорема о структуре общего решения обыкновенного линейного дифференциального уравнения.

38. Метод вариации произвольных постоянных. Построение общего решения линейного неоднородного дифференциального уравнения.

39. Нормальная форма системы дифференциальных уравнений.

40. Первые интегралы системы обыкновенных дифференциальных уравнений.

41. Гармонические функции и их свойства.

42. Первая краевая задача для уравнения теплопроводности. Теорема о максимуме и минимуме.

43. Решение первой краевой задачи для прямоугольника методом Фурье.

44. Простейшая задача вариационного исчисления. Формулировка основных лемм и выводов уравнения Эйлера.

45. Аксиоматическое определение вероятности события.

46. Вероятность суммы и произведения событий.

47. Формула полной вероятности.

48. Определение аналитической функции комплексного переменного. Условия Коши-Римана.

49. Теорема Коши об интеграле по замкнутому кусочно-гладкому контуру от аналитической функции комплексного переменного.

50. Интегральная формула Коши.

51. Метод Рунге-Кутта четвертого порядка точности решения задачи Коши для обыкновенного дифференциального уравнения первого порядка.

52. Однородные разностные схемы первой краевой задачи для обыкновенных дифференциальных уравнений второго порядка.

53. Метод сеток решения краевых задач для уравнения теплопроводности. Явные и неявные схемы, погрешность аппроксимации, устойчивость и сходимость.

54. Алгебры.

55. Отношение эквивалентности на множестве. Разбиение множеств.

56. Принцип математической индукции. Примеры применения.

57. Теорема об изоморфизме циклических групп порядка n, n Î N.

58. Теорема о разложении конечной абелевой группы в прямое произведение силовских подгрупп.

59. Поле комплексных чисел как расширение поля действительных чисел.

60. Теорема о существовании и единственности простого подполя.

61. Характеристика поля.

62. Теорема о разложении абелевой группы в прямое произведение примерных циклических подгрупп.

63. Теорема об инвариантности максимальных подгрупп нильпотентной группы.

64. Теорема о подгруппе Фраттини конечной группы.

65. Непрерывный гомоморфизм группы (R, +) на группу (R, ·).

66. Непрерывный гомоморфизм группы (R, +) на группу (T, ·).

67. Автоморфизм группы (R, +).

68. Приложения предикатов.

69. Доказательство и вывод на языке предикатов.

70. Аксиоматическое построение теории.

71. Эквивалентность квадратичных форм над полем.

72. Представление нуля квадратичной формой.

73. Бинарные квадратичные формы над полем.

74. Целочисленные бинарные квадратичные формы.

75. Конечные расширения полей.

76. Модули в поле алгебраических чисел.

77. Порядки в поле алгебраических чисел.

78. Дискриминант полного модуля.

79. Полная линейная группа и ее подгруппы.

80. Группы параметрических матриц. Свойства.

81. О применении матричных групп к решению уравнений.

82. Бинарная алгебраическая операция. Свойства.

83. Фундаментальные алгебры.

84. Алгебраические структуры типа решетки.

85. Приложения алгебраических структур.

86. Автоморфизмы групп. Свойства.

87. Регулярное представление групп.

88. Нильпотентные группы автоморфизмов.

89. Матричное представление групп.

90. Ряды централов и коммутантов.