Vii. интервальное оцениваеие
Пусть X~F(x, q), причём вид функции распределения F(x, q) известен, а параметр q неизвестен (считаем его одномерным). Требуется по выборке указать такой интервал [ 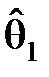 ,
, 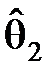 ], который с заданной вероятностью a накрывает неизвестный параметр q:
], который с заданной вероятностью a накрывает неизвестный параметр q:
P{ 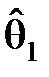 £q£
£q£ 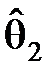 }=a.
}=a.
Сам интервал [ 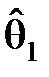 ,
, 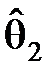 ] называется доверительным, а a – доверительной вероятностью. Концы интервала – функции от выборки:
] называется доверительным, а a – доверительной вероятностью. Концы интервала – функции от выборки:
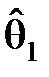 =
= 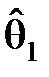 (x1, x2, ¼ , xn),
(x1, x2, ¼ , xn), 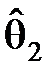 =
= 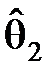 (x1, x2, ¼ , xn)
(x1, x2, ¼ , xn)
и являются случайными величинами. Желательно иметь a близким к единице, а интервал – поменьше. Однако увеличивая a, мы будем получать всё более широкие интервалы и тем самым всё менее информативные интервалы, всё менее интересные. Желательным свойством можно считать условие: 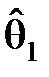 -
- 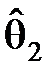
 0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q.
0, тогда при достаточно большом числе наблюдений можно как угодно точно локализовать параметр q.
В качестве a обычно берут числа 0,99, 0,95, 0,9. Выбор доверительной вероятности зависит от практических последствий в случае, когда доверительный интервал не накроет q. При a=0,9 следует ожидать, что в среднем мы будем промахиваться в десятой части всех применений данного доверительного интервала. Если это не страшно, то можно брать a=0,9. Если же нас в этих случаях ждут большие материальные потери или это ведёт к опасностям для человеческой жизни, то такая доверительная вероятность недопустимо мала.
Легко строить доверительный интервал для q, если мы имеем для параметра точечную оценку 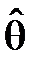 (x1, x2, ¼ , xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения
(x1, x2, ¼ , xn) и хотя бы приближённо знаем закон её распределения. Именно в этом случае по закону распределения 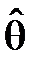 , задавая a, мы можем находить такое e, чтобы
, задавая a, мы можем находить такое e, чтобы
P{| 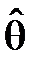 -q|£e}=a.
-q|£e}=a.
Иногда a называют надёжностью оценки, а e – её точностью. Здесь можно переписать неравенство под знаком вероятности в следующем виде:
P{ 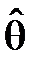 -e£q£
-e£q£ 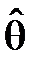 +e}=a,
+e}=a,
и искомый доверительный интервал имеет вид [ 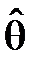 -e,
-e, 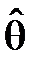 +e] и длину 2e.
+e] и длину 2e.
Разберём несколько задач на построение доверительных интервалов.
1°. Приближённый доверительный интервал для вероятности события.
Пусть имеется событие A и для его вероятности P(A)=p мы хотим построить доверительный интервал, сделав n опытов. Допустим, что в этих опытах событие A наступило m раз.
По интегральной теореме Муавра-Лапласа:
P{a£ 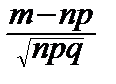 £b}»
£b}» 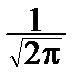
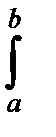
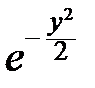 dy.
dy.
Возьмём a=-e, b=e:
P{| 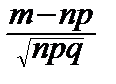 |£e}»
|£e}» 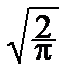
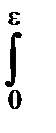
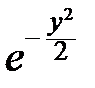 dy=F(e), "e>0.
dy=F(e), "e>0.
Стоящее под знаком вероятности неравенство заменим равносильным:
P{m2-2mnp+n2p2£e2npq}»F(e), "e>0,
или, заменяя q на 1-p:
P{p2(n2+e2n)-p(2mn+e2n)+m2£0}»F(e), "e>0.
Кривая y=p2(n2+e2n)-p(2mn+e2n)+m2 как функция p является параболой.
Пусть её корни p1, p2, причём p1<p2, т. е.
P{p1£p£p2}»F(e), "e>0
и теперь мы можем указать процедуру построения доверительного интервала для p:
a) Задаём доверительную вероятность a.
b) По a находим e из уравнения F(e)=a; корень уравнения легко определяется с помощью таблицы функции Лапласа.
c) Решаем квадратное уравнение p2(n2+e2n)-p(2mn+e2n)+m2=0, находим его корни p1, p2, p1<p2.
d) Искомый приближённый доверительный интервал имеет вид: [p1, p2].
Точность этого интервала зависит от того, достаточно ли мала ошибка при использовании теоремы Муавра-Лапласа, можно ли практически считать, что
m~N(np, 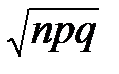 ).
).
2°. Доверительный интервал для параметра a нормального закона при известном s.
Пусть X~N(a, s), причём s известно.
Получаем выборку (x1, x2, ¼ , xn). Среднее выборочное:  ~N(a,
~N(a, 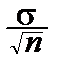 ). Его нормированное уклонение:
). Его нормированное уклонение:
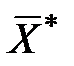 =
= 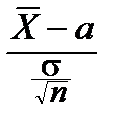 ~N(0, 1).
~N(0, 1).
Поэтому:
P 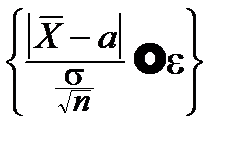 =F(e), "e>0.
=F(e), "e>0.
Заменим неравенство под знаком вероятности равносильным, разрешив его относительно a:
P{  -
- 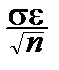 £a£
£a£  +
+ 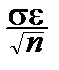 }=F(e)
}=F(e)
и можно сформулировать процедуру построения доверительного интервала для параметра a:
a) Задаём доверительную вероятность a.
b) По a с помощью таблицы функции Лапласа находим e из уравнения F(e)=a.
c)Искомый доверительный интервал имеет вид [  -
- 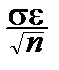 ,
,  +
+ 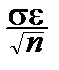 ],
],
Отметим, что длина доверительного интервала сколь угодно мала при больших n: 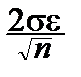
 0.
0.
3°. Доверительные интервалы для параметров нормального закона.
Пусть X~N(a, s) и оба параметра неизвестны. Воспользуемся следующей теоремой о выборочном среднем  и выборочной дисперсии S2 для выборки из нормального закона:
и выборочной дисперсии S2 для выборки из нормального закона:
a)  ~N(a,
~N(a, 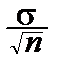 );
);
b)  nS2~c
nS2~c  ;
;
c) 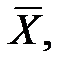 S2 – независимые случайные величины;
S2 – независимые случайные величины;
d) 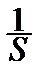 (
(  -a)~Tn-1.
-a)~Tn-1.
Пункт a) этой теоремы очевиден, пункт d) следует из трёх предыдущих.
Действительно,
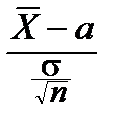 ~N(0, 1);
~N(0, 1); 
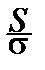 ~cn-1
~cn-1
и из независимости  и S следует, что отношение
и S следует, что отношение 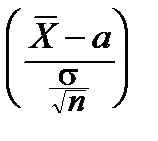 :
: 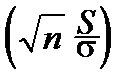 =
= 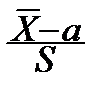 распределено по закону Стьюдента с (n-1) степенями свободы.
распределено по закону Стьюдента с (n-1) степенями свободы.
Пункты b) и c) примем без доказательства. Ограничимся только следующими замечаниями.
В выражении
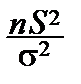 =
= 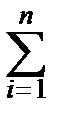
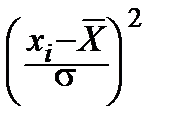
слагаемые – квадраты случайных величин 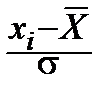 , распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону cn2; однако они связаны линейной зависимостью:
, распределённых по нормальному закону; если бы они были независимыми, то, как мы знаем, сумма была бы распределена по закону cn2; однако они связаны линейной зависимостью:
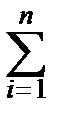
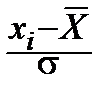 =0.
=0.
Оказывается, это влияет лишь на число степеней свободы у c2, понижая его на единицу. Можно вместо величин (x1, x2, ¼ , xn) ввести с помощью линейного преобразования такие новые величины, которые остаются независимыми и нормальными, причем  и S2 выражаются через различные новые переменные. Это и обеспечивает независимость. К тому же S2 выражается через квадраты ровно (n-1) таких новых величин, что и приводит к c
и S2 выражаются через различные новые переменные. Это и обеспечивает независимость. К тому же S2 выражается через квадраты ровно (n-1) таких новых величин, что и приводит к c  . Осуществление этой программы мы здесь опустим.
. Осуществление этой программы мы здесь опустим.
Теперь построить доверительный интервал для a уже нетрудно:
P{ 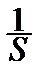 |
|  -a|£e}=2
-a|£e}=2 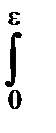 pTn-1(t)dt, "e>0,
pTn-1(t)dt, "e>0,
или
P{  -eS£a£
-eS£a£  +eS}=2
+eS}=2 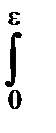 pTn-1(t)dt.
pTn-1(t)dt.
Строим доверительный интервал так:
a) Задаём a.
b) По a из таблицы распределения Стьюдента находим значение e из уравнения 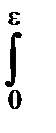 pTn-1(t)dt=
pTn-1(t)dt=  .
.
c) Нужный интервал имеет вид: [  -eS,
-eS,  +eS].
+eS].
Теорема о выборочном среднем позволяет построить доверительные интервалы также для s2и s. Действительно, так как  nS2~c
nS2~c  , то для любых x1, x2, таких, что 0£x1<x2<+¥:
, то для любых x1, x2, таких, что 0£x1<x2<+¥:
P{x1£  nS2£x2}=
nS2£x2}= 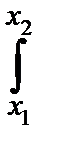
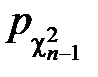 (x)dx.
(x)dx.
Перепишем неравенство под знаком вероятности, решив его относительно s2:
P{ 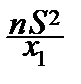 £s2£
£s2£ 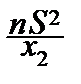 }=
}= 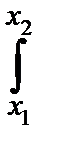
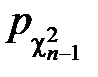 (x)dx.
(x)dx.
|
Обычно выбирают x1, и x2так, чтобы заштрихованные на рисунке площади были равны. Если мы хотим построить интервал с доверительной вероятностью a, то величина каждой из этих площадей, очевидно, равна 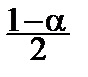 .
.
Процедура построения интервала:
a) Задаём a.
b) Находим x1, и x2по таблицам c2-распределения из уравнений:
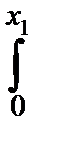
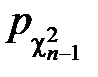 (x)dx=
(x)dx= 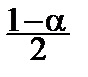 ,
, 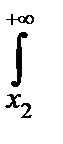
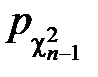 (x)dx=
(x)dx= 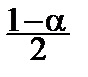 .
.
c) Вычисляем 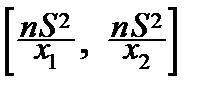 , что и решает нашу задачу.
, что и решает нашу задачу.
Очевидно, для параметра s доверительный интервал выглядит следующим образом:
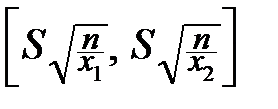 .
.

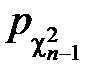 (x)
(x)