I. относительная частота как оценка вероятности

Математическая статистика

ВВОДНЫЕ ЗАМЕЧАНИЯ

В теории вероятностей о вероятностях, законах распределения, параметрах случайных величин говорится как о чём-то данном, известном. Но встаёт вопрос: откуда их взять? Как найти параметры хотя бы приближённо? Как проверить предположение о том, что некоторая случайная величина распределена, например, по нормальному закону?

На эти и подобные им вопросы отвечает математическая статистика, причём информацию для ответов она берёт из наблюдений над случайными событиями и величинами. При этом наблюдения ведутся над реальными объектами и моделями, тогда как теория вероятностей изучает математические модели, в значительной степени идеализированные и абстрагированные. Соотношение между выводами математической теории и поведением реального мира приобретает уже не философский, а практический смысл. Можно сказать, что математическая статистика заведует связями теории вероятностей с внешним миром.

Ниже мы будем рассматривать одну единственную статистическую модель: предполагается, что существует случайная величина X, которую можно наблюдать повторно n раз в независимых опытах. Результатом таких наблюдений оказываются n значений, которые X приняла в n экспериментах: (x₁, x₂, ¼ ¼, x_n), – так называемая выборка, n – объём выборки. На все вопросы о случайной величине X математическая статистика берётся отвечать по выборке.

В каждом опыте мы наблюдаем одну и ту же случайную величину X; все опыты по предположению независимы. Можно считать, что фактически мы наблюдаем n-мерную случайную величину (X₁, X₂, ¼ , X_n) с независимыми компонентами, распределёнными одинаково – по тому же закону, что и X. Выборка (x₁, x₂, ¼ , x_n) есть наблюдённое значение случайной величины (X₁, X₂, ¼ , X_n), выборка – одно из её возможных значений; её можно представить точкой в n-мерном евклидовом пространстве. Всё множество точек, которые могут быть выборками, образует так называемое выборочное пространство. По сути дела выборка – элементарное событие, а выборочное пространство – пространство элементарных событий W. Часто смотрят на выборку (x₁, x₂, ¼ , x_n) как на случайную величину и не вводят особого обозначения (X₁, X₂, ¼ , X_n) для случайной величины.

Если X~N(a, s), то выборочным пространством оказывается всё евклидово пространство R_n. Если X~P(l), то выборочное пространство совпадает с целочисленной решёткой главного координатного угла. Если X~R(0, 1), то W – единичный n-мерный куб.

Пусть X~F(x, q): F(x, q) – функция распределения случайной величины X. Тогда совместная функция распределения выборки:

F(x₁, x₂, ¼ , x_n)= 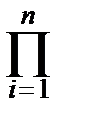F(x_i, q).

Если X имеет плотность вероятности p(x, q), то совместная плотность вероятности выборки равна

p(x₁, x₂, ¼ , x_n)= 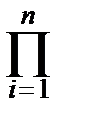p(x_i, q).

Познакомимся с важнейшими задачами математической статистики и с их статистическими решениями.

V. ГРУППИРОВКА НАБЛЮДЕНИЙ

Если объём выборки очень велик, то обрабатывать весь массив собранных данных бывает иногда затруднительно. С целью облегчить вычислительную работу в таких случаях производят так называемую группировку наблюдений. Она бывает также необходима для некоторых статистических процедур.

Представим выборку (x₁, x₂, ¼ , x_n) в виде вариационного ряда: y₁£y₂£
£¼£y_n. Величина y_n-y₁ называется размахом выборки. Разобьём отрезок [y₁, y_n] на N равных частей длины D= .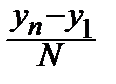

Поскольку неизбежно округление данных, следует договориться о концах интервалов: разбиваем весь отрезок [y₁, y_n] на отрезки

D_k=[x_k^o- 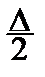, x_k^o+ ),

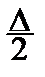где x_k^o– середина k-ого полузакрытого интервала. При таком разбиении последний интервал берём в виде

D_N=[x_N^o- 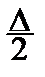, x_N^o+ ].

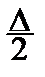Обозначим через m_kчисло наблюдений, попавших в k-й интервал D_k. Числа  x₁^o<x₂^o<¼<x_N^o называют интервальным вариационным рядом, m_k– приписанные этим точкам частоты.

В принципе, можно строить интервальный вариационный ряд, производя, если это нужно, разбиение и на неравные интервалы.

Вся дальнейшая работа (например, построение эмпирической функции распределения, оценки и т. д.) осуществляется уже с интервальным вариационным рядом. При этом нужно не забывать, что группировка вносит в статистические вычисления дополнительную ошибку – ошибку на группировку.

Число интервалов N выбирают так, чтобы частоты m_kбыли достаточно велики, а само число N не слишком велико.

Разбиение на неравные интервалы производят в том случае, если на оси x есть области очень бедные попавшими туда наблюдениями.

Математическая статистика

ВВОДНЫЕ ЗАМЕЧАНИЯ

В теории вероятностей о вероятностях, законах распределения, параметрах случайных величин говорится как о чём-то данном, известном. Но встаёт вопрос: откуда их взять? Как найти параметры хотя бы приближённо? Как проверить предположение о том, что некоторая случайная величина распределена, например, по нормальному закону?

На эти и подобные им вопросы отвечает математическая статистика, причём информацию для ответов она берёт из наблюдений над случайными событиями и величинами. При этом наблюдения ведутся над реальными объектами и моделями, тогда как теория вероятностей изучает математические модели, в значительной степени идеализированные и абстрагированные. Соотношение между выводами математической теории и поведением реального мира приобретает уже не философский, а практический смысл. Можно сказать, что математическая статистика заведует связями теории вероятностей с внешним миром.

Ниже мы будем рассматривать одну единственную статистическую модель: предполагается, что существует случайная величина X, которую можно наблюдать повторно n раз в независимых опытах. Результатом таких наблюдений оказываются n значений, которые X приняла в n экспериментах: (x₁, x₂, ¼ ¼, x_n), – так называемая выборка, n – объём выборки. На все вопросы о случайной величине X математическая статистика берётся отвечать по выборке.

В каждом опыте мы наблюдаем одну и ту же случайную величину X; все опыты по предположению независимы. Можно считать, что фактически мы наблюдаем n-мерную случайную величину (X₁, X₂, ¼ , X_n) с независимыми компонентами, распределёнными одинаково – по тому же закону, что и X. Выборка (x₁, x₂, ¼ , x_n) есть наблюдённое значение случайной величины (X₁, X₂, ¼ , X_n), выборка – одно из её возможных значений; её можно представить точкой в n-мерном евклидовом пространстве. Всё множество точек, которые могут быть выборками, образует так называемое выборочное пространство. По сути дела выборка – элементарное событие, а выборочное пространство – пространство элементарных событий W. Часто смотрят на выборку (x₁, x₂, ¼ , x_n) как на случайную величину и не вводят особого обозначения (X₁, X₂, ¼ , X_n) для случайной величины.

Если X~N(a, s), то выборочным пространством оказывается всё евклидово пространство R_n. Если X~P(l), то выборочное пространство совпадает с целочисленной решёткой главного координатного угла. Если X~R(0, 1), то W – единичный n-мерный куб.

Пусть X~F(x, q): F(x, q) – функция распределения случайной величины X. Тогда совместная функция распределения выборки:

F(x₁, x₂, ¼ , x_n)= 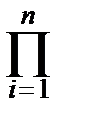F(x_i, q).

Если X имеет плотность вероятности p(x, q), то совместная плотность вероятности выборки равна

p(x₁, x₂, ¼ , x_n)= 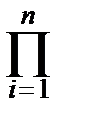p(x_i, q).

Познакомимся с важнейшими задачами математической статистики и с их статистическими решениями.

I. ОТНОСИТЕЛЬНАЯ ЧАСТОТА КАК ОЦЕНКА ВЕРОЯТНОСТИ

Пусть имеется событие A, вероятность которого P(A)=p – неизвестна, и мы хотим найти её хотя бы приблизительно. Из курса теории вероятностей ответ нам известен: хорошим приближением для вероятности является относительная частота события. Если в n независимых опытах событие A произошло m раз, то P(A)» 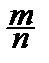. При этом:

1.В среднем мы не ошибаемся: M( 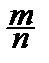)»p.

Это свойство оценки называется несмещённостью.

2. Дисперсия оценки как угодно мала при достаточно большом числе опы­тов: D( 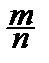)= 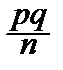®0 при n®¥.

Дисперсия играет роль среднего квадрата ошибки.

3. Вероятность заметных отклонений относительной частоты от вероятности мала, поскольку по закону больших чисел Бернулли:

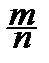
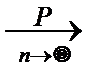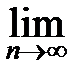p Û  P{| 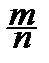-p|<e}=1 для "e>0.

Это свойство оценки называется состоятельностью. Оно может быть усилено, поскольку по закону больших чисел Бореля:

P{ 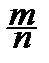®p}=1.

Итак, относительная частота – несмещённая, состоятельная оценка для вероятности со сколь угодно малой среднеквадратической ошибкой.

Решение I задачи, таким образом, нам известно, и оно послужит нам удобным образцом для более сложных задач.

Разумеется, нужно понимать, что полученный ответ точно укладывается в рамки той единственной модели, которую мы взялись изучать в математической статистике.

Можно считать, что мы имеем здесь дело с биномиальной случайной величиной X, а выборка состоит из одного наблюдения m. Либо можно считать, что мы имеем дело здесь со случайной величиной Х=

1, если событие A произошло,
0, если событие A не произошло.

Очевидно, X – дискретная случайная величина с двумя возможными значениями 1 и 0, а вероятности этих значений p и q=1-p. Мы уже встречались с подобной величиной и выяснили, что MX=p, DX=pq.

Соответственно выборка (x₁, x₂, ¼ , x_n) состоит из m единиц и n-m нулей, выборочное пространство состоит из вершин n-мерного единичного куба, и

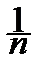(x₁+x₂+¼+x_n)= ,

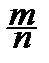так что ответ мы действительно получаем в терминах выборки:

p=P(A)» 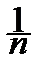(x₁+x₂+¼+x_n)= = .

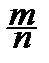II. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
КАК ОЦЕНКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ

Пусть функция распределения случайной величины X неизвестна. Обозначим её F(x). Требуется хотя бы приблизительно её найти. Получим выборку (x₁, x₂, ¼ , x_n) и по ней построим так называемую эмпирическую функцию распределения:

F_n(x)= 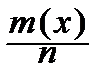, -¥<x<+¥,

где m(x) – число наблюдений в выборке, оказавшихся меньше x.

Убедимся в том, что эмпирическая функция распределения – хорошее при­ближение для F(x).

Расположим наблюдения в порядке возрастания, причём повторяющиеся наблюдения выпишем лишь один раз: получим возрастающую последовательность y₁<y₂<¼<y_r, называемую вариационным рядом; члены её называются порядковыми статистиками. Так, y₁= 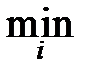x_i – минимальная порядковая статистика – первый член вариационного ряда; y_r= 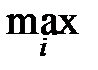x_i – максимальная порядковая статистика – последний член вариационного ряда. Пусть частота значения y_iравна m_i. Тогда очевидно:

0, если x£y₁,
F_n(X)= 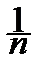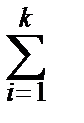m_i, если y_k<x£y_k+1, k=1, 2, ¼ , r-1,
1, если x>y_r.

Fn(x)=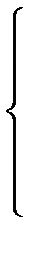

В частности, если все наблюдения различны (так будет, например, почти наверное для непрерывной случайной величины X), то вариационный ряд состоит из n порядковых статистик и

0, если x£y₁,
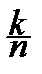, если y_k<x£y_k+1, k=1, 2, ¼ , n-1,
1, если x>y_n.

Очевидно, F_n(x) – ступенчатая неотрицательная монотонная функция, имеющая разрывы в точках y_i, где она совершает скачки величины 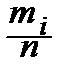. Она обладает всеми свойствами функции распределения и задаёт закон распределения дискретной случайной величины с возможными значениями y_iи вероятностями 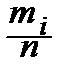. Она и решает нашу задачу приближённого описания F(x).

Действительно, рассмотрим событие A={X<x}.

Его вероятность P(A)=P{X<x}=F(x), его абсолютная частота m=m(x), его относительная частота равна F_n(x), и мы свели рассматриваемую II задачу к I, ответ на которую мы уже знаем.

Следовательно, для любого x эмпирическая функция распределения F_n(x) приближённо равна F(x), причём F_n(x) обладает следующими свойствами:

1. MF_n(x)=F(x), т. е. F_n(x) – несмещённая оценка F(x);

2. DF_n(x)= 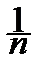{F(x)[1-F(x)]} 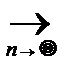0;

3. F_n(x) 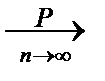F(x) Û  P{|F_n(x)-F(x)|<e}=1, "e>0. И даже:

P{F_n(x) 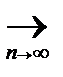F(x)}=1 – состоятельность оценки F_n(x).

Итак, эмпирическая функция распределения F_n(x) для любого x – несмещённая, состоятельная оценка F(x) со сколь угодно малой среднеквадратической ошибкой.

III. СРЕДНЕЕ ВЫБОРОЧНОЕ КАК ОЦЕНКА
МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

Требуется по выборке (x₁, x₂, ¼ , x_n) оценить (т. е. приближённо найти) MX. Ответ нам уже известен: хорошим приближением для среднего значения случайной величины является среднее арифметическое наблюдений:

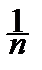
MX» = 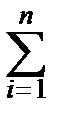x_i.

Очевидно, мы можем пользоваться теоремами о среднем арифметическом, применяя их к нашей выборке – последовательности одинаково распределённых независимых случайных величин.

Будем предполагать, что X имеет MX =a, и DX=s².

1. В среднем мы не ошибаемся, поскольку 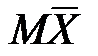=a (имеет место несмещённость).

2. Среднеквадратическая ошибка приближения как угодно мала при n®¥, поскольку 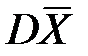 = 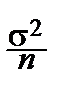®0.

3. подчиняется закону больших чисел Чебышёва:

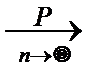a, т. е.  P{| -a|<e}=1, "e>0,

следовательно имеет место состоятельность.

В статистике принято называть средним выборочным. Таким образом, среднее выборочное – несмещённая состоятельная оценка для математического ожидания со сколь угодно малой дисперсией при достаточно большом объёме выборки.