Дискретные модели в пространстве состояния

1. Переход от разностного уравнения к уравнениям состояния

Рассмотрим дискретную ПФ:

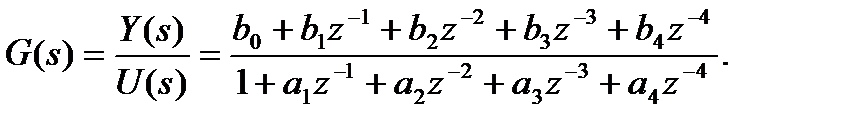
где оператор z^-1 означает задержку на один такт.

Этой ПФ соответствует разностное уравнение

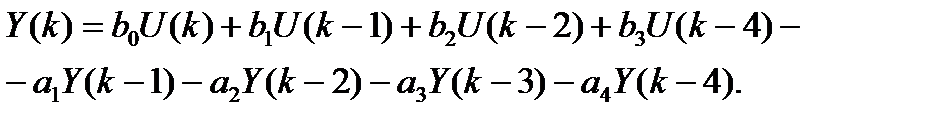
и граф, показанный на рис. 4.

z–1

U(s)

b4

z–1

x1

x4

Y(s)

–a1

x2

z–1

z–1

x3

–a2

–a3

–a4

b1

b2

b3

b0

Рис. 4. Сигнальный граф для дискретной ПФ

Выбирая в качестве переменных состояния выходы элементов задержки, можно записать

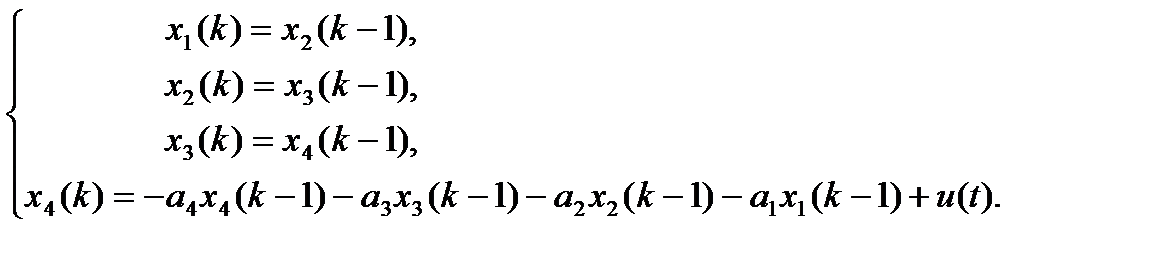
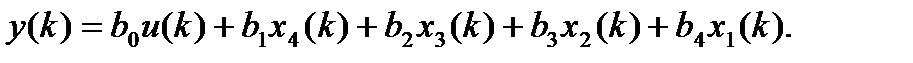
В матричной форме

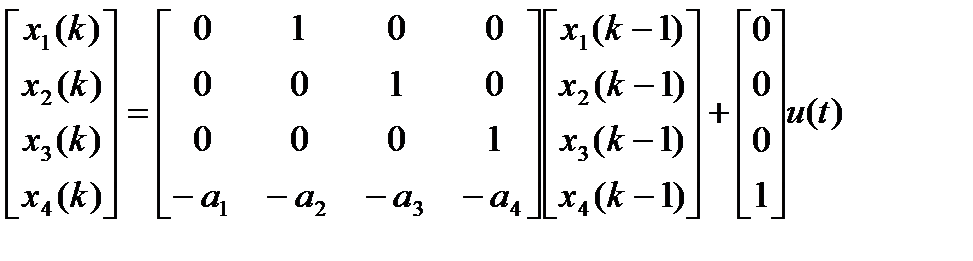
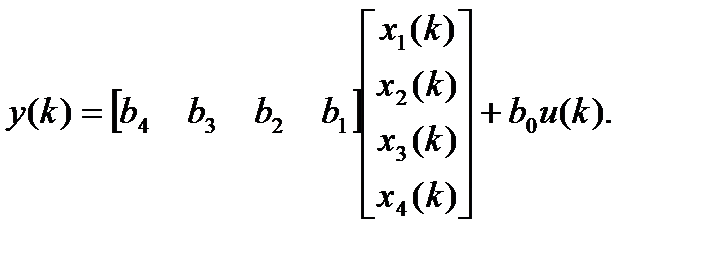
Пример. Пусть имеется дискретная ПФ

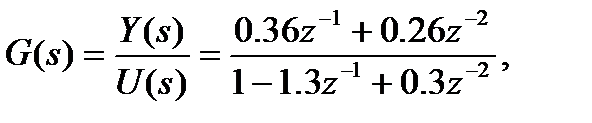
И соответствующее разностное уравнение

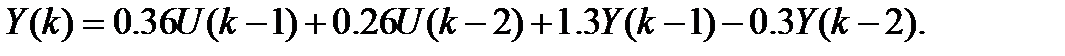
Сигнальный граф этой системы показан на рис. 2. Применяя к нему формулу Мейсона, можно получить исходную дискретную ПФ.

Примем выход каждого элемента задержки за переменную состояния x₁(k) и x₂(k), тогда входы элементов задержки равны x₁(k+1) и x₂(k+1)

U(z)

0.26

x1

Y(z)

z–1

x2

1.3

0.36

z–1

–0.3

Рис. 2

Модель в переменных состояния приобретает вид:

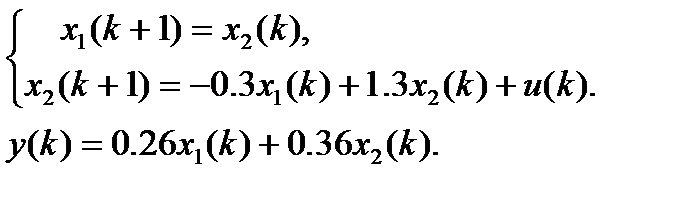
В матричной форме

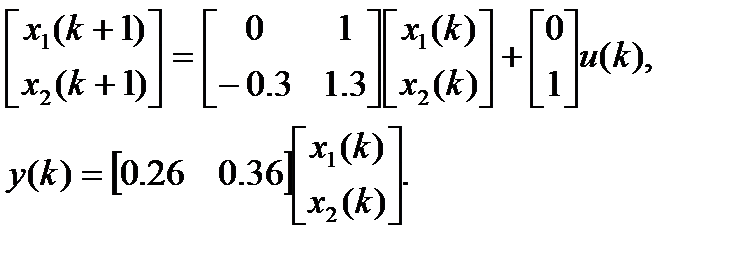
Таким образом, модель дискретной системы в пространстве состояний можно получить, используя либо разностное уравнение, либо дискретную ПФ.

Переход от уравнений состояния к передаточной функции.

Рассмотрим линейную стационарную систему

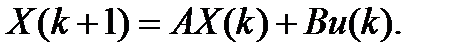
Применяя z-преобразование, имеем

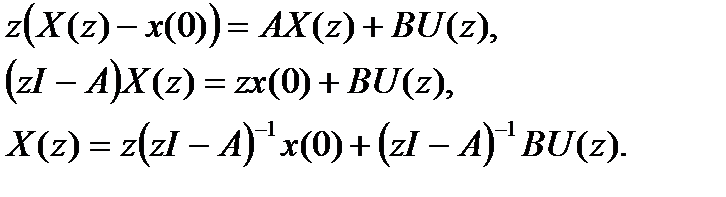
2. Получение дискретного представления из непрерывного

Рассмотрим скалярное дифференциальное уравнение 1-го порядка

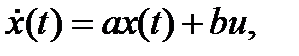
Где a и b – числа, x и u – скалярные переменные.

Рассмотрим преобразование этого уравнения по Лапласу:

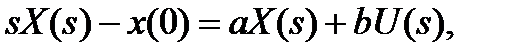
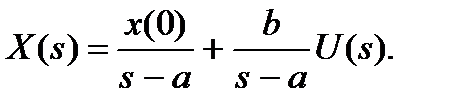
Обратное преобразование Лапласа этого уравнения дает

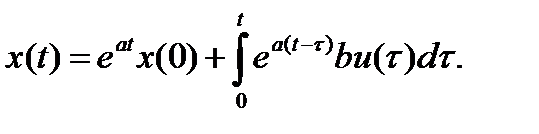
Это формула обобщается для системы произвольного вида

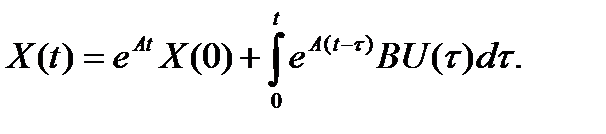
Рассмотрим движение объекта на интервале квантования T, используя непрерывное описание:

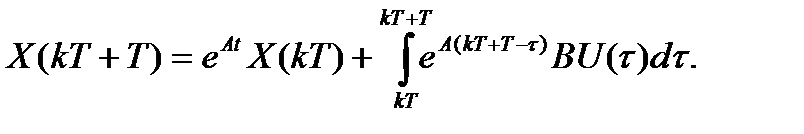
Поскольку на интервале квантования T управление не изменяется: U(t) = U(kT), можно записать:

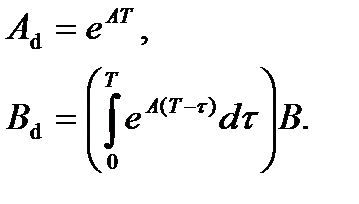
(При записи последней формулы можно считать kT = 0).

Таким образом

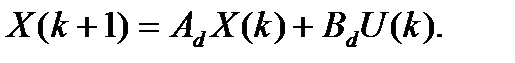
Выход цифровой системы можно рассчитывать по формуле:

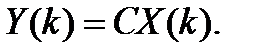
Поскольку время срабатывания АЦП и ЦАП намного меньше периода квантования, и его можно не учитывать.

Дискретная система в пространстве состояний описывается структурой, приведенной на рис. 4:

Bd

ò

C

Ad

U(k)

X(k)

X(k+1)

Y(k)

Рис. 4. Дискретная форма уравнений состояния

Методика синтеза цифровых модальных регуляторов принципиально не отличается от методики синтеза непрерывных модальных регуляторов.

Рассматривая уравнения состояния в дискретной форме, можно обосновать критерий управляемости.

Пусть задано описание стационарной дискретной системы:

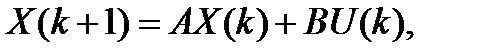
где A - матрица размером (n× n), B - матрица размером (n× 1).

Можно записать выражение:

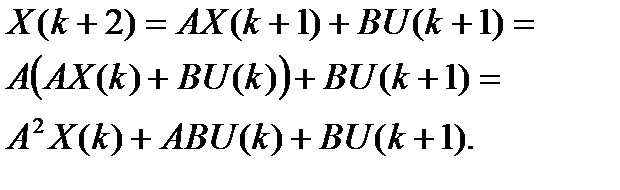
Аналогично:

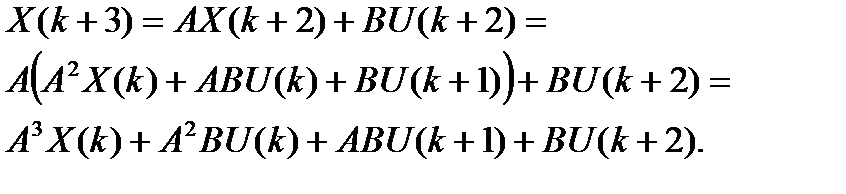
Окончательно:

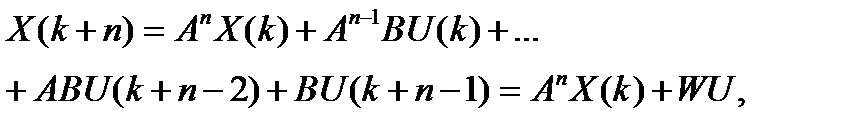
где

W = [A^n-1B; A^n-2B; … A²B; AB; B],

U = [U(k) U(k + 1) … U(k + n – 2) U(k + n – 1)]^T

Если матрица управляемости W невырожденная (несингулярная), то из выражения

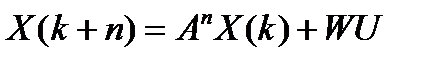
следует

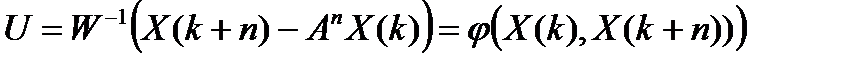
Таким образом, для полностью управляемого объекта можно рассчитать управление, рассматривая инверсную динамику объекта.

Пример. Объект управления задан матрицами:

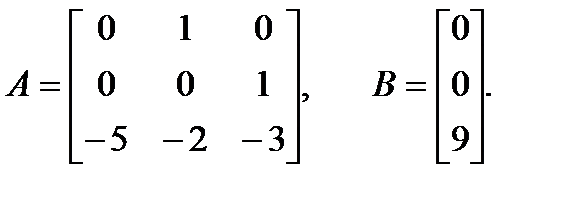
Матрица управляемости

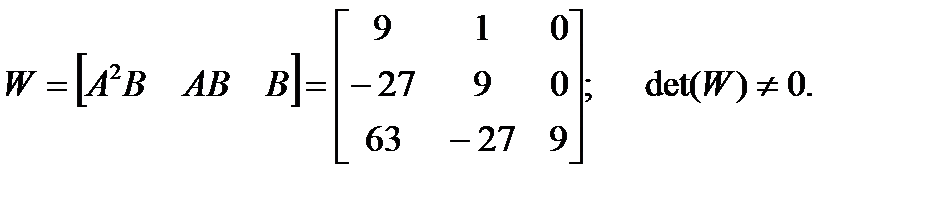
Сигнал управления