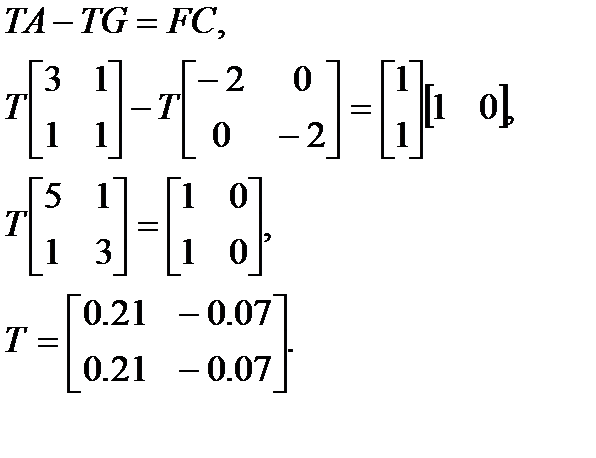Выбор полюсов желаемой замкнутой системы

На первом этапе синтеза модального регулятора необходимо задать расположение полюсов замкнутой системы.

Выбирать положение полюсов можно, опираясь на корневые оценки качества системы. Один из возможных подходов заключается в обеспечении одинаковости всех корней характеристического уравнения. Каждый корень λ должен быть отрицательным, а величина его модуля λ₀ определяется требованиями к быстродействию. Левая часть характеристического уравнения обращается в бином Ньютона (s + λ₀)ⁿ, разворачивая который, можно получить стандартные значения коэффициентов характеристического уравнения. Биномиальные стандартные формы для систем до четвертого порядка имеют вид:

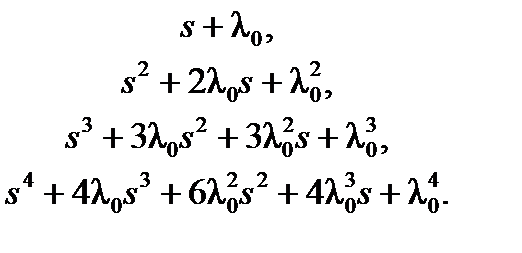
При таком подходе обеспечивается апериодичность переходного процесса. Чем больше λ₀, тем меньше время переходного процесса.

Существуют и другие стандартные формы, например форма Баттерворта, в соответствии с которой корни должны располагаться в левой полуплоскости на окружности радиуса λ₀ на одинаковых угловых расстояниях друг от друга (рис. 2.5).

Re

Im

-λ0

Рис. 2.5. Распределение Баттерворта для системы 4-го порядка

Стандартные формы Баттерворта для систем до четвертого порядка имеют вид:

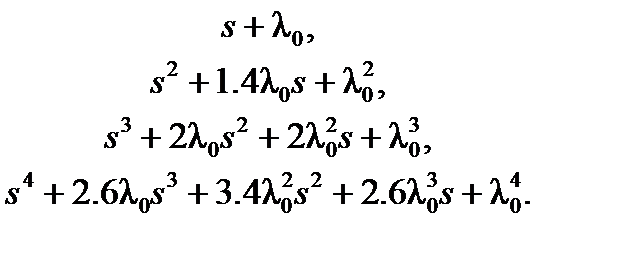
Полином Баттерворта обеспечивает заданное время переходного процесса и перерегулирование в пределах 15%.

Пример 2.11. Рассмотрим задачу модального управления двигателем постоянного тока (ДПТ), упрощенная схема которого приведена на рис. 2.6.

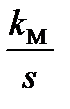kИЭ

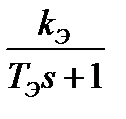ω

Uy

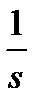Uя

ΔU

IЯ

φ

ke

ДПТ

Рис. 2.6. Блок-схема двигателя постоянного тока

На рис. 2.6 использованы обозначения: U_y – управляющее напряжение; U_я – входное напряжение ДПТ; k_ИЭ – коэффициент передачи исполнительного элемента (транзисторного преобразователя); k_Э – коэффициент передачи электрической части двигателя; T_Э – постоянная времени электрической части двигателя; k_М – коэффициент передачи механической части двигателя; k_е – конструктивный коэффициент ДПТ; ω– частота вращения ротора; φ– угол поворота ротора.

Примем следующие параметры ДПТ: k_ИЭ = 20; k_Э = 5; T_Э = 0,2; k_М = 1,2; k_е = 0,5.

Тогда передаточная функция системы приобретает вид:

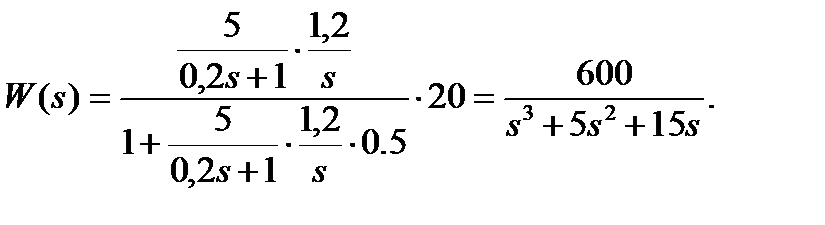
Далее для описания желаемой системы выберем стандартный биномиальный полином

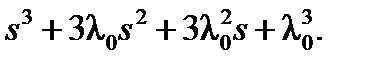
Поскольку все полюса располагаются в одной точке, здесь легко оценить время переходного процесса в системе

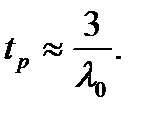
Выбирая, например t_p = 0.5, получаем λ₀ = 6. Стандартный полином приобретает вид

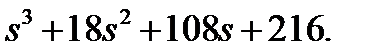
Приравнивая нулю, получаем характеристическое уравнение желаемой замкнутой системы.

Запишем далее уравнения состояния

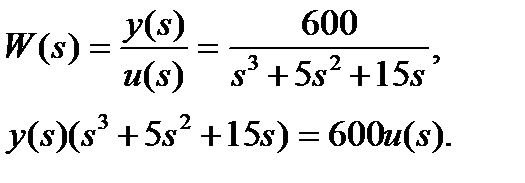
Таким образом,

b₀ = 600, a₃ = 1, a₂ = 5, a₁ = 15, a₀ = 0.

Каноническая форма управляемости приобретает вид:

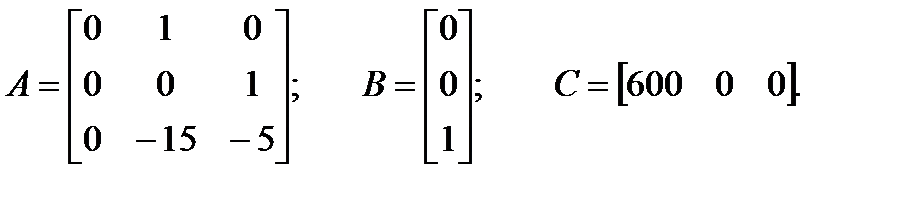
Каноническая форма матрицы желаемой замкнутой системы

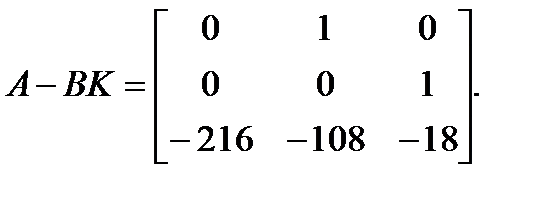
Таким образом, коэффициенты обратной связи:

k₁ = 216,

k₂ = 108 – 15 = 93,

k₃ = 18 – 5 = 13.

Рассчитаем масштабирующий коэффициент для этой системы

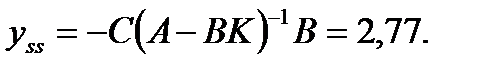
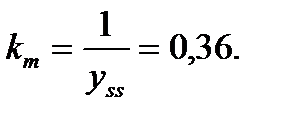
Следует заметить, что теоретически может быть рассчитана любая обратная связь, помещающая полюса замкнутой системы в любое желаемое положение. Однако на практике существуют естественные ограничения на значения сигнала управления и возможные состояния объекта. Поэтому полюса желаемой системы (с обратной связью) следует располагать на комплексной плоскости как можно ближе к полюсам исходной системы.

Наблюдающие устройства

Метод модального управления предполагает, что все компоненты вектора состояния X могут быть измерены, но на практике некоторые компоненты могут быть неизвестны по одной из двух причин:

- измерительных приборов может быть недостаточно;

- некоторые компоненты вектора X могут не иметь физического смысла.

Однако если система является наблюдаемой, то все компоненты вектора X могут быть восстановлены по наблюдениям вектора Y.

Иначе говоря, если система наблюдаемая, то все компоненты вектора состояния вносят свой вклад в выходной сигнал системы.

В настоящее время известны два подхода косвенного определения компонент вектора состояния управляемого объекта, недоступных прямому измерению. Это фильтр Калмана и наблюдающее устройство Люинбергера.

При использовании фильтров Калмана детерминированный подход к рассмотрению анализируемой системы автоматического управления заменяется стохастическим. Областью применения таких наблюдающих устройств являются в основном системы управления сложными электромеханическими устройствами.

При анализе детерминированных механических систем задача оценки всех переменных состояния управляемого объекта может быть решена с помощью более простого устройства, называемого наблюдающим устройством Люинбергера. Входными сигналами для этого устройства служат доступные измерению выходные координаты объекта, а также поступающие на него входные воздействия.

Наблюдающие устройства Люинбергера представляют собой динамическую систему, которая является моделью объекта:

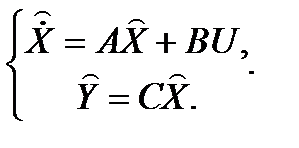
где 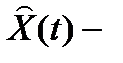оценка состояния объекта, 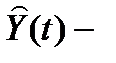оценка выхода.

Рассмотрим ошибку состояния и выхода:

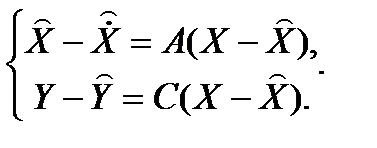
Если начальное состояние объекта и модели совпадают, и модель адекватна объекту, то можно полагать в любой момент времени, что

.

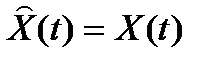Общая структура системы управления с наблюдателем показана на рис. 2.7.

Регулятор

Объект

Наблюдатель

G(t)

U(t)

X(t)

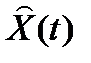Y(t)

Y(t)

Измеритель

Рис. 2.7. Система управления с наблюдателем

Однако практически добиться полной адекватности объекта и модели невозможно, трудно добиться и полного равенства начальных условий. Поэтому на практике можно рассчитывать лишь на выполнение условия

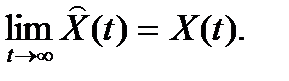
Подобным свойством обладают так называемые асимптотические наблюдающие устройства.

Асимптотическое наблюдающее устройство использует обратную связь по ошибке восстановления вектора состояния, так что работа наблюдающего устройства описывается уравнением

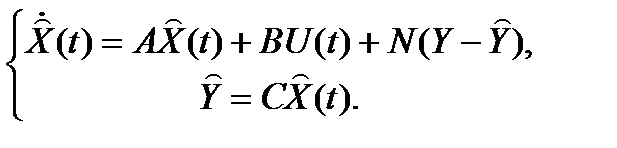
где N – матрица параметров наблюдающего устройства.

Можно записать

.

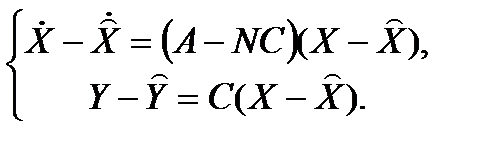Если ввести обозначение для ошибки по состоянию

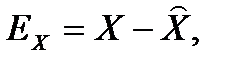
то получаем

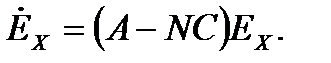
Таким образом, если собственные числа матрицы A – NC имеют отрицательную вещественную часть, то с течением времени ошибка состояния уменьшиться до нуля. Соответственно, при синтезе наблюдателя нужно выбрать положение корней характеристического уравнения:

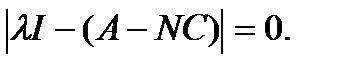
Рассмотрим влияние наблюдателя на динамику системы с обратной связью. Система с наблюдателем описывается уравнениями

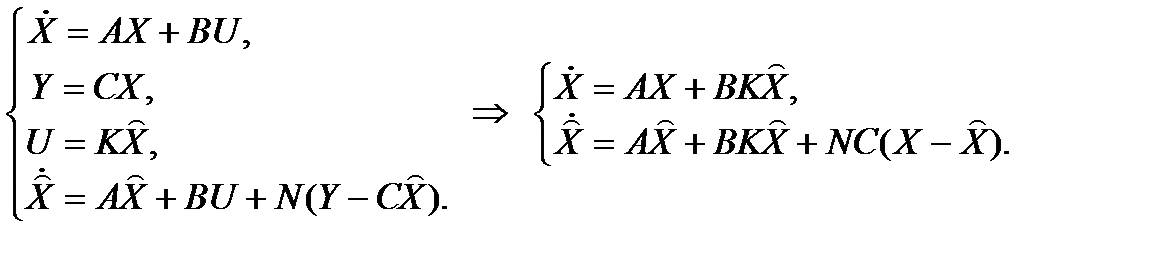
Структурная схема системы с наблюдающим устройством показана на рис. 2.9.

B

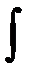C

A

X(t)

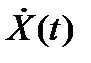Y(t)

N

g(t)

B

C

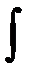A

K

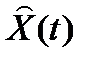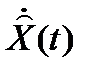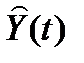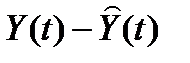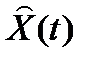Регулятор

Наблюдатель

Объект

U(t)

Рис. 2.9. Система с наблюдающим устройством

Рассмотрим систему

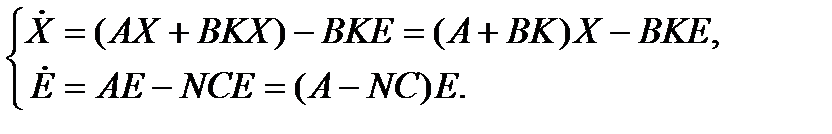
Таким образом, уравнения динамики системы с наблюдающим устройством можно записать в матричной форме

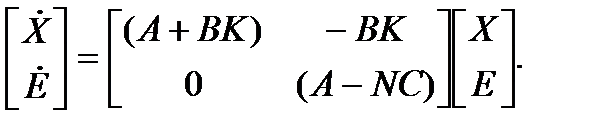
Характеристическое уравнение этой системы имеет вид:

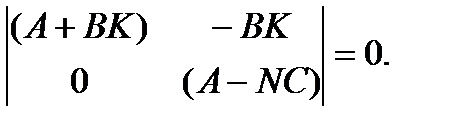
Собственные значения блочной треугольной матрицы совпадают с собственными значениями диагональных блоков

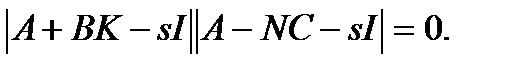
Это уравнение имеет 2n корней, из которых n корней заданы условиями модального синтеза и еще n являются корнями наблюдателя. Таким образом, оказывается, что параметры наблюдателя и параметры регулятора могут рассчитываться независимо.

Понятно, что процессы в наблюдателе должны протекать более быстро, чем переходный процесс в системе. Эмпирически установлено, что наблюдатель должен обладать быстродействием, в 2 - 4 раза превышающим быстродействие системы.

При синтезе наблюдателя удобно использовать каноническую форму наблюдаемости.

Пример Рассмотрим объект 3-го порядка

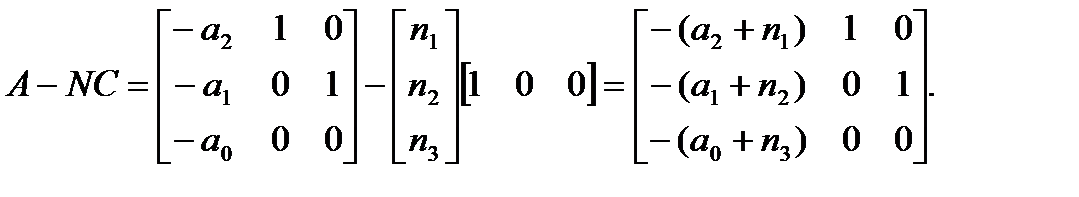
Характеристическое уравнение принимает вид:

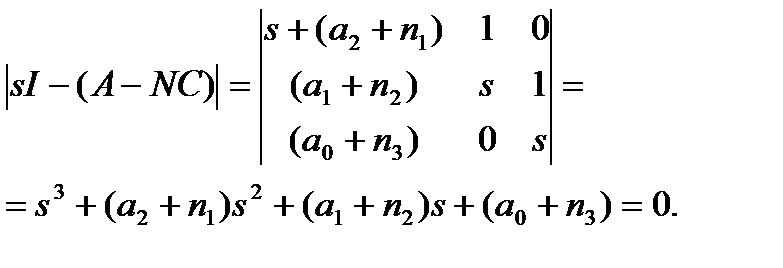
Далее надо рассмотреть характеристический полином желаемой замкнутой системы

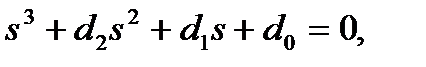
и, приравняв коэффициенты при одинаковых степенях s, найти параметры наблюдателя:

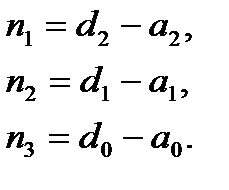
Пример 2.12. Объект управления задан матрицами в канонической форме наблюдаемости

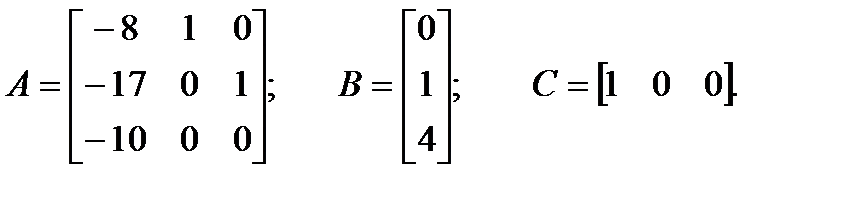
Требуется построить наблюдающее устройство.

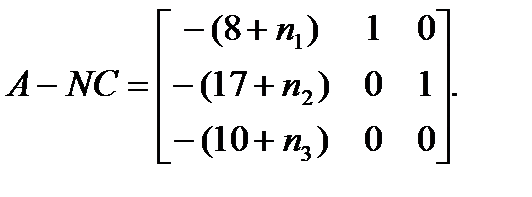
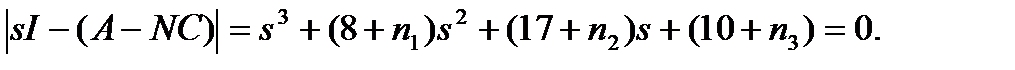
Допустим, что выбран следующий желаемый характеристический полином

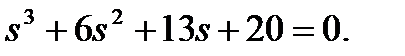
Тогда параметры наблюдателя равны:

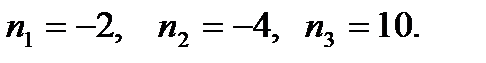
В рассмотренном примере синтез наблюдателя выполнен методом модального управления.

Второй способ синтеза наблюдателя – это собственно синтез наблюдателя Люенбергера.

Введём n-мерный вектор состояния наблюдателя V, связанный с X соотношением

,

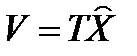где T – не особая матрица размерности n×n. Из системы уравнений

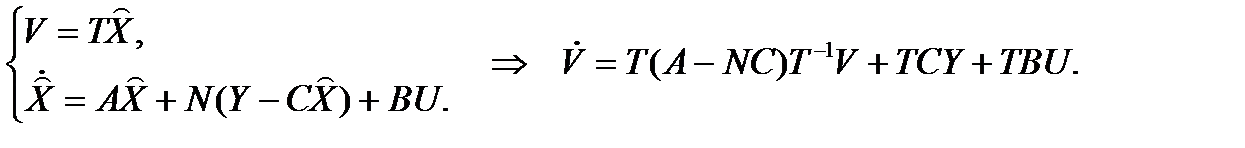
Введем обозначение

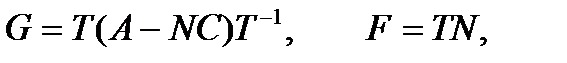
где N – неизвестная матрица.

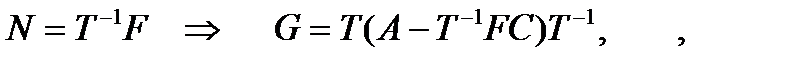
откуда следует

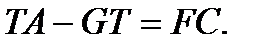
Таким образом, наблюдатель Люенбергера описывается системой уравнений

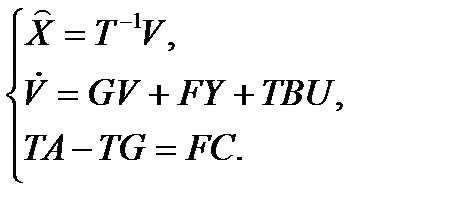
Пример.

Пример 2.22. Объект управления задан уравнениями в пространстве состояний:

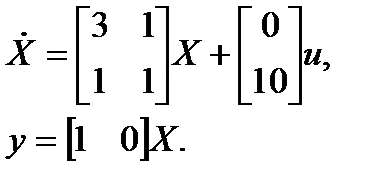
Требуется построить наблюдатель Люинбергера.

На первом шаге проверяется наблюдаемость объекта:

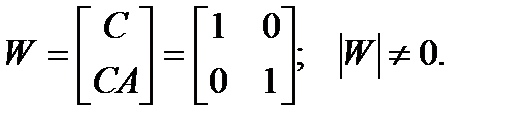
Допустим, что при модальном синтезе выбраλно положение полюсов замкнутой системы: λ₁ = λ₂ = –1. Матрица G описывает динамику наблюдателя, она должна иметь собственные числа, находящиеся левее на комплексной плоскости. Например

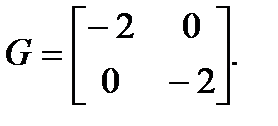
Матрица F выбирается из условий управляемости наблюдателя. Например:

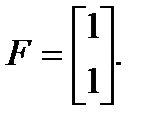
Затем необходимо решить уравнение: