Оценка адекватности полученной парной регрессии

Процедура интервального прогнозирования значений объясняющей переменной используется для проверки адекватности оцененной модели.

Алгоритм проверки адекватности построенной регрессионной модели состоит из следующих шагов:

Шаг 1. Результаты наблюдений разделяют на две части: обучающую (90-95% наблюдений) и контролирующую (оставшиеся наблюдения) выборки;

Шаг 2. По обучающей выборке выполняется оценка параметров модели 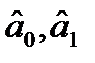методом наименьших квадратов и строится регрессионная модель ;

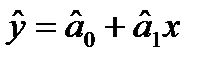Замечание. Предполагается, что выполняются все условия теоремы Гауса-Маркова.

Шаг 3. По построенной модели строится прогноз значений объясняющей переменной 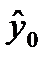из контролирующей выборки и доверительные интервалы для истинных значений;

Прогнозное значение 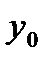определяется путем подстановки в уравнение регрессии 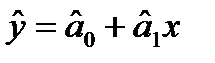соответствующего прогнозного значения 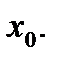Затем вычисляется средняя стандартная ошибка прогноза

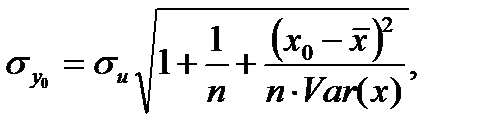где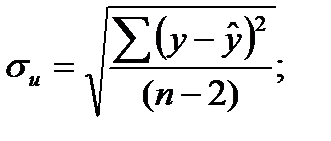

или используя другую формулу для парной регрессии

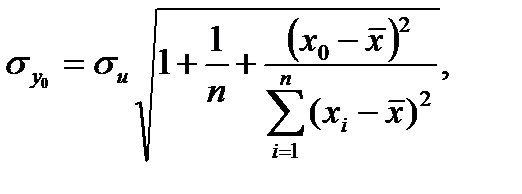(1.33)

где n – число элементов в учебной выборке.

После это строится доверительный интервал прогноза

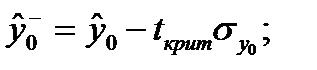(1.34)

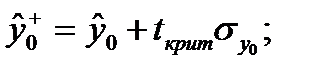
Интервал может быть достаточно широк за счет малого объема наблюдений.

Шаг 4. Проводится проверка: если выборочное значение 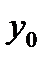из контролирующей выборки накрывается доверительным интервалом — модель признается адекватной, в противном случае — подлежит доработке

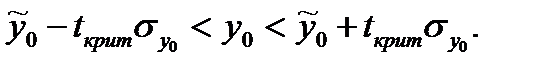(1.35)

См. дополнительно литературу: [1, с. 31 - 62]; [2, с. 317 -346]; [3, c. 72 -117]; [5, с. 64 - 70]; [7, с. 48 - 57]; [8]; [9].

Пример построения и исследования парной линейной эконометрической модели

Задача. Сотрудник муниципального образования должен подготовить обоснованные предложения к проекту плана развития района на 2014 и 2015 гг. по графе «Потребительские расходы в расчете на душу населения» в зависимости от средней заработной платы и выплат социального характера. У сотрудника имеются статистические данные по этим показателям с 1990 г. по 2013 г. (см. табл. 2.1). При этом планом предусмотрено, что в 2014 г рост заработной платы и выплаты социального характера увеличатся на 8% по сравнению со средним значением за последние 5 лет, а в 2015 г – увеличатся на 12%.

Таблица 2.1

№	Год	Потребительские расходы в расчете на душу населения, тыс. руб., у	Средняя заработная плата и выплаты социального характера, тыс. руб., х
		?	8,0%
		?	12,0%

В качестве исследования сначала выбираем вариант парной линейной эконометрической модели вида:

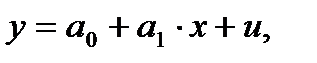
Что же предстоит сделать, чтобы ответить на поставленный в задаче вопрос?

1. Определить форму связи между переменными х и у.

2. Оценить параметры парной линейной регрессии, предполагая, что соблюдаются условия теоремы Гауса-Маркова.

3. Построить график исходной модели и на него «наложить» график полученной парной регрессии.

4. Построить график остатков полученной парной линейной регрессии и по нему определить их характер.

5. Проверить выполнение отдельных условий теоремы Гауса-Маркова: проверить остатки на гомоскедастичность и на автокорреляцию.

6. Оценить тесноту связи между переменными х и у, используя для этого показатели корреляции и детерминации.

7. Оценить силу связи объясняемой переменной с объясняющей с помощью среднего коэффициента эластичности.

8. Оценить с помощью средней ошибки аппроксимации качество полученной регрессии, т.е. отклонение расчетных значений от фактических.

9. Оценить статистическую надежность результатов по полученной регрессии с помощью F – критерия Фишера.

10. Оценить качество полученных параметров парной регрессии.

11. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученные параметры регрессии на адекватность.

12. Определить доверительный интервал прогноза для уровня значимости α = 0,5 и проверить полученную регрессию на адекватность.

13. Рассчитать прогнозные значения по графе «Потребительские расходы в расчете на душу населения» в зависимости от средней заработной платы и выплат социального характера на 2014 и 2015 годы.

14. Результаты проведенных исследований следует внести в отчет (см. Приложение 2).

Занятие 1.

1. Коэффициент корреляции r_xy=0.82

2. Форма зависимости между объясняемой y и объясняющей x переменными, если построить график y=f(x) (см. рис. 2.1.), будет нелинейной.

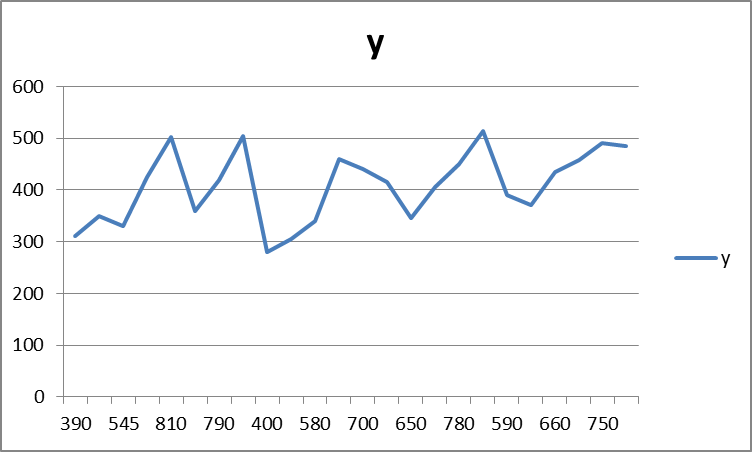
Рисунок 2.1.

3. Расчет параметров парной линейной регрессии.

Для расчета параметров парной линейной регрессии представленной эконометрической модели используем формулы (1.10) и (1.11):

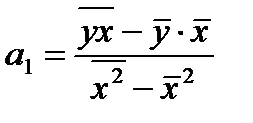
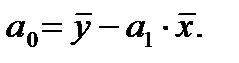
Для этого предварительно рассчитаем следующие значения:

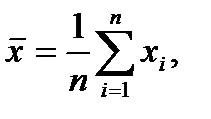
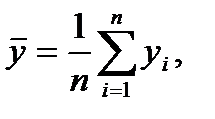
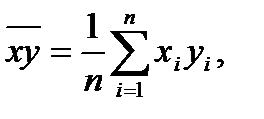
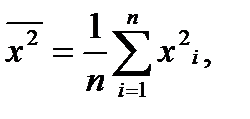
Расчет параметров а₀ и а₁ представлен в таблице 2.2.

В результате расчетов получаем

а₀ = 132,15; а₁ = 0,4186.

Таблица 2.2.

№	Год	y	x	xy	x2
Среднее значение	407,71	658,33	275792,7	451045,8

4. Построим график исходной модели и на него «наложим» график полученной парной линейной регрессии, см. рис. 2.2 (для этого предварительно надо рассчитать оценочные значения 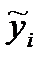, см. табл. 2.3.).

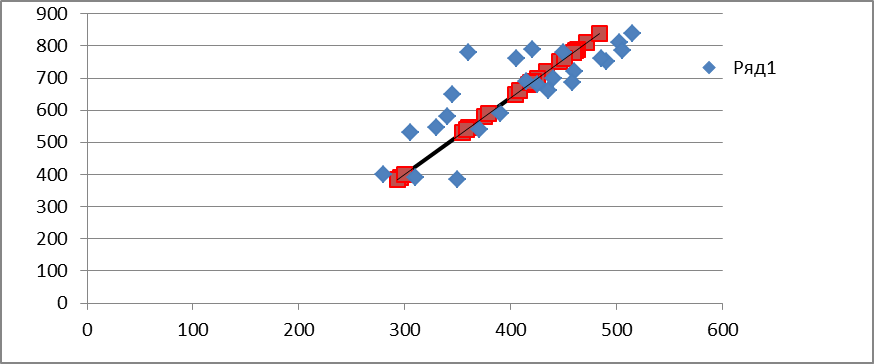
Рисунок 2.2

Таблица 2.3

x	y		E
		295,4	14,6
		293,3	56,7
		360,3	-30,3
		416,8	8,2
		471,2	30,8
		458,6	-98,6
		462,8	-42,8
		460,7	44,3
		299,6	-19,6
		354,0	-49,0
		374,9	-34,9
		433,5	26,5
		425,1	14,9
		421,0	-6,0
		404,2	-59,2
		450,3	-45,3
		458,6	-8,6
		483,7	31,3
		379,1	10,9
		358,2	11,8
		408,4	26,6
		418,9	39,1
		446,1	43,9
		450,3	34,7

5. Построим гистограмму остатков между исходными (статистическими) значениями переменой y и полученными 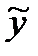в результате парной линейной регрессии (табл. 2.3, столбец e), см. рис. 2.3.

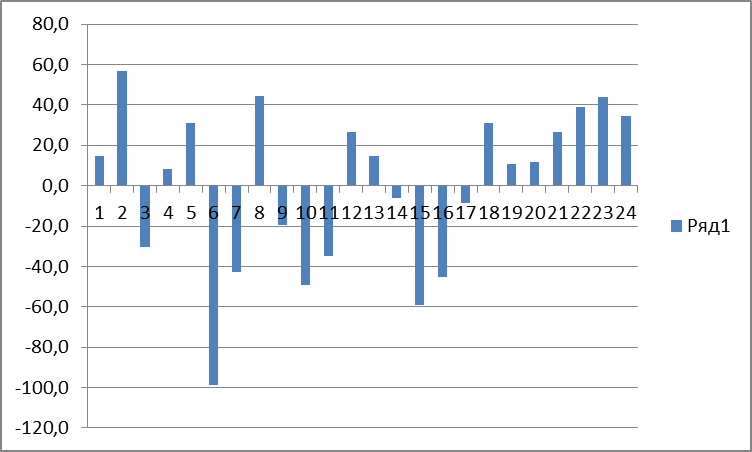
Рисунок 2.3.

По графику остатков можно судить, что они гомоскедастичные.

6. Проведем процедуру оценки параметров регрессионной парной линейной модели. Для этого воспользуемся инструментом Регрессия процедуры Анализ данных табличного процессора Excel, которая будет доступна, если подключить «Пакет анализа». При нажатии в основном меню табличного процессора Excel клавиши Данные становится возможной применение инструментов процедуры Анализ данных.

В высвечиваемом на экране окне Регрессия (см. рис. 2.4) надо внести значения y_i (Входной интервал Y) и значения х_i (Входной интервал Х). Можно также указать параметры вывода или оставить те, какие предлагает программа. После проведенных операций (назначений) нажать на клавишу ОК.

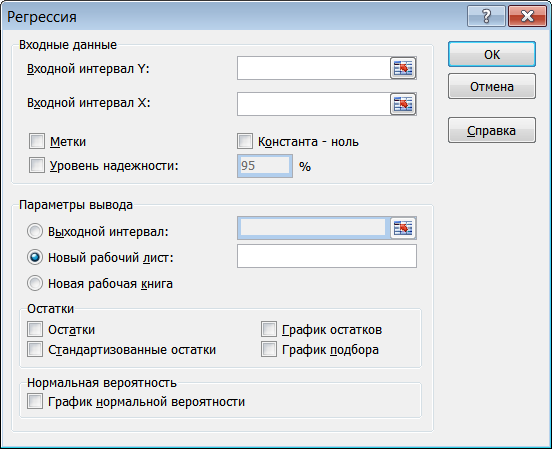
Рисунок 2.4

В результате выполнения инструмента Регрессия на экран дисплея выдается следующая информация, см. рис. 2.5 (результаты приведены для данных рассматриваемой задачи).

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,8202
R-квадрат	0,6728	R2
Нормированный R-квадрат	0,6579
Стандартная ошибка	40,4990	σ
Наблюде-ния
Дисперсионный анализ
	Df	SS	MS	F	Значимо-сть F
Регрессия		74183,235	74183,2359	45,229	9,27E-07
Остаток		36083,723	1640,169
Итого		110266,958
	Коэффициен-ты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересече-ние	132,155	41,799	3,162	0,0045	45,47	218,84
Переменная X1	0,419	0,062	6,725	9,27E-07	0,29	0,5476

Рисунок 2.5

Пояснения к рисунку 2.5[3]:

۰Множественный R – коэффициент корреляции Пирсона, равный корню квадратному из R-квадрат,

۰R-квадрат – коэффициент детерминации, характеризует тесноту связи объясняемой и объясняющих переменных,

۰Наблюдения – количество (n) наблюдений в массиве,

۰ df (Регрессия) – число объясняющих переменных,

۰df (Остаток) – число степеней свободы,

۰df (Итого) – Размер выборки минус 1,

۰SS (Регрессия) – RSS,

۰SS (Остаток) – ESS,

۰SS (Итого) – TSS,

۰F – статистика для оценки связи между объясняемой и объясняющими переменными,

۰Коэффициенты (Y-пересечение) – оценка параметра a₀,

۰Коэффициенты (Переменная X₁) - оценка параметра a₁,

۰Стандартная ошибка (Y-пересечение) – среднеквадратичная ошибка оцененного параметра a₀,

۰Стандартная ошибка (Переменная X₁) - среднеквадратичная ошибка оцененного параметра a₁,

۰t-Статистика (Y-пересечение) – отношение Коэффициент / Стандартная ошибка для параметра a₀,

۰t-Статистика (Переменная X₁) - отношение Коэффициент / Стандартная ошибка для параметра a₁,

۰P-Значение (Y-пересечение) – уровень значимости α для значений t-Статистика для параметра a₀,

۰P-Значение (Переменная X₁) – уровень значимости α для значений t-Статистика для параметра a₁,

۰Верхние и Нижние - границы доверительного интервала для параметров уравнения регрессии, вычисляемые при различных уровнях значимости α.

Сравните полученные значения параметров парной линейной регрессии с рассчитанными ранее по формулам (п.2) данного занятия.

Внимание!