Оценивание параметров парной линейной эконометрической модели

Для исходной парной линейной эконометрической модели, представленной в виде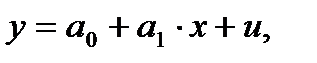необходимо построить парную линейную регрессию вида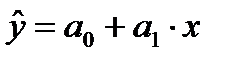

Построение линейной регрессии 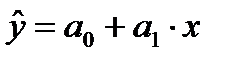сводится к оценке ее параметров 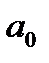и

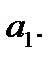
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 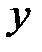от оценочного 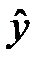минимальна, т.е.

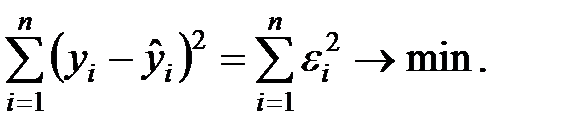(1.8)

Для линейной регрессии параметры 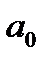и 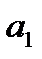находятся из системы нормальных уравнений:

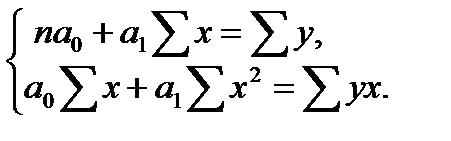(1.9)

Решая систему, находим оценку коэффициента парной линейной регрессии:

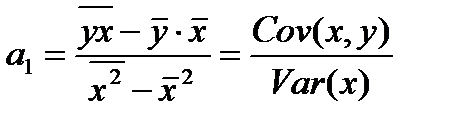(1.10)

и постоянный коэффициент

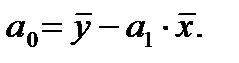(1.11)

Коэффициент 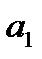при объясняющей переменной 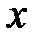показывает, насколько изменится в среднем величина 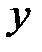при изменении значения 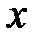на единицу.

См. дополнительно литературу: [1, с. 35 - 44]; [2, с. 148 - 153]; [3, с. 49 - 71]; [5, с. 50 - 56]; [7, с. 41 - 48]; [8]; [9].

Теорема Гауса-Маркова и проверка ее гипотез

Если имеется выборка значений переменных y и x

(y₁,x₁), (y₂, x₂), …. ,(y_n,x_n)

линейной модели парной регрессии 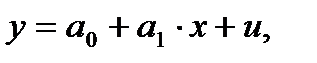то в рамках этой модели величины (y₁,x₁), (y₂, x₂), …. ,(y_n,x_n) связаны системой уравнений наблюдения объекта в виде линейных алгебраических уравнений:

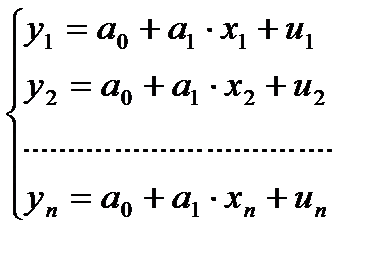(1.12)

Данная система называется схемой Гауса-Маркова. В матричном виде она имеет вид:

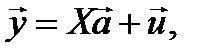(1.13)

где

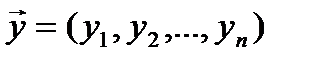- вектор наблюдений объясняющей переменной y,

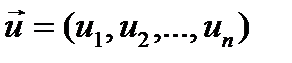- ненаблюдаемый вектор случайных возмущений (остатков),

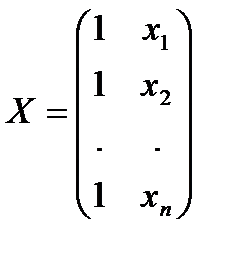- расширенная матрица наблюдаемых значений объясняющей переменной x,

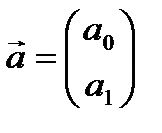- вектор столбец неизвестных параметров парной линейной эконометрической модели, которые подлежат оцениванию по имеющейся выборке.

Теорема Гауса-Маркова

Если имеется матрица X уравнений наблюдений размером n x (k+1), где n > k+1, имеющая линейно-независимые столбцы, а случайные возмущения u_i (i == 1,n), удовлетворяют следующим условиям:

E(u₁) = E(u₂) = … = E(u_n) = 0, (1.14)

Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u², (1.15)

Cov(u_i,u_j) = 0 для всех i ≠ j, (1.16)

Cov(x_i,u_j) = 0 для всех i и j, (1.17)

то тогда наилучшей линейной процедурой нахождения параметров эконометрической модели является метод наименьших квадратов (МНК), позволяющий найти эффективные и несмещенные оценки параметров модели.

При этом предполагается, что случайные остатки в уравнениях наблюдений распределены по нормальному закону.

Таким образом, для того, чтобы воспользоваться МНК для оценки параметров парной эконометрической модели, необходимо соблюдение всех четырех условий теоремы Гауса-Маркова.

Если соблюдается условие (1.15), то говорят, что случайные остатки в модели гомоскедастичные, в противном случае – гетероскедастичные.

См. дополнительно литературу: [1, с. 45 - 47]; [2, с. 153 - 162]; [3, с. 72 - 117]; [5, с. 60 - 64]; [7, с. 155 - 169]; [8]; [9].

Тест Голдфелда-Квандта

Тест Голдфелда-Квандта предназначен для проверки условия (1.15) теоремы Гауса-Маркова о гомоскедастичности случайного остатка в модели, т.е. проверяется статистическая гипотеза о равенстве дисперсий случайных остатков в наблюдаемых уравнениях

Н₀: Var(u₁) = Var(u₂)= …= Var(u_n) = σ_u²

Реализация теста осуществляется по следующему алгоритму:

Шаг 1. Уравнения наблюдений 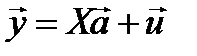упорядочивают по возрастанию объясняющей переменной x.

Шаг 2. Полученный отсортированный массив разбивают на две равные части (n₁ = n₂ = n/2). Если массив большой или количество значений в массиве нечетное (для небольших массивов), то его разбивают на 3 части (n₁ = n₃ ≈ 0,3n). При этом число элементов в первой части и число элементов в третьей части должны быть одинаковыми.

Шаг 3. Для первой части отсортированного массива рассчитывается величина ESS₁[1]:

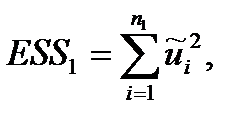(1.18)

где 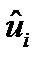- оценка случайного возмущения (остатков) u_i

Шаг 4. Аналогично рассчитывается величина ESS₂ для другой части отсортированного массива:

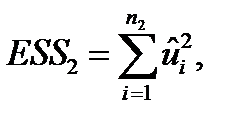
Шаг 5. Вычисляется статистика Голдфелда-Квандта (GQ):

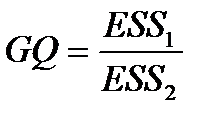и обратная ей 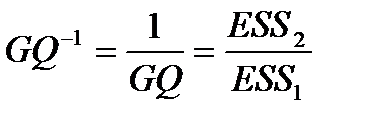(1.19)

Шаг 6. Задается уровень значимости α и при количествах степеней свободы обоих частей массива v₁ = v₂ = n₁-(k+1) определяется F_крит = F_1-α распределения Фишера по таблице 1 (см. Приложение 1), либо, если для расчетов применяется табличный процессор Excel, то F_крит можно рассчитать, используя функцию FРАСПОБР(1- α; v₁, v₂).

Шаг 7. Гипотеза Н₀ принимается, если справедливы следующие два неравенства

GQ ≤ F_крит ,

GQ^-1 ≤ F_крит , (1.20)

т.е. случайный остаток в парной эконометрической модели в этом случае полагается гомоскедастичным. В противном случае гипотеза Н₀ отклоняется и делается вывод, что случайный остаток в парной эконометрической модели является гетероскедастичным.

См. дополнительно литературу:[1, с. 32 - 49 ], [2, с. 186 - 189]; [5, с. 157 - 163]; [7, с. 41 - 48, с. 62 - 80]; [8]; [9].

Тест Дарбина – Уотсона

Тест Дарбина – Уотсона предназначен для проверки условия (1.3) теоремы Гауса - Маркова, т.е. проверки следующей гипотезы Н₀:

Н₀: Cov(u_i,u_j) = 0 для всех i ≠ j

Реализация теста осуществляется по следующему алгоритму:

Шаг 1. По уравнениям наблюдений 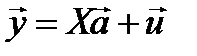вычисляются оценки параметров модели и оценки случайных остатков .

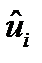Шаг 2. Вычисляется значение статистики Дарбина – Уотсона (DW) по формуле:

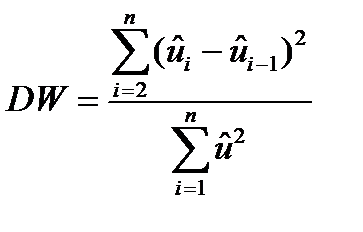(1.21)

Областью изменения статистики DW является интервал (0,4).

Шаг 3. Из таблицы 2 (см. Приложение 1) по количеству наблюдений (n) и количеству (k) объясняющих переменных выбираются значения величин d_L и d_U.

Шаг 4. Проводится проверка, в какой из пяти подмножеств (0, d_L), (d_L, d_U,), (d_U, 4- d_U), (4- d_U, 4- d_L), (4- d_L, 4) интервала (0,4)попадает рассчитанное значение статистики DW (см. рис. 1.1), и делается вывод:

	cov>0	?	cov=0	?	cov<0
	dL	dU		4-dU	4-dL

Рисунок 1.1.

а) если значение статистики DW попадает в третий интервал (d_U, 4- d_U), то подтверждается гипотеза:

Н₀: Cov(u_i,u_j) = 0 для всех i ≠ j,

б) если значение статистики DW попадает в первый интервал (0, d_L), то гипотеза Н₀ не подтверждается, а принимается альтернативная гипотеза:

Н₁: Cov(u_i,u_j) > 0,

в) если значение статистики DW попадает в пятый интервал (4- d_L, 4), то гипотеза Н₀ не подтверждается, а принимается альтернативная гипотеза:

Н₁: Cov(u_i,u_j) < 0,

г) если значение статистики DW попадает во второй (d_L, d_U,) или четвертый (4- d_U, 4- d_L) интервал, то отклонить или принять гипотезу Н₀ не удается с использованием данного теста.

Тест Дарбина-Уотсона предполагает, что соблюдаются другие условия теоремы Гауса-Маркова.

См. дополнительно литературу:[1, с .32-49], [2, с. 60 - 63, с. 331 - 332]; [3, с. 72-117]; [5, с. 170 - 178]; [7, с. 272 - 278]; [8]; [9].