Проектирование горизонтальной площадки. Подсчет объемов земляных работ.

Проектирование горизонтальной площадки обычно производится с соблюдением условия нулевого баланса земляных работ. Под этим условием понимается сведение земляных работ к минимуму и обеспечение равенства объемов выемки и подсыпки. Под вертикальной планировкой подразумевается преобразование естественного рельефа при строительстве в горизонтальную или наклонную площадки путем выполнения земляных работ по специальному проекту вертикальной планировки.

1. Для проектирования горизонтальной площадки вычисляют среднюю отметку всего участка по известным отметкам вершин квадратов по формуле:

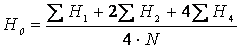; где N – число квадратов; H1, H2, H4 – отметки вершин квадратов, относящихся к одному, двум и четырем квадратам. Результаты заносят в таблицу. Среднюю отметку Н 0 вычисляют с точностью до 0,01 м. Рабочие отметки всех вершин квадратов получают как разности отметок поверхности земли в вершинах квадратов и отметки Н 0. h раб = Н n – H 0. Отрицательная рабочая отметка указывает на насыпь грунта в данной точке, а положительная – на выемку. Рабочие отметки подписываются красной тушью под отметками поверхности земли и с помощью их строят линию нулевых рабочих отметок, называемую линией нулевых работ. Точки нулевых рабочих отметок можно определить графоаналитическим или графическим способами. Графоаналитический способ заключается в вычислении расстояний х до точек нулевых рабочих отметок (нулевых работ), а затем в графическом определении на плане по х положения искомой точки на стороне квадрата или его диагонали. Расстояние до точек нулевых работ определяют по известной формуле:

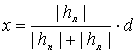; Для контроля 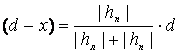, где d – сторона квадрата (здесь d = 10 м); h л ,h п – рабочие отметки вершин квадрата, расположенные слева и справа от точки нулевых работ. Величины х и d-x, вычисленные по формулам, должны составлять в сумме величину d. Графический способ состоит в определении положения точки нулевых работ путем графических построений. Получив таким образом ряд нулевых работ, соединяют их плавной пунктирной линией красного цвета, которая будет являться линией нулевых работ. Она разделяет площадку на участки выемки и насыпи. Участок насыпи показывают штриховкой. После вычисления рабочих отметок и построения линии нулевых работ подсчитывают объемы земляных работ. 2. Для проектирования наклонной площадки принимают уклон I = 0,05 c севера на юг. Проектную отметку начальной линии принимают равной Н 0. Эту линию располагают посередине площадки. Зная проектную отметку начальной линии Н 0 и заданный уклон I проектируемой наклонной площадки, вычисляют проектные отметки Н к вершин всех квадратов по формуле: H k = H 0 +( 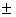I a), Где а – горизонтальное расстояние между начальной и определяемой точками. Учитывая направления уклона I, знак «+» относится к точкам, лежащим выше начальной. А знак «-« - к точкам, лежащим ниже ее. Затем вычисляют рабочие отметки вершин всех квадратов как разность между отметками поверхности земли H n в вершинах квадратов и вычисленными проектными отметками Н к: H раб = H n - Н к. Подсчет объемов земляных работ при вертикальной планировкеДля подсчета объемов земляных работ составляют картограмму земляных работ, на которую выписывают отметки поверхности земли, проектные и рабочие отметки всех вершин квадратов. Положительный знак hраб рабочей отметки указывает на необходимость выемки грунта в этой точке. А отрицательный знак – на подсыпку. Линия нулевых работ является границей между площадью насыпи и выемки. Подсчет объемов земляных работ можно произвести четырьмя способами:

1. Способ треугольных призм: Для получения треугольных призм во всех квадратах строят треугольники и объем насыпи V н (в) каждой треугольной призмы подсчитывают по формуле:

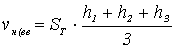, где SТ – площадь основания треугольной призмы, м2; h1,h2,h3 – рабочие отметки в углах основания призмы (или отметки вершин квадратов), м. Общий объем насыпи и выемки грунта по всей площадке получают суммированием соответствующих объемов каждой треугольной призмы.

2. Способ четырехугольных призм: каждая четырехугольная призма ограничена вертикальными плоскостями, плоским основанием и наклонной верхней плоскостью. Высоту призмы принимают равной среднему арифметическому hср из рабочих отметок h1, h2, h 3, h4 – угловых точек ее поверхности:

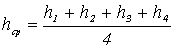. Тогда объем V в (н) выемки (или насыпи) грунта для каждого квадрата сетки подсчитывают, пользуясь формулой: V в (н) =S2 h ср, Где S2 –площадь основания четырехугольной призмы, м2. Общий объем насыпи и выемки грунта по всей площадке также получают суммированием соответствующих объемов всех четырехугольных призм.

3. Способ Стрельчевского: Подсчет объемов земляных работ производят по формулам:

,

.

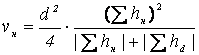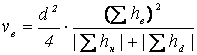Где vн, vв – объем насыпи и выемки грунта в каждом квадрате, м3; 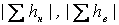- арифметическая сумма рабочих отметок насыпи и выемки грунта в квадрате, м; d – сторона квадрата, 10 м. Подсчет объемов земляных работ сводят в таблицу. Расхождение объемов выемки и насыпи грунта по всей площадке не должно превышать 5%.

41. Проектирование горизонтальной площадки. Подсчет объемов земляных работ.

Проектирование горизонтальной площадки обычно производится с соблюдением условия нулевого баланса земляных работ. Под этим условием понимается сведение земляных работ к минимуму и обеспечение равенства объемов выемки и подсыпки. Под вертикальной планировкой подразумевается преобразование естественного рельефа при строительстве в горизонтальную или наклонную площадки путем выполнения земляных работ по специальному проекту вертикальной планировки.

1. Для проектирования горизонтальной площадки вычисляют среднюю отметку всего участка по известным отметкам вершин квадратов по формуле:

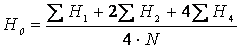; где N – число квадратов; H1, H2, H4 – отметки вершин квадратов, относящихся к одному, двум и четырем квадратам. Результаты заносят в таблицу. Среднюю отметку Н 0 вычисляют с точностью до 0,01 м. Рабочие отметки всех вершин квадратов получают как разности отметок поверхности земли в вершинах квадратов и отметки Н 0. h раб = Н n – H 0.

Отрицательная рабочая отметка указывает на насыпь грунта в данной точке, а положительная – на выемку. Рабочие отметки подписываются красной тушью под отметками поверхности земли и с помощью их строят линию нулевых рабочих отметок, называемую линией нулевых работ. Точки нулевых рабочих отметок можно определить графоаналитическим или графическим способами. Графоаналитический способ заключается в вычислении расстояний х до точек нулевых рабочих отметок (нулевых работ), а затем в графическом определении на плане по х положения искомой точки на стороне квадрата или его диагонали. Расстояние до точек нулевых работ определяют по известной формуле:

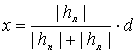; Для контроля 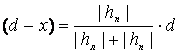, где d – сторона квадрата (здесь d = 10 м); h л ,h п – рабочие отметки вершин квадрата, расположенные слева и справа от точки нулевых работ. Величины х и d-x, вычисленные по формулам, должны составлять в сумме величину d. Графический способ состоит в определении положения точки нулевых работ путем графических построений. Получив таким образом ряд нулевых работ, соединяют их плавной пунктирной линией красного цвета, которая будет являться линией нулевых работ. Она разделяет площадку на участки выемки и насыпи. Участок насыпи показывают штриховкой. После вычисления рабочих отметок и построения линии нулевых работ подсчитывают объемы земляных работ.

2. Для проектирования наклонной площадки принимают уклон I = 0,05 c севера на юг. Проектную отметку начальной линии принимают равной Н 0. Эту линию располагают посередине площадки. Зная проектную отметку начальной линии Н 0 и заданный уклон I проектируемой наклонной площадки, вычисляют проектные отметки Н к вершин всех квадратов по формуле: H k = H 0 +( 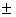I a), Где а – горизонтальное расстояние между начальной и определяемой точками.

Учитывая направления уклона I, знак «+» относится к точкам, лежащим выше начальной. А знак «-« - к точкам, лежащим ниже ее. Затем вычисляют рабочие отметки вершин всех квадратов как разность между отметками поверхности земли H n в вершинах квадратов и вычисленными проектными отметками Н к: H раб = H n - Н к.

Подсчет объемов земляных работ при вертикальной планировке

Для подсчета объемов земляных работ составляют картограмму земляных работ, на которую выписывают отметки поверхности земли, проектные и рабочие отметки всех вершин квадратов. Положительный знак hраб рабочей отметки указывает на необходимость выемки грунта в этой точке. А отрицательный знак – на подсыпку. Линия нулевых работ является границей между площадью насыпи и выемки.

Подсчет объемов земляных работ можно произвести четырьмя способами:

1. Способ треугольных призм: Для получения треугольных призм во всех квадратах строят треугольники и объем насыпи V н (в) каждой треугольной призмы подсчитывают по формуле:

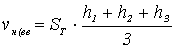, где SТ – площадь основания треугольной призмы, м2; h1,h2,h3 – рабочие отметки в углах основания призмы (или отметки вершин квадратов), м. Общий объем насыпи и выемки грунта по всей площадке получают суммированием соответствующих объемов каждой треугольной призмы.

2. Способ четырехугольных призм: каждая четырехугольная призма ограничена вертикальными плоскостями, плоским основанием и наклонной верхней плоскостью. Высоту призмы принимают равной среднему арифметическому hср из рабочих отметок h1, h2, h 3, h4 – угловых точек ее поверхности:

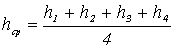. Тогда объем V в (н) выемки (или насыпи) грунта для каждого квадрата сетки подсчитывают, пользуясь формулой: V в (н) =S2 h ср, Где S2 –площадь основания четырехугольной призмы, м2. Общий объем насыпи и выемки грунта по всей площадке также получают суммированием соответствующих объемов всех четырехугольных призм.

3. Способ Стрельчевского: Подсчет объемов земляных работ производят по формулам:

,

.

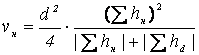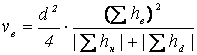Где vн, vв – объем насыпи и выемки грунта в каждом квадрате, м3; 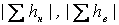- арифметическая сумма рабочих отметок насыпи и выемки грунта в квадрате, м; d – сторона квадрата, 10 м. Подсчет объемов земляных работ сводят в таблицу. Расхождение объемов выемки и насыпи грунта по всей площадке не должно превышать 5%.

Содержание и порядок производства тахеометрической съемки.

«Тахеометрия»(греч.)- «быстрое измерение». Цель ее – получение топографического плана местности (ситуация + рельеф). Основой ее являются теодолитно-нивелирные ходы: координаты вершин получают как в обычном теодолитном ходе, а отметки Н определяют путем геометрического нивелирования. Содержит полевые и камеральные работы.

Отличительные особенности съемки:

1) Съемка контуров и рельефа с пунктов съемочного обоснования выполняется полярным способом. При этом горизонтальные углы измеряют при одном (основном) положении вертикального круга, а расстояния по нитяному дальномеру.

2) Превышения и высоты съемочных точек определяют методом тригонометрического нивелирования, то есть измеряют угол наклона и расстояние до точки.

Полевые работы

1.Рекогносцировка: закрепление точек съемочного обоснования.

2.Прокладка теодолитно-нивелирного хода: те же работы, что и выше.

3.Съемка ситуации и рельефа:

а) Приведение теодолита (тахеометра) в рабочее положение: центрирование и горизонтирование.

б) Определение МО, измерение высоты инструмента i.

в) Ориентирование 0° лимба горизонтального круга вдоль одной из сторон хода, откладывание i на рейке.

г) съемка: измерение горизонтальных углов β, углов наклона ν, расстояний читанных по рейке (от теодолита до точки) D с занесением на абрис съемки.

Камеральные работы

1.Контроль полевых документов.

2.Вычисление Х, У, Н точек съемочного обоснования.

3.Обработка журнала тахеометрической съемки: вычисление ν, d, h, Η по тахеометрическим таблицам или по формулам.

V + h = h_{из табл.} + i; h = h_{из табл.}+ i – V; h_{из табл} = d·tgν; h = d·tgν + i – V, где i – высота инструмента, V – высота наведения, h – превышение, h_{из табл} – табличное превышение. Н = Н_ст.+h, Н_ст. – отметка станции, точки стояния теодолита, Н – отметка реечной точки.

5. Нанесение съемочных точек с помощью транспортира и линейки или тахеографа (совмещает в себе оба инструмента) способом полярных координат.

6. Вычерчивание ситуации и рельефа.

7. Оформление плана в соответствии с условными знаками.

(см.рисунок 97)

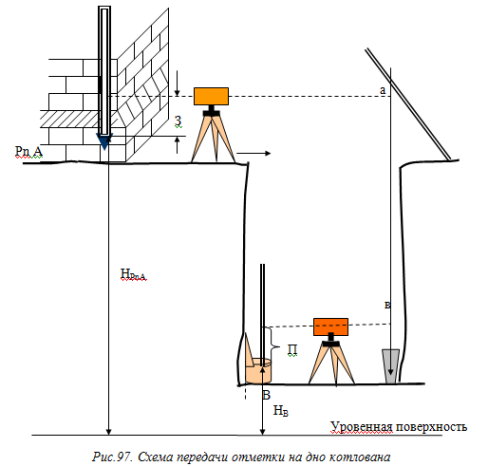
43. Сущность тригонометрического нивелирования. Нивелирование – это такой вид геодезических работ, при котором определяют абсолютные или условные высоты точек, или превышения между точками.Тригонометрическое (при помощи наклонного луча визирования,при этом измер угол наклона и расст между 2 т)).Тригонометрическое нивелирование называют также геодезическим или нивелированием наклонным лучом. Оно выполняется теодолитом; для определения превышения между двумя точками нужно измерить угол наклона и расстояние. В точке А устанавливают теодолит, в точке В - рейку или веху известной высоты V. Измеряют угол наклона зрительной трубы теодолита при наведении ее на верх вехи или рейки. Ошибка измерения превышения из тригонометрического нивелирования оценивается величиной от 2 см до 10 см на 100 м расстояния. При последовательном измерении превышений получается высотный ход; в высотном ходе углы наклона измеряют дважды: в прямом и обратном направлениях.

44. Содержание и порядок производства аэрофотосъемки. Для корректного прокладывания маршрута при аэрофотосъемке часть участка местности, сфотографированного на одном снимке, обязательно должна быть отображена и на другом. Эту особенность аэрофотоснимков называют продольным перекрытием. Продольное перекрытие — это отношение площади, сфотографированной на двух соседних снимках, к площади, изображённой на каждом отдельном снимке, выраженное в процентах. Обычно значение продольного перекрытия на аэрофотоснимках составляет 60 %, хотя в особенных случаях данные значения могут быть изменены в соответствии с требованиями к этим снимкам.Если требуется провести аэрофотосъёмку обширного по ширине участка, то фотографирование заданной площади производят серией параллельных маршрутов, имеющих поперечное перекрытие. При такой фотосъёмке стандартное значение перекрытия обычно составляет 30 %.Для проведения аэрофотосъёмки задаются высота полёта относительно фотографируемой местности, фокусное расстояние камеры аэрофотоаппарата, сезон, время и порядок прокладывания маршрутов.Из-за подвижности основания при аэрофотосъемке в каждый момент фотографирования центр проектирования объектива и плоскость аэроснимка занимают произвольное положение. Величины, определяющие пространственное положение снимка относительно принятой системы координат, называются элементами внешнего ориентирования снимка. Это три линейные координаты центра проектирования xs, ys, zs и три угла, определяющие поворот снимка вокруг трёх осей координат.

45.Порядок определения масштаба, продольного перекрытия снимков, базиса воздушного фотографирования. Дешифрировние аэрофотоснимков, составление фотоплана.Базисом воздушного фотографирования называется расстояние, пролетаемое самолетом между двумя экспозициями аэрофотоаппарата (расстояние, пролетаемое между двумя фотографированиями). Его можно вычислить по следующей формуле: В=N·в, где N – знаменатель масштаба снимка, в – расстояние в мм между главными точками двух снимков. Самолет выполняет параллельные залеты. При этом пара соседних снимков имеет продольное и поперечное перекрытие. Продольное перекрытие снимков – общая часть фотографируемой местности на предыдущем и последующем снимках (см. рис. 82). Вычисляют продольное перекрытие по следующей формуле: Р= 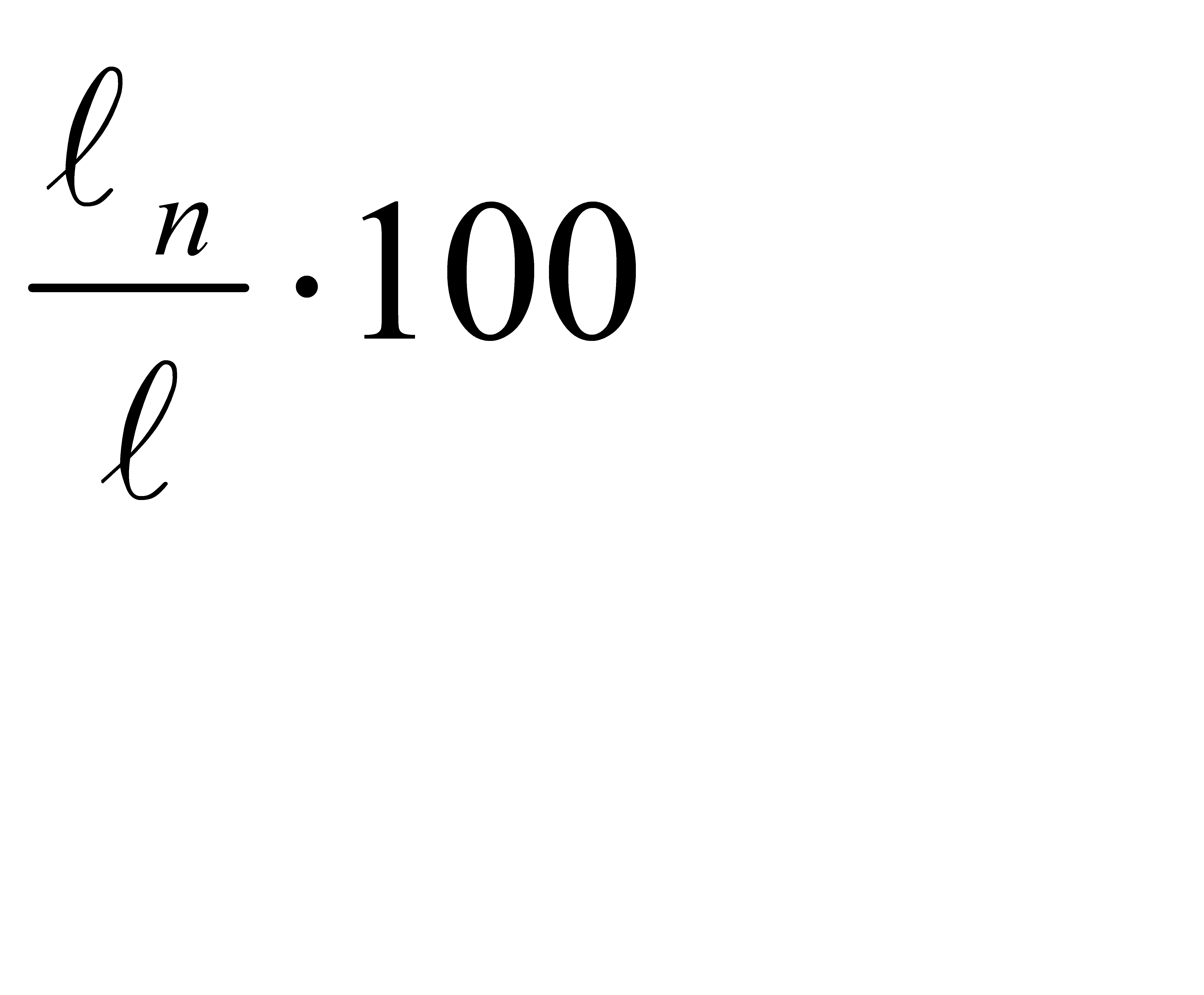%.., где ℓ_п – общая перекрывающаяся часть снимков, ℓ - длина стороны снимка.Величина его не должна быть менее 60% - в этом случае снимки образуют стереопару, по которой в дальнейшем получают план или карту местности. Ввиду того, что для стереофототопографического способа обработки снимков необходимы два соседних снимка с общей снятой площадью, то в процессе аэросъемки во время движения самолета по прямому направлению (по маршруту) фотографирование местности происходит через определенные интервалы (интервалометр), обеспечивающие перекрытие снимков не менее 60% в направлении (вдоль) маршрута (рис. 82). Это перекрытие называется продольным. Если съемка не маршрутная, а площадная, то предусматривается перекрытие соседних маршрутов не менее 30%, которое называется поперечным.Полевые работы кроме летно-съемочных работ включают также дешифрирование и привязку отпечатанных снимков.Дешифрирование снимков имеет целью расшифровать ситуацию, то есть распознать изображенные на снимках предметы и контуры местности, и может быть камеральным и полевым. Камеральное дешифрирование выполняют при помощи специальных приборов: стереоскопов и стереокомпараторов, которые позволяют получить стереоскопическое (объемное) изображение снятой местности. В результате обработки аэроснимков универсальным методом непосредственно получают графический план местности с контурами и рельефом.При дифференциальном методе процесс создания плана делится на два основных этапа.Первый этап – определение превышений точек аэроснимков или изображение на них рельефа горизонталями. Второй этап – получение контурной части карты в виде фотоплана или графического плана.

46.Классификация и свойства ошибок геодезических измеренийОпределением величины ошибок и их свойств занимается специальная дисциплина «Теория ошибок геодезических измерений».В практике различают 3 вида ошибок:а)грубые – пол-ся в рез-те грубых просчетов и неисправности приборов (просчет количества лент в длине линии, ошибка в отсчете десятков градусов на лимбе или числа дециметров на рейке). Они могут быть обнаружены и исключены путем повторного измерения величины.б)систематические – проявляются регулярно, обязательно в каждом измерении и обязательно одинаковы по модулю и знаку, действуют по одному принципу. Они вызваны в основном плохой юстировкой или неисправностью инструментов и приборов (20-ти метровая лента короче на 1см, коллимационная ошибка в теодолите). Исключаются из результатов измерений введением поправок и специальной методикой измерений (углы β при КП и КЛ, при нивелировании плечи делают равными, в длины линий вводят поправки за компарирование).в)случайные – являются следствием несовершенства органов чувств человека и недостаточной точности применяемых инструментов и приборов. Они не могут быть исключены из результатов измерений, но их влияние может быть ослаблено на основе изучения их свойств.

Если Х – истинное значение измеряемой величины, ℓ - измеренное значение, то случайная ошибка ∆ выражается формулой ∆=ℓ-Х.

Если одна и та же величина измерена несколько раз, то и количество ошибок будет большим. Получается ряд ошибок. Если измерения производятся приборами одинаковой точности, наблюдателями одинаковой квалификации, в одинаковых окружающих условиях, то они называются равноточными. Иначе-неравноточными.

В основу изучения случайных ошибок положено 4 их свойства, выведенных из изучения рядов ошибок равноточных измерений.1) При данных условиях измерений случайные ошибки не могут превосходить по абсолютной величине известного предела (свойство ограниченности).2) Одинаковые по абсолютной величине положительные и отрицательные случайные ошибки равно возможны, одинаково часто встречаются в ряду измерений.3) Чем больше абсолютная величина случайной ошибки, тем реже такая ошибка встречается в ряду измерений.4) Среднее арифметическое из случайных ошибок равноточных измерений одной и той же величины имеет тенденцию стремиться к 0 при неограниченном возрастании числа измерений (свойство компенсации). Математически это записывается так

Если соблюдены все четыре свойства в ряде ошибок, то говорят о «нормальном распределении».5) Если∆₁ ∆_n - 1-й ряд измерений; ∆₁' ∆_n' – 2-ой ряд измерений,

то 4-ое свойство распространяется и на сумму попарных произведений, то есть n→ ∞

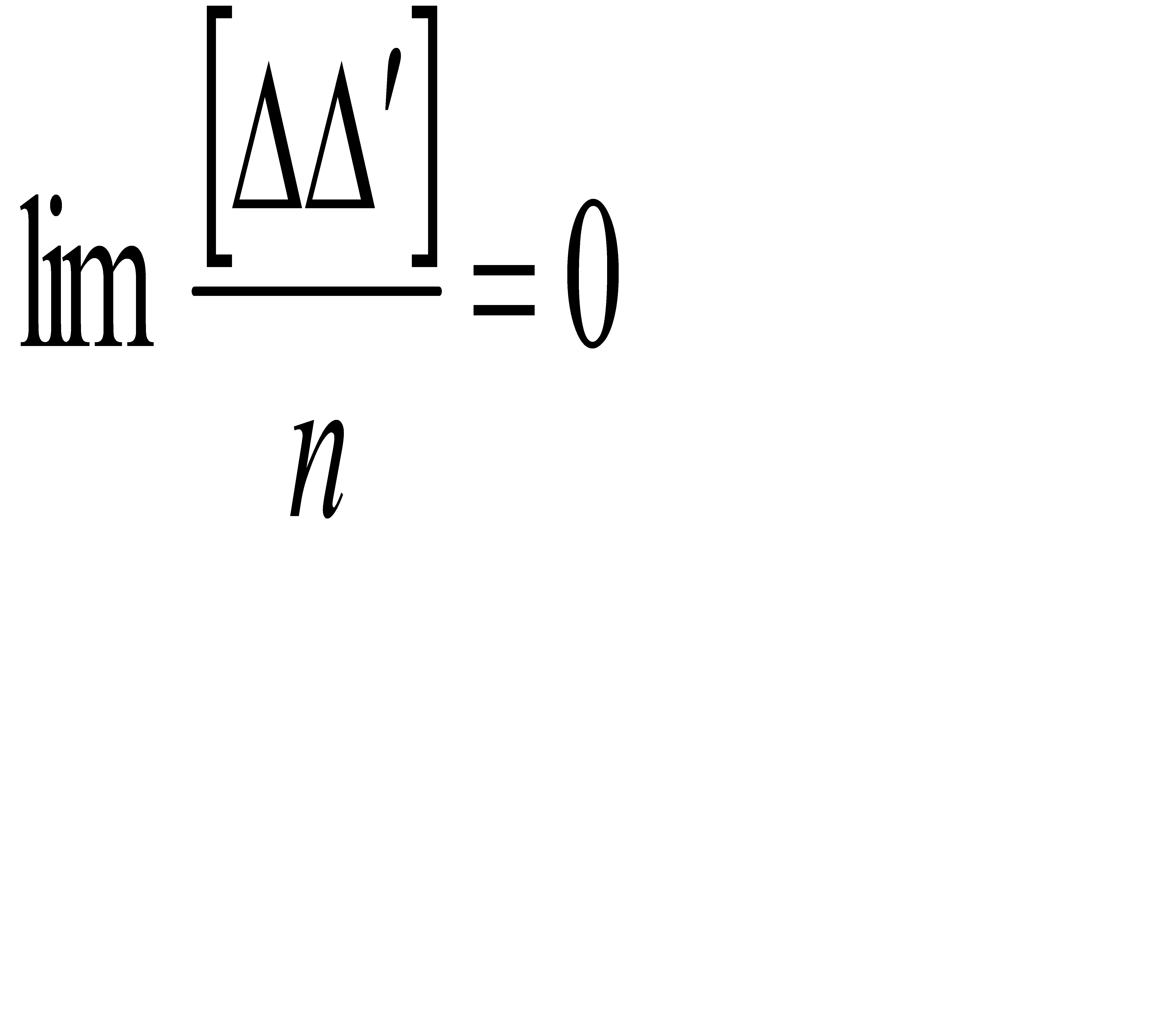
47.Средняя квадратическая, предельная и относительная ошибкиДля суждения о степени точности ряда измерений нужно иметь среднее значение ошибки. Среднее арифметическое из измерений нельзя брать, так как из-за разных знаков ряд с отдельными крупными ошибками может оказаться точнее ряда с меньшими ошибками: 25,5; 24,5; 25,0 – m_ср.=0 Х=25м

25,04; 24,97; 25,04 – m_ср.=0,02 м

Если взять ошибки по абсолютной величине, то два ряда измерений с одинаковыми по абсолютной величине средними ошибками могут быть ошибочно приняты равноточными и наличие крупных ошибок не будет отражено:

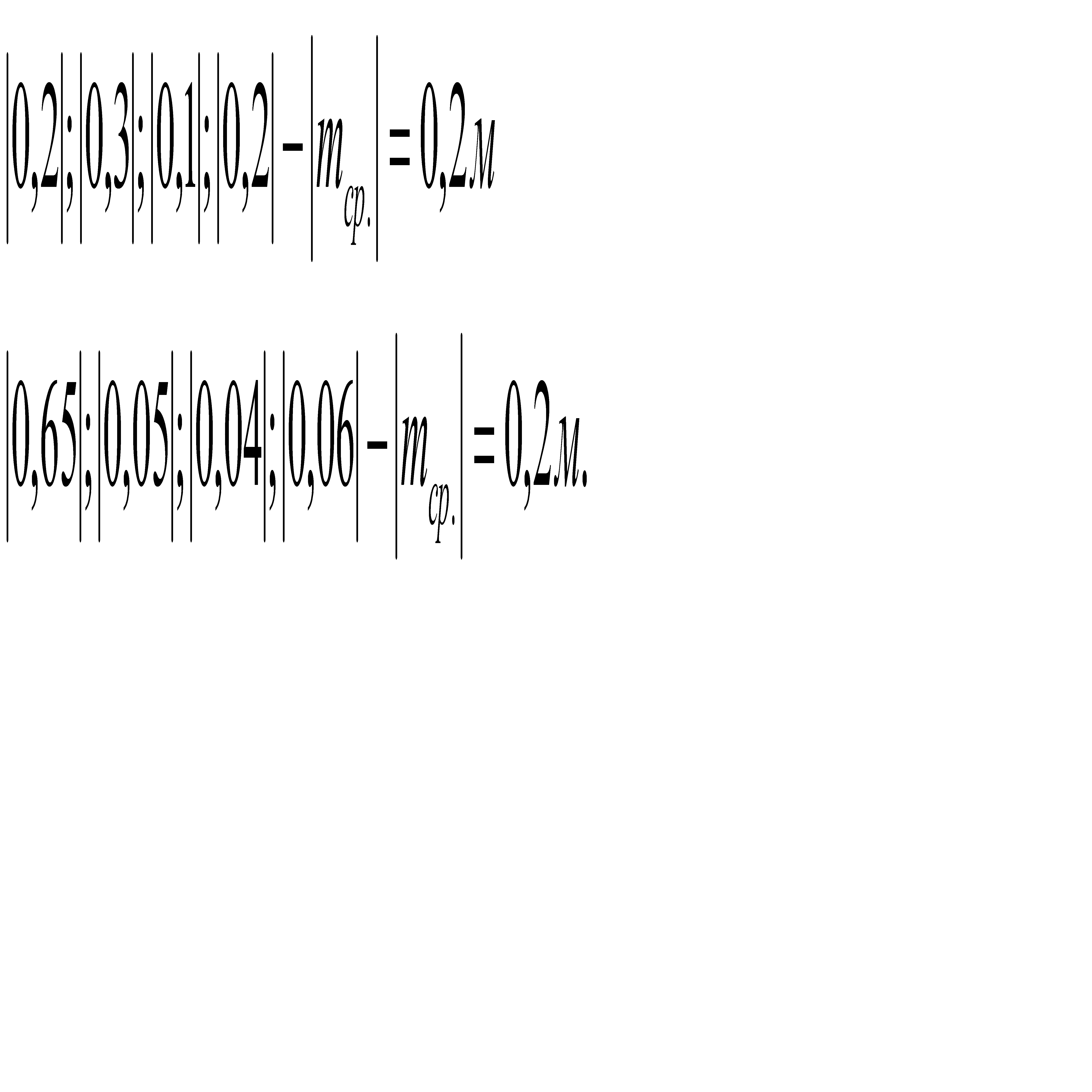
Поэтому в качестве критерия для оценки точности ряда измерений используют не зависящую от знаков отдельных ошибок и рельефно показывающую наличие крупных ошибок среднюю квадратическую ошибку. Квадрат этой ошибки принимают равным среднему арифметическому из квадратов отдельных случайных ошибок, то есть

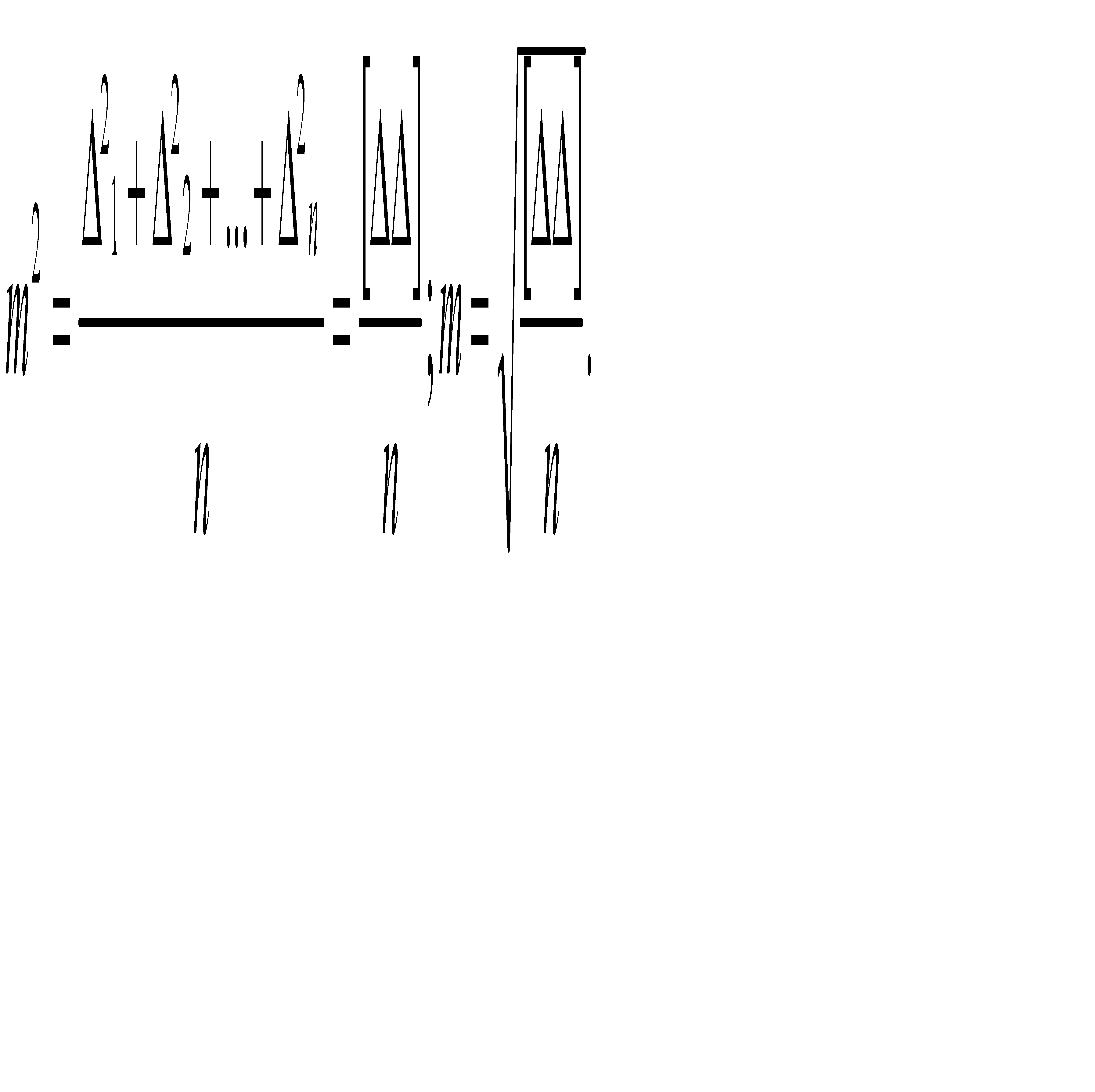
- формула Гаусса

По теории вероятностей подсчитано, что при большом количестве измерений случайная ошибка одного измерения превосходит m

∆>1m – в 32 случаях из 100 измерений

∆>2m – в 5 случаях из 100 измерений

∆>3m – в 3 случаях из 1000 измерений.

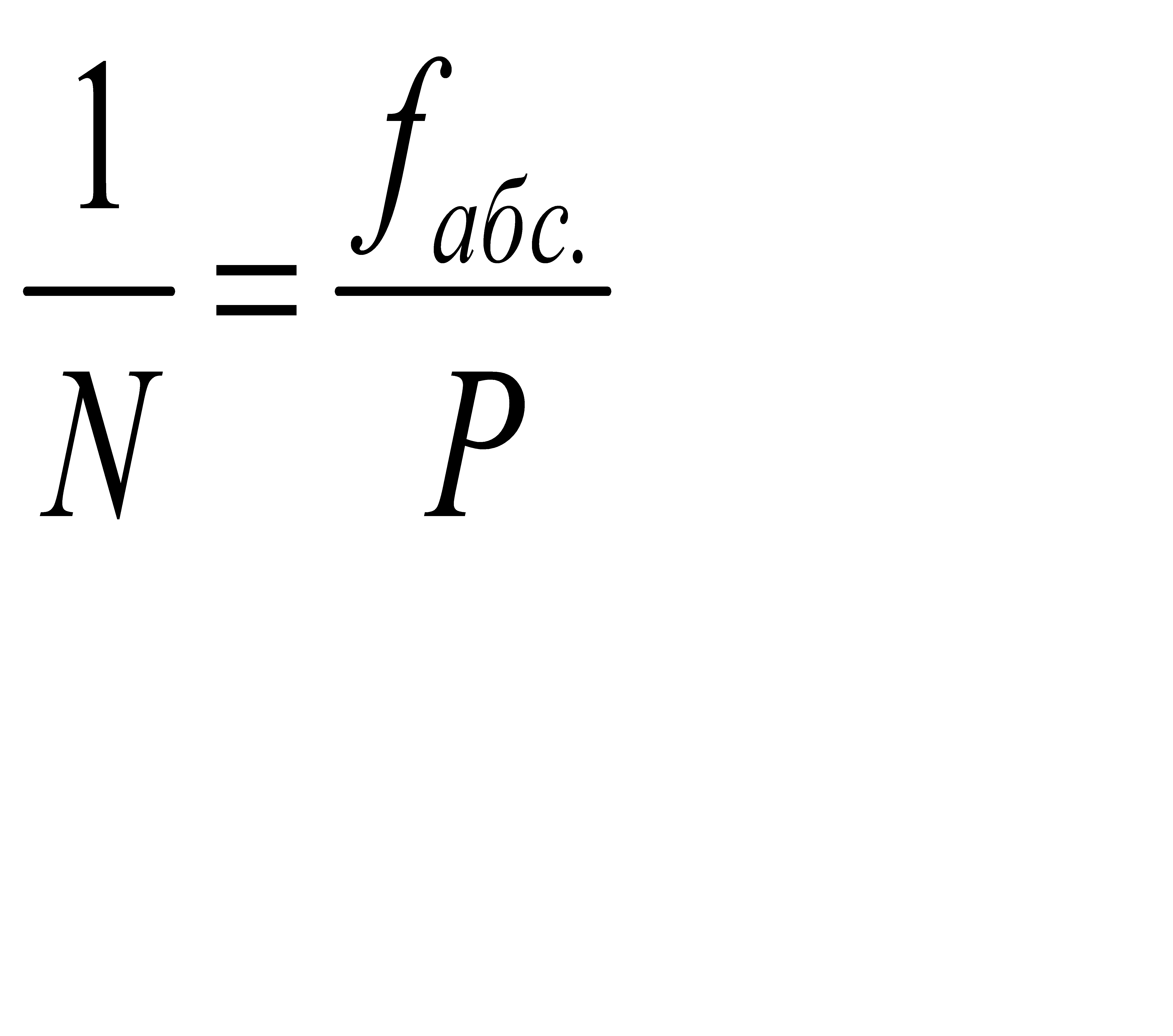
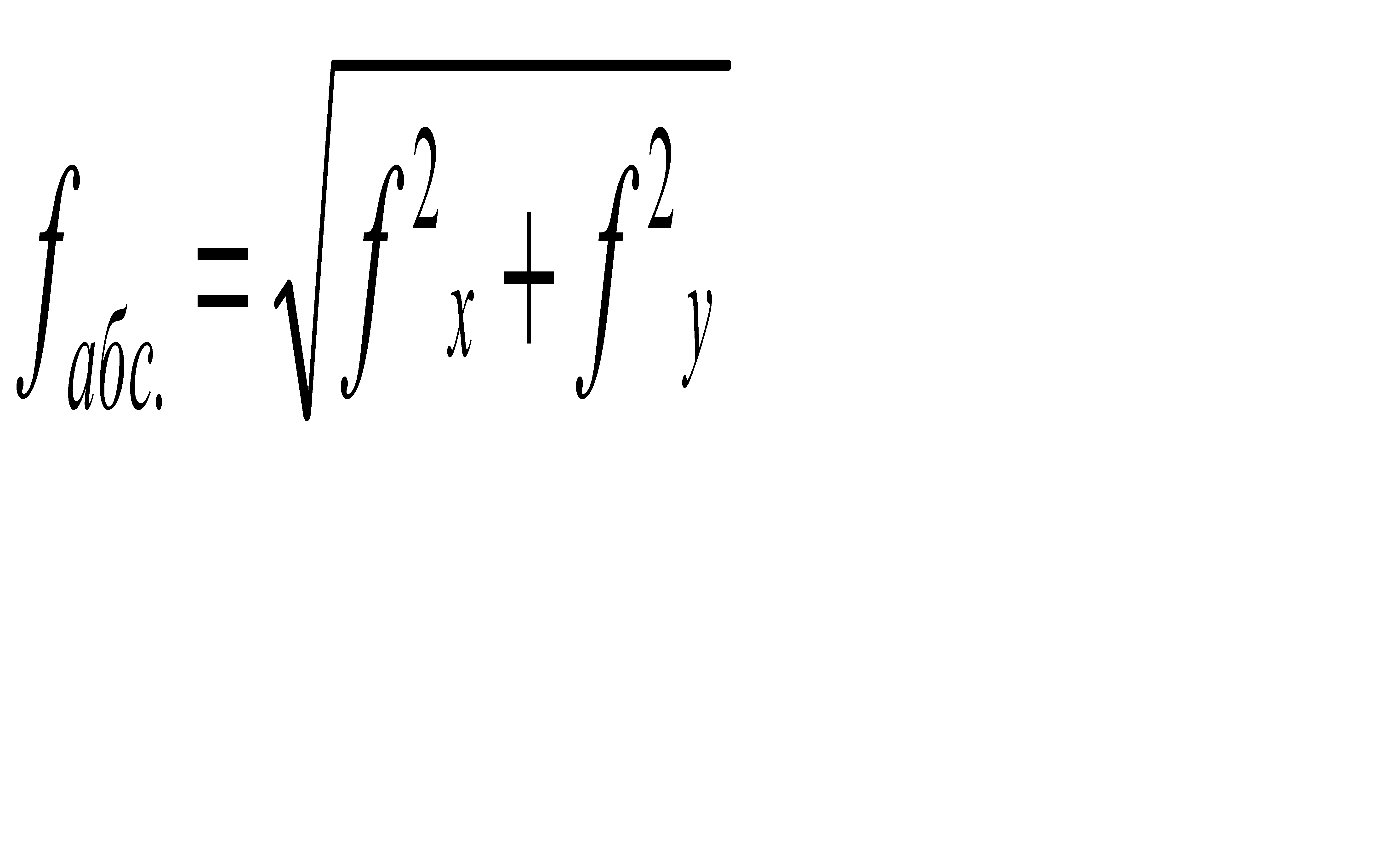
Поэтому утроенную среднюю квадратическую ошибку считают предельной∆_lim=3m.

Часто точность произведенных измерений лучше оценивается относительной ошибкой, то есть отношением абсолютной ошибки к измеряемой величине, выражаемой правильной дробью с числителем, равным 1. Эта ошибка характеризует в основном линейные измерения и измерения площади участков. Например, в замкнутом полигоне теодолитного хода линейные измерения оцениваются относительной ошибкой ; где - абсолютная ошибка, Р – периметр полигона.

48. Средняя квадратическая ошибка алгебраической суммы измеренных величин Функция вида z=x+y (суммы ); m_z=?

Дано: х – измерено несколько раз с ошибками ∆х₁; ∆х₂,… ∆х_{n; ;} у – измерено несколько раз с ошибками ∆у₁, ∆у₂,… ∆у_{n ;}z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,… ∆z_n. ; 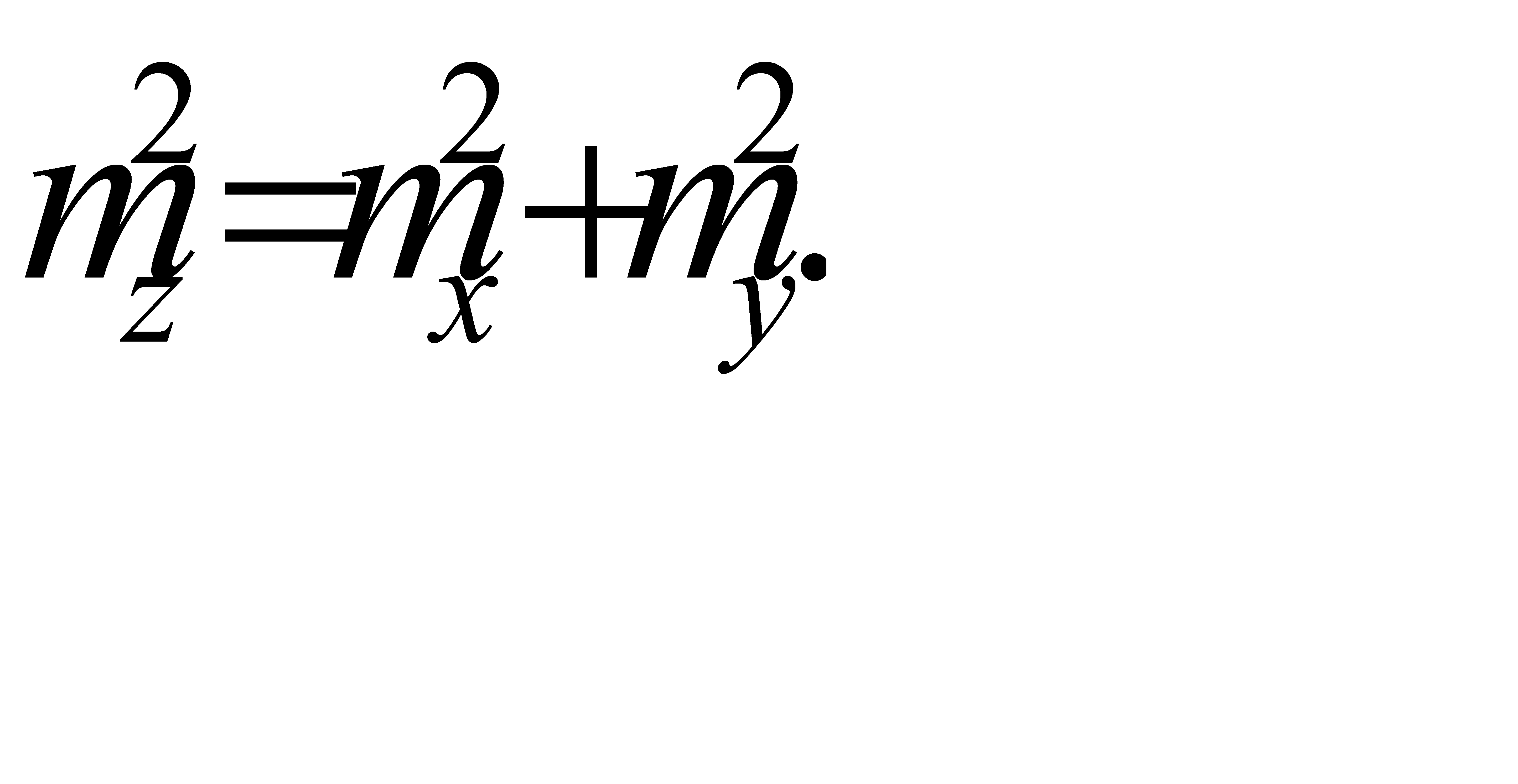Эта же формула справедлива для функции вида z=x-y, так как после выше приведенных рассуждений перед последним членом будет знак (-). Но он все равно стремится к нулю.Поэтому можно сделать вывод, что квадрат средней квадратической ошибки алгебраической суммы двух аргументов равен сумме квадратов средних квадратических ошибок слагаемых.Если m_х=m_у=m, то m_z=± 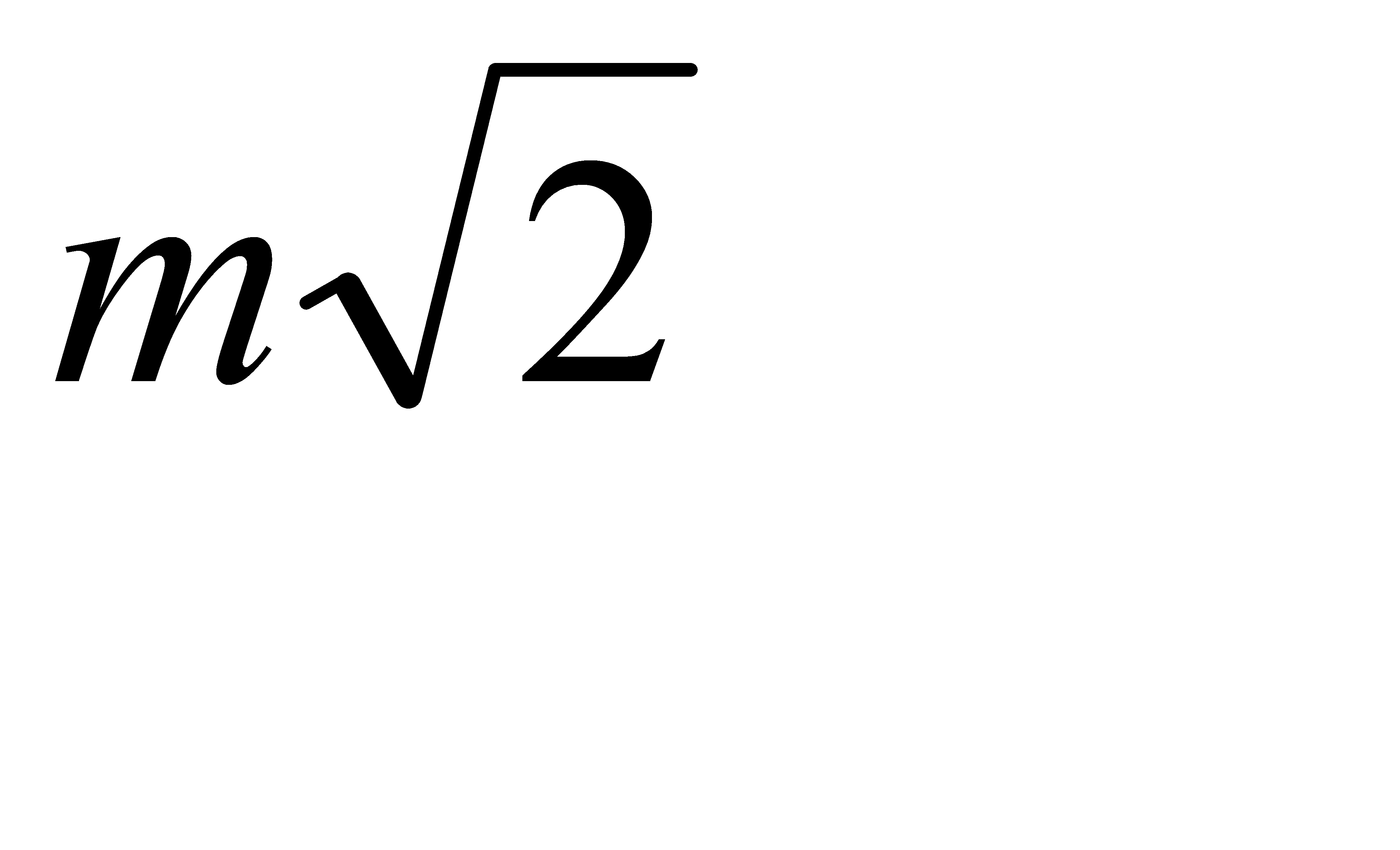.Пусть 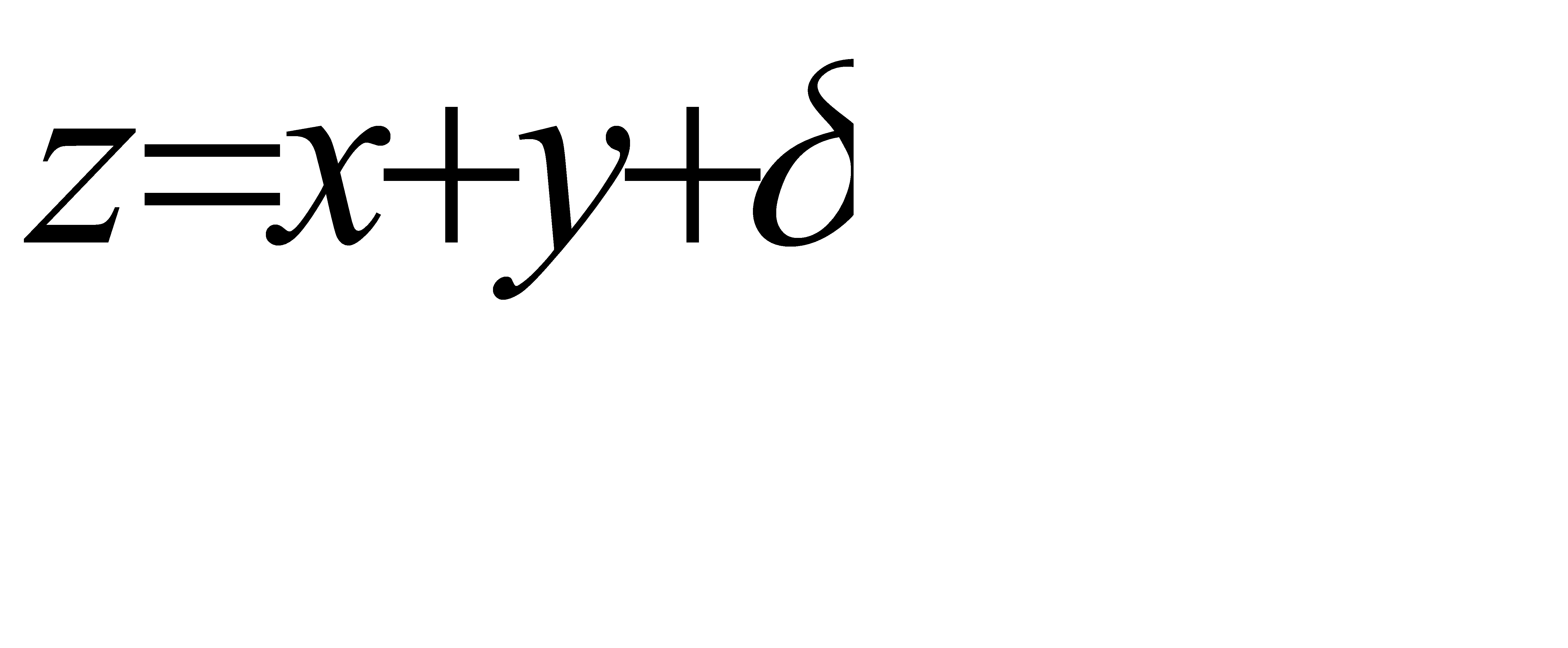, перепишем 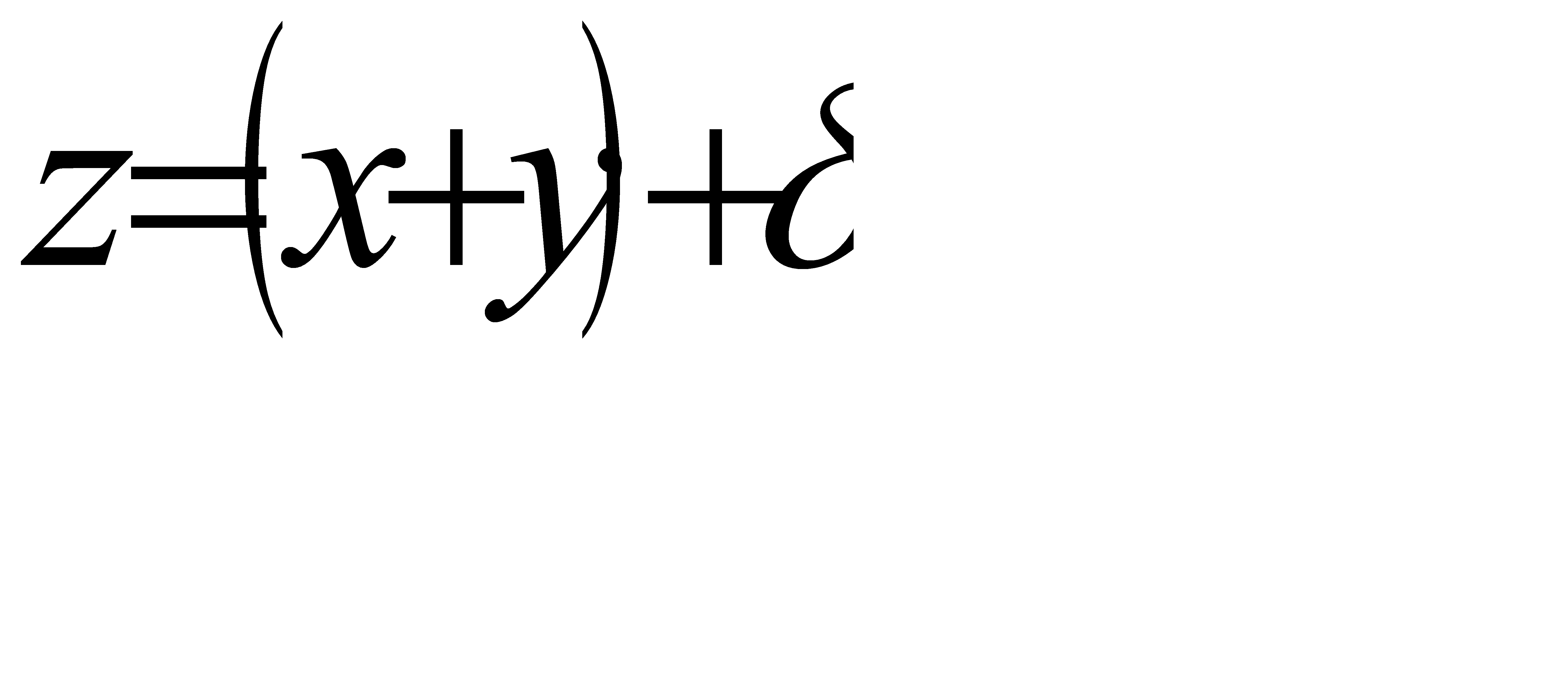. 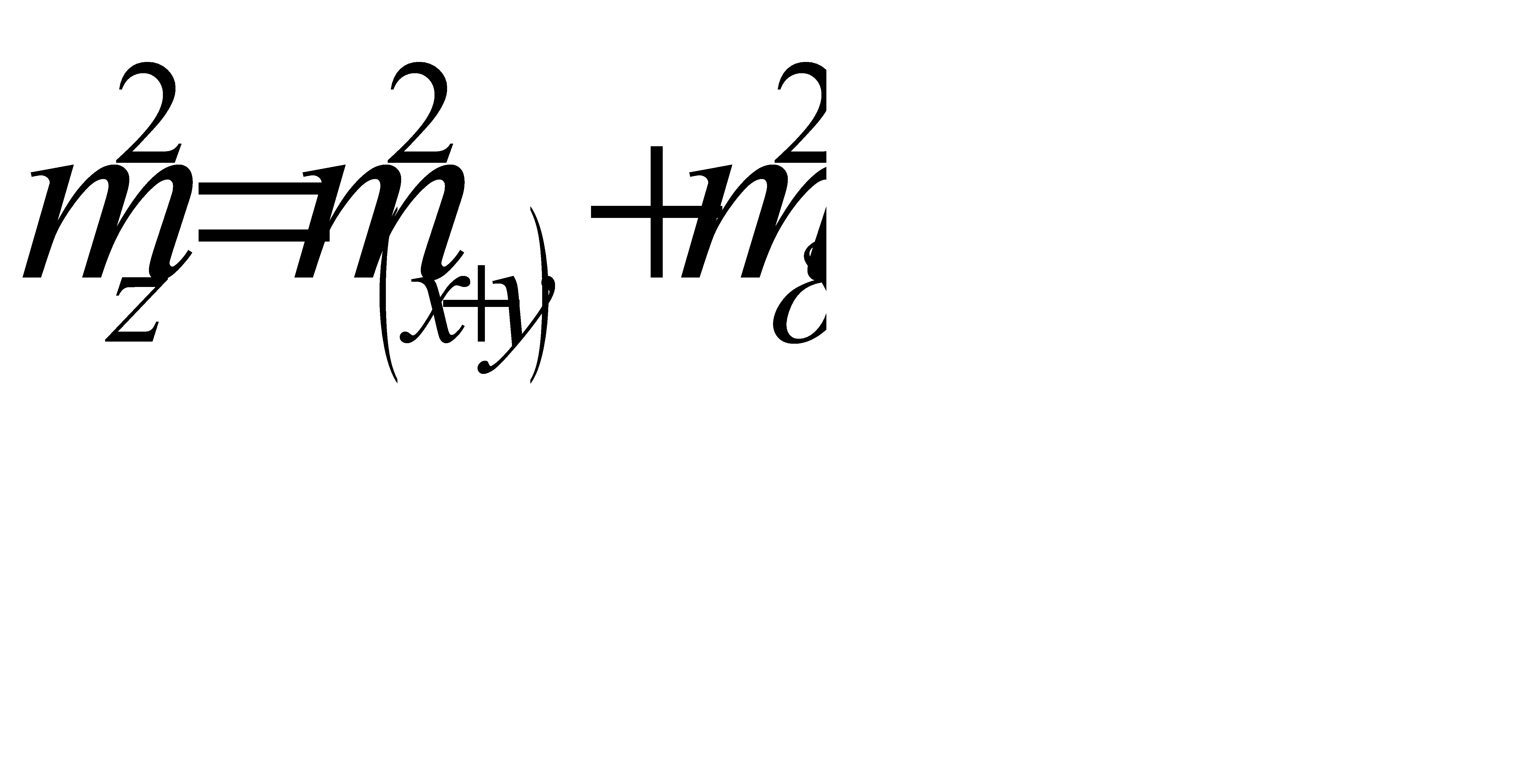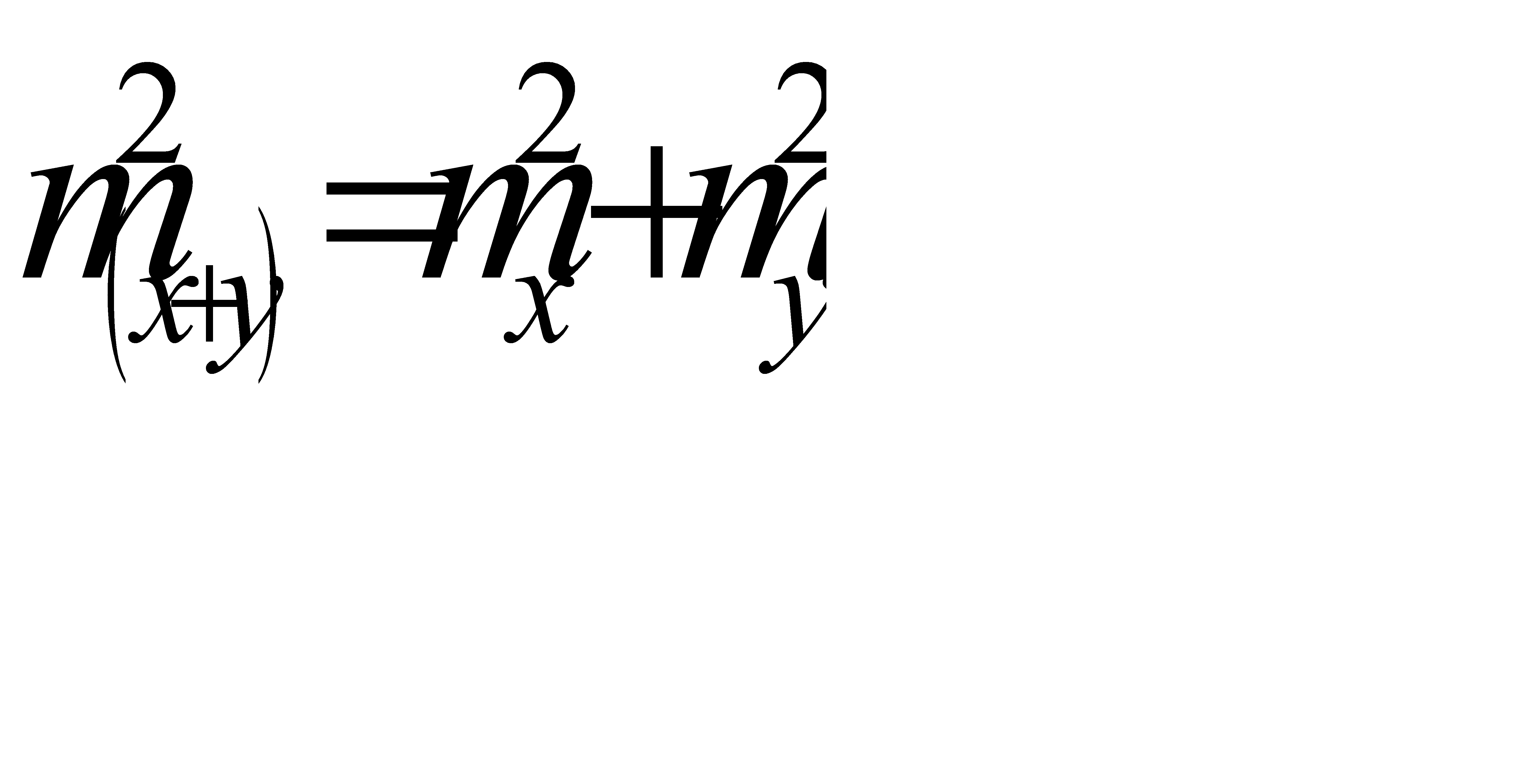Тогда можно записать: , но , поэтому .Если 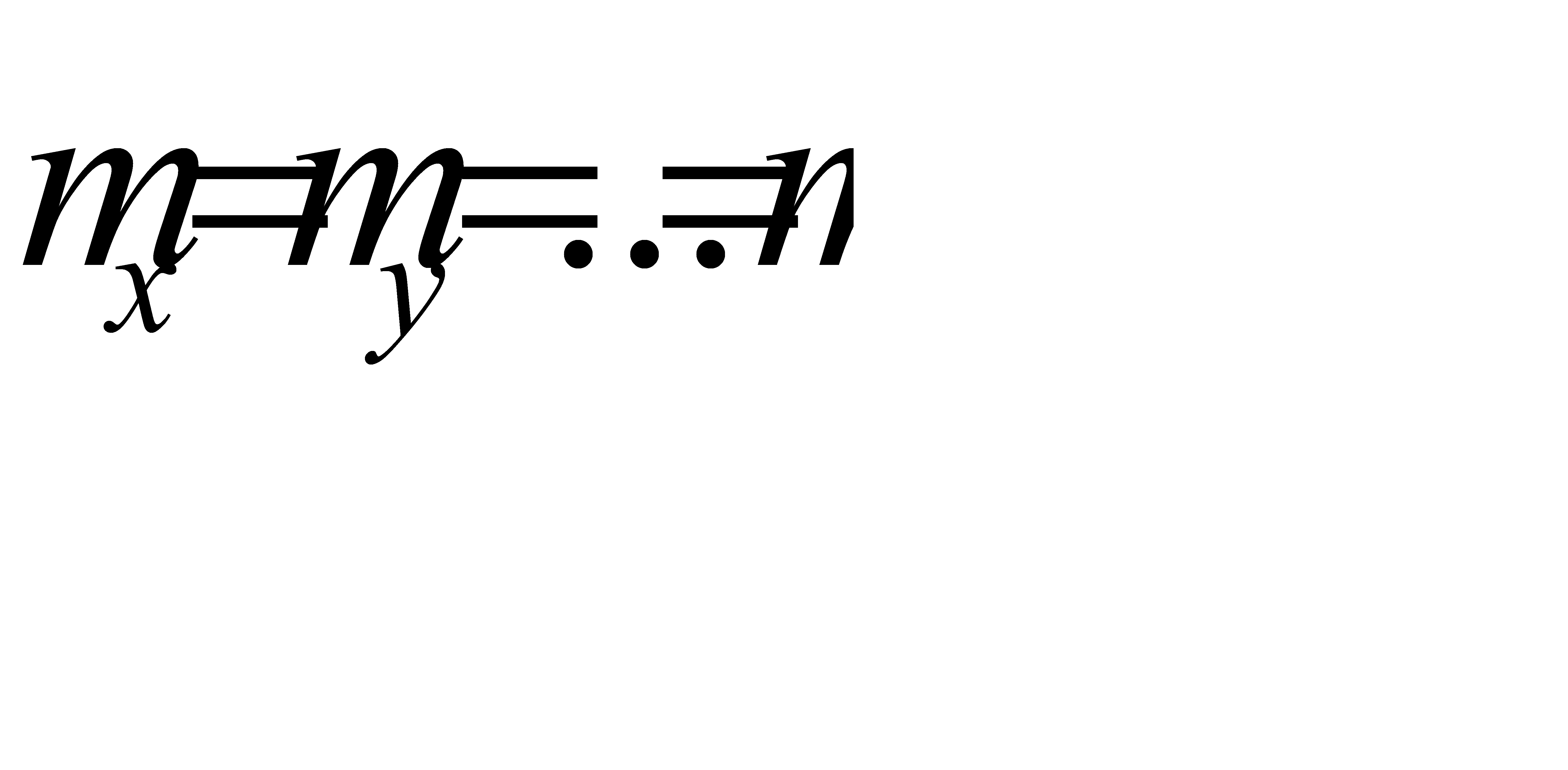, то при n слагаемых 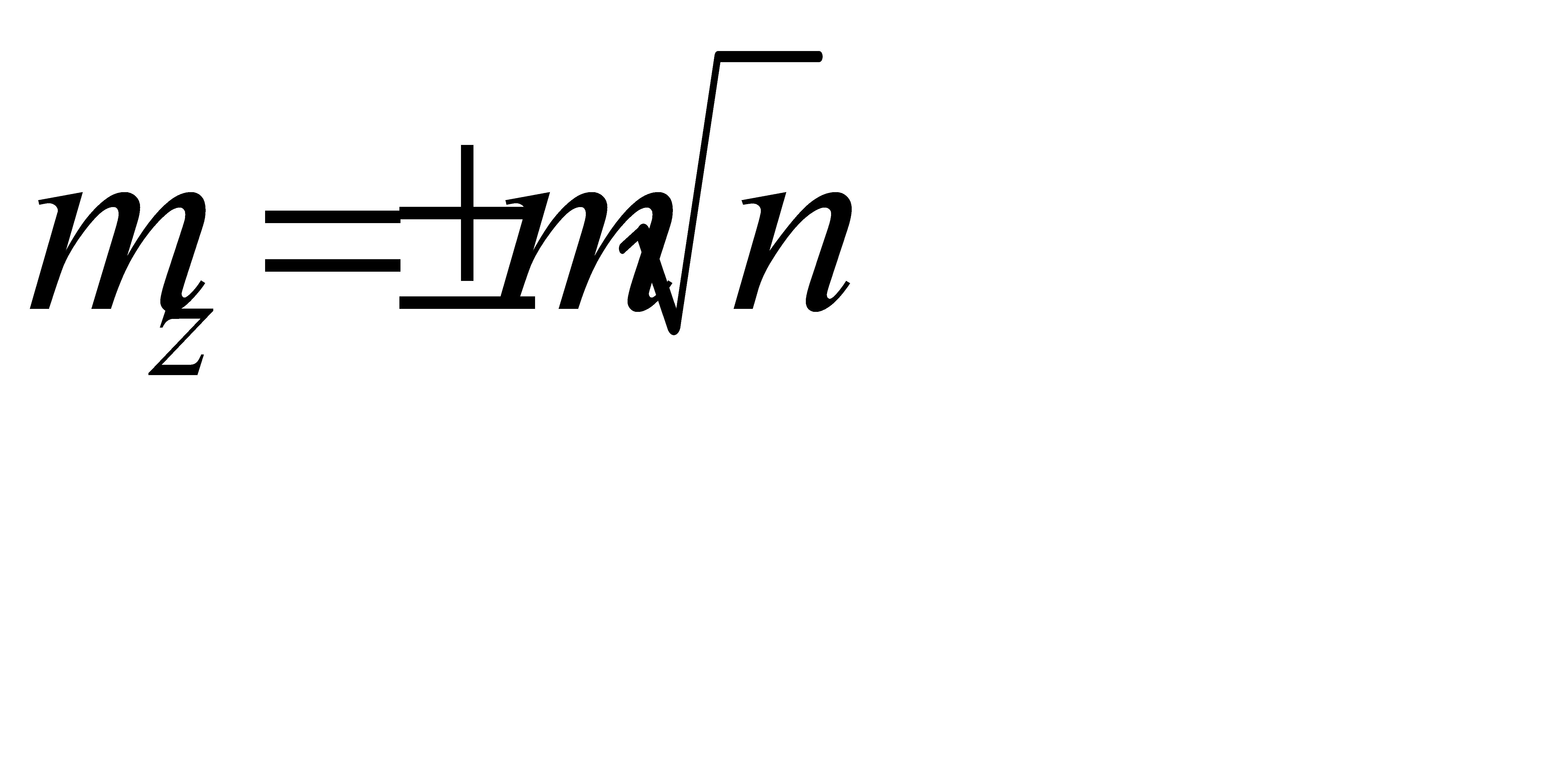, то есть квадрат средней квадратической ошибки суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.Средняя квадратическая ошибка алгебраической суммы измеренных с одинаковой точностью величин в 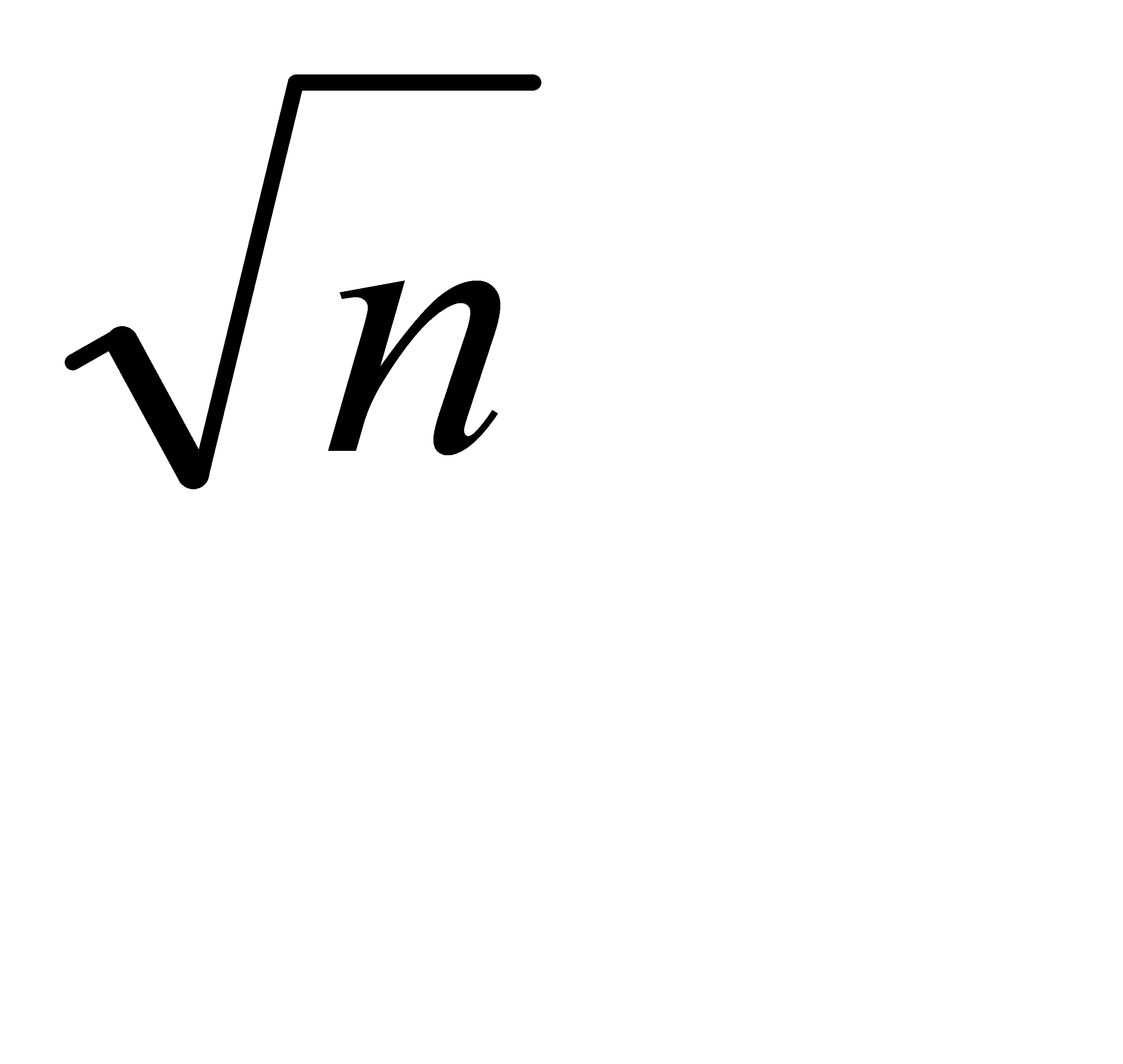раз больше средней квадратической ошибки одного слагаемого.

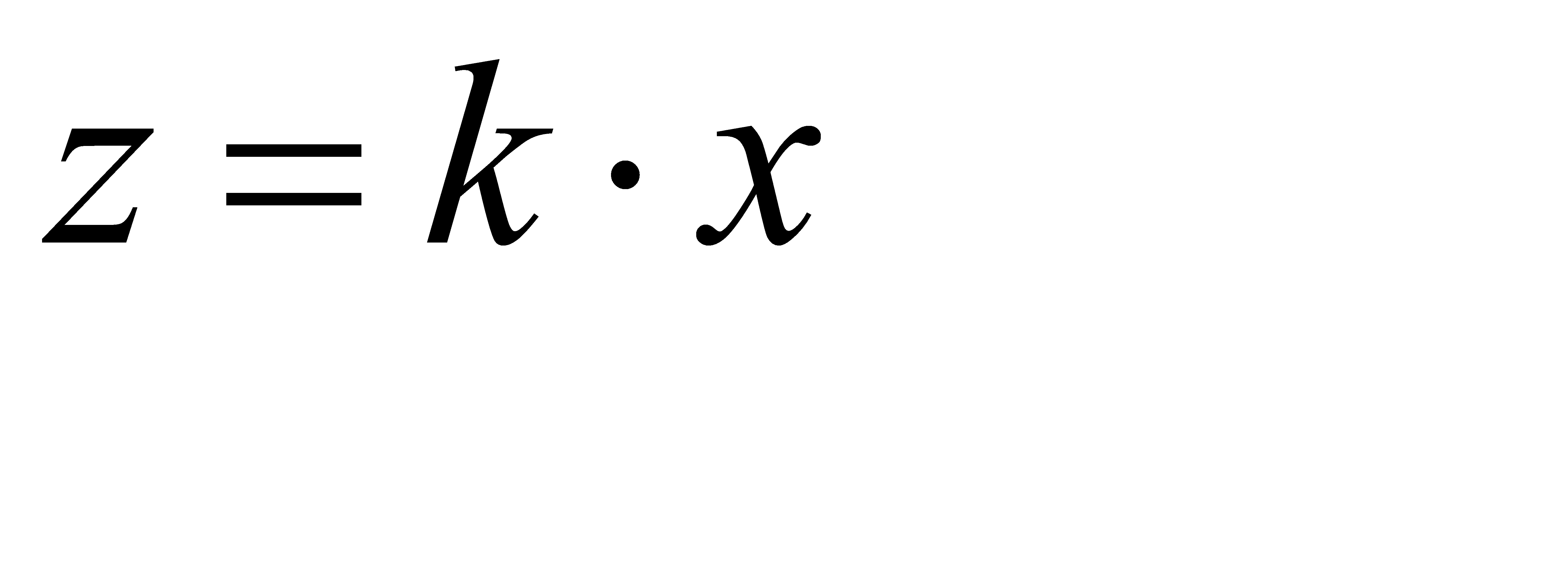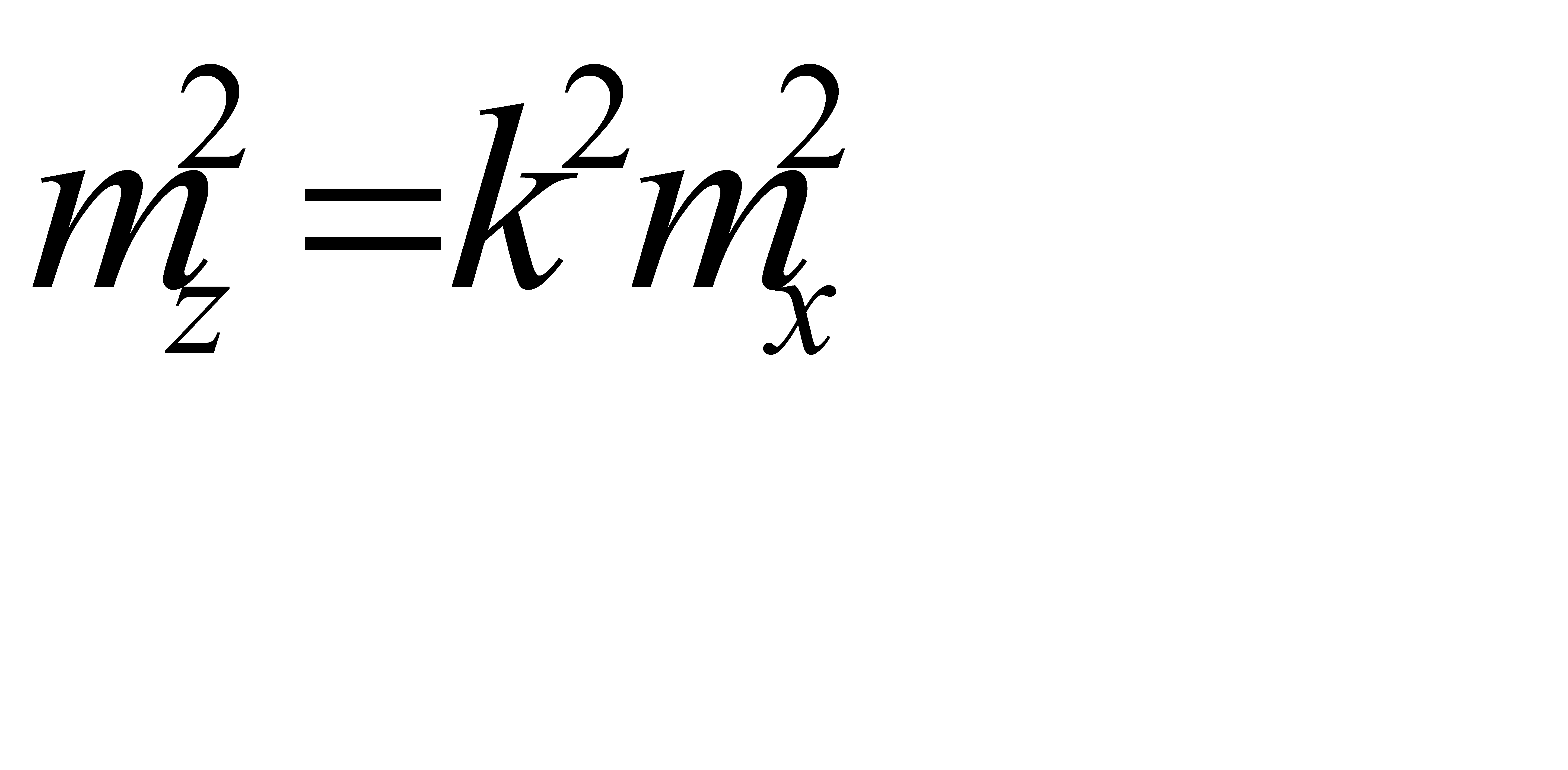49. Средняя квадратическая ошибка произведения постоянной величины на измеренную. Функция вида (произведения).k – постоянное число безошибочное.х – измерено несколько раз с ошибками ∆х₁, ∆х₂,… ∆х_n.; z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,…, ∆z_n. Отсюда или 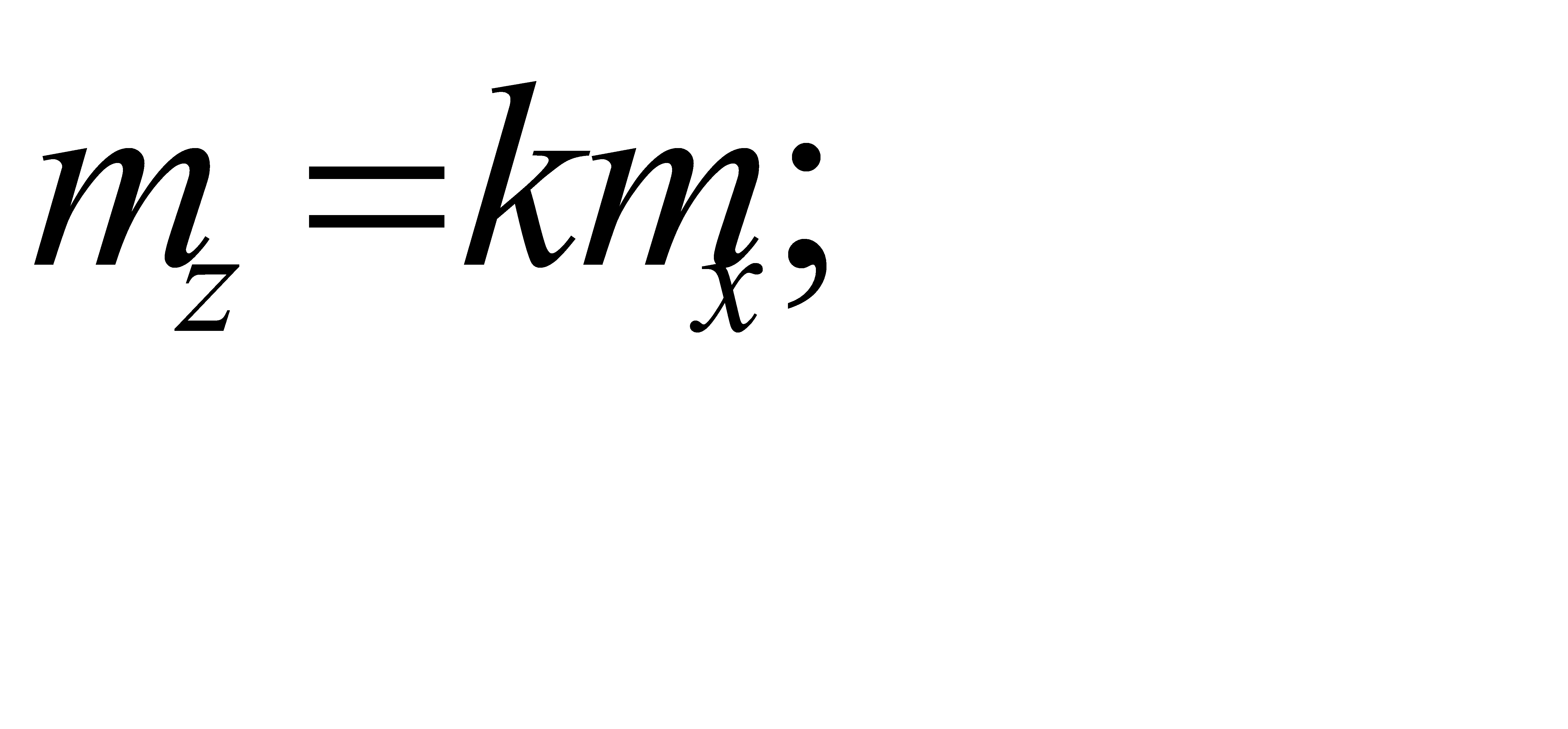,то есть средняя квадратическая ошибка произведения постоянного числа на аргумент равна произведению постоянного числа на среднюю квадратическую ошибку аргумента (измеряемой величины).